Тема 3. Второй закон термодинамики
Основные положения
Первый закон ТД утверждает, что теплота может превращаться в работу, а работа в теплоту, и не устанавливает условий, при которых возможны эти превращения.
Превращение работы в теплоту происходит всегда полностью и безусловно. Обратное превращение теплоты в работу при непрерывном её переходе возможно только при определенных условиях и не полностью.
Теплота сама собой переходит от более нагретых тел к холодным. От холодных тел к нагретым теплота сама собой не переходит. Для этого нужно затратить дополнительную энергию.
Второй закон термодинамики устанавливает, возможен или невозможен тот или иной процесс, в каком направлении протекает процесс, когда достигается ТД равновесие и при каких условиях можно получить максимальную работу.
Формулировки второго закона термодинамики. Для существования теплового двигателя необходимы два источника теплоты - горячий и холодный (окружающая среда). Если тепловой двигатель работает только от одного источника, то он называется вечным двигателем 2-го рода.
1. Формулировка Оствальда: "Вечный двигатель 2-го рода невозможен". Вечный двигатель 1-го рода - это тепловой двигатель, у которого L>Q 1, где Q 1 - подведенная теплота. Первый закон ТД "позволяет" создать тепловой двигатель, полностью превращающий подведенную теплоту Q 1 в работу L, т.е. L=Q 1. Второй закон накладывает более жесткие ограничения и утверждает, что работа должна быть меньше подведенной теплоты (L<Q 1) на величину отведенной теплоты Q 2, то есть
L = Q 1 - Q 2.
Вечный двигатель 2-го рода можно было бы осуществить, если бы теплоту Q 2 было возможно передать от холодного источника к горячему. Но для этого теплота самопроизвольно должна перейти от холодного тела к горячему, что невозможно.
2. Формулировка Клаузиуса: "Теплота не может самопроизвольно переходить от холодного тела к более нагретому".
Для работы теплового двигателя, как уже отмечалось, необходимы два источника - горячий и холодный.
3. Формулировка Карно: "Там, где есть разница температур, возможно совершение работы".
Все эти формулировки взаимосвязаны.
Формулировка Больцмана. Все естественные процессы являются переходом от менее вероятного состояния к более вероятному. Известно, что наиболее вероятным состоянием ТД системы является ТД равновесие.
Энтропия и энтальпия
Энтропия - величина, определяемая выражением
dS = dQ/T, [Дж/К]. (3.1)
Удельная энтропия:
ds=dq/ T, [Дж/(кг·К)]. (3.2)
Энтропия - однозначная функция состояния тела, принимающая для каждого состояния вполне определенное значение.
Энтропия - экстенсивный параметр состояния (зависит от массы вещества) - в любом ТД процессе полностью определяется начальным и конечным состоянием тела и не зависит от пути протекания процесса.
Энтропия как функция основных параметров состояния:
S=f 1(p, V); S=f 2(p, T); S=f 3(V, T); (3.3)
или, удельная энтропия:
s=f 1(p, v); s=f 2(p, T); S=f 3(v, T). (3.4)
Так как энтропия не зависит от вида процесса, то находят только её изменение в данном процессе по уравнениям:
Δ s = cv·ln (T 2/ T 1) + R·ln (v 2/ v 1); (3.5)
Δ s = cp·ln (T 2/ T 1) - R·ln (p 2/ p 1); (3.6)
Δ s = cv·ln (p 2/ p 1) + cр·ln (v 2/ v 1). (3.7)
Если к системе подводится тепло, то энтропия системы возрастает (Δ s >0). Если тепло от системы отводится, то энтропия системы уменьшается (Δs<0). Если тепло к системе не подводится и не отводится от неё (адиабатный процесс), то энтропия системы не изменяется (Δ s =0, s =const).
Энтальпия (теплосодержание) определяется как сумма внутренней энергии и работы расширения:
h = u + pv.
Цикл и теоремы Карно
Цикл Карно – круговой (замкнутый) цикл, состоящий из двух изотермических и двух адиабатных процессов. Обратимый цикл Карно в pv - и Ts -диа-граммах показан на рис.3.1. 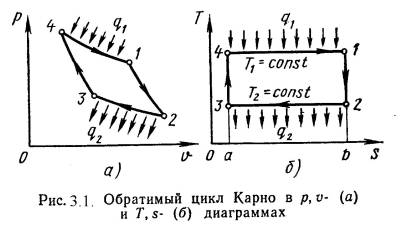
1-2 - обратимое адиабатное расширение, s 1=const. Температура снижается от Т 1 до Т 2.
2-3 - изотермическое сжатие, отвод теплоты q 2 к холодному источнику от рабочего тела.
3-4 - обратимое адиабатное сжатие, s 2=const. Температура повышается от Т 3 до Т 4.
4-1 - изотермическое расширение, подвод теплоты q 1 от горячего источника к рабочему телу.
Основная характеристика любого цикла - термический коэффициент полезного действия (т.кпд.):
ηt = Lц / Qц, (3.8)
Или
ηt = (Q 1– Q 2)/ Q 1.
Для обратимого цикла Карно т.кпд.:
ηtк =(Т 1– Т 2)/ Т 1. (3.9)
Отсюда следует 1-я теорема Карно: «Термический кпд обратимого цикла Карно не зависит от свойств рабочего тела и определяется только температурами источников».
Из сравнения произвольного обратимого цикла и цикла Карно вытекает 2-я теорема Карно: «Обратимый цикл Карно является наивыгоднейшим циклом в заданном интервале температур».
То есть т.кпд цикла Карно всегда больше т.кпд произвольного цикла:
η tк> η t. (3.10)
Тема 4. Термодинамические процессы






