Свободные колебания деформируемой системы с одной степенью свободы
Пусть на пружине с длиной L в ненагруженном состоянии подвешено тело массой m рассмотрим вертикальные движения теда после толчка под действием пружины и силы тяжести. Уравнение движения системы:
(II.7)
где fпр - восстанавливающая сила пружины, fтр - сила трения, Р - постоянная сила веса. По условию консервативности fтр=0 тогда величина fпр зависит только от ее деформации - координаты х1. Между силой и деформацией пружины существует линейная зависимость - закон Гука fпр = fпр(x0) + k(x1 – x0)
Выберем новую координату х=х1-х0, это означает, что начало отсчета системы координат перемещается в положение равновесия, где fпр(х0)=Р. Тогда уравнение (II.7) запишется так (II.8)
или (II.9)
где ω2=k/m. Таким образом, ω2 - единственный физический параметр, характеризующий колебательные свойства системы. Решение дифференциального уравнения (II.9):
х =А cosωt + B sin ωt (II.10)
где А и В- постоянные величины, зависящие от начальных условий. Отклонение от положения равновесия будет совершать со времена гармонические колебания с частотой ω. Эти колебания называются собственными (или свободными) колебаниями.
Продолжительность одного цикла колебаний - период колебаний Т=2π/ω или
(II.11)
измеряется в сек. Величину (II.12) называют круговой собственной частотой системы в отличии от обычной частоты р, равной числу периодов колебаний за единицу времени. Частота р=1/Т измеряется в герцах. Период свободных колебаний Т и связанная с ним частота являются главнейшими динамическими параметрами системы (конструкции, сооружения). Величину k называют жесткостью системы или коэффициентом жесткости (н/м, дин/см, кгс/см и т.д.) Величина k равна силе, которую нужно приложить к пружине, чтобы изменить ее деформацию на единицу длины.
Следовательно, период колебаний зависит от отношения массы и жесткости системы. Свободные колебания с течением времени затухают от сопротивления внешнего и внутреннего трения. При механических колебаниях трение пропорционально первой степени скорости. Уравнение движения (II.8) примет вид:
(II.13)
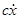
где - сила трения, С - коэффициент силы трения, имеющий размерность Н
сек/м или кгс сек/м.
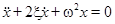Для анализа колебательного процесса уравнение (II.13) можно представить в виде:
(II.14)
где ξ=C/2m и ω2= k/m (II.15)
Размерность |ξ|= сек-1. Уравнение (II.14) является уравнением затухающих колебаний системы его решение имеет вид:
x = D eξt cos(ωD t - α) (II.16)
где D и α - константы, зависящие от начальных условий, а ω2D= ω2- ξ2 (II.17)
На рис. внизу затухающие колебания одномассовой системы
