Модуль реальная математика

ПОДГОТОВКА К ЭКЗАМЕНАМ

ТЕСТ 1 (Октябрь)

МОДУЛЬ АЛГЕБРА

1. Рас­по­ло­жи­те в по­ряд­ке воз­рас­та­ния: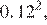

 

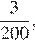
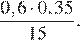
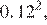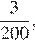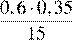
1)	2)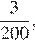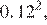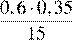
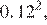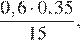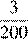
3)	4)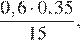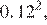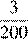

2. На ко­ор­ди­нат­ной пря­мой от­ме­че­но число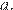

 

Рас­по­ло­жи­те в по­ряд­ке воз­рас­та­ния числа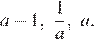

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

 

1)

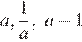
2)

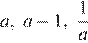
3)

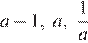
4)

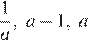
3. Най­ди­те зна­че­ние вы­ра­же­ния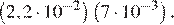

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

 

1) 0,00154

2) 15400000

3) 0,000154

4) 0,0000154

 

Ре­ши­те урав­не­ние

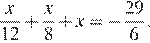
Уста­но­ви­те со­от­вет­ствие между гра­фи­ка­ми функ­ций и фор­му­ла­ми, ко­то­рые их за­да­ют.

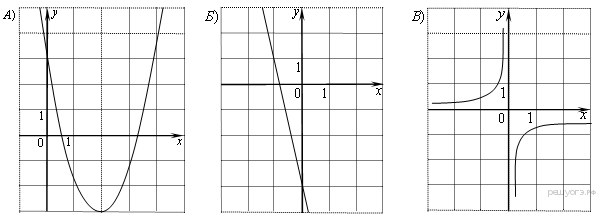
1)

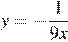
2)

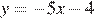
3)

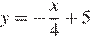
4)

 

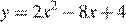
Ответ ука­жи­те в виде по­сле­до­ва­тель­но­сти цифр без про­бе­лов и за­пя­тых в ука­зан­ном по­ряд­ке

 

А	Б	В

 

6. По­сле­до­ва­тель­ность за­да­на фор­му­лой 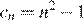. Какое из ука­зан­ных чисел яв­ля­ет­ся чле­ном этой по­сле­до­ва­тель­но­сти?

 

1) 1

2) 2

3) 3

4) 4

Най­ди­те зна­че­ние вы­ра­же­ния

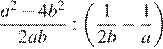, при , .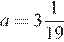

 

 

8. Ре­ше­ние ка­ко­го из дан­ных не­ра­венств изоб­ра­же­но на ри­сун­ке?

 

 

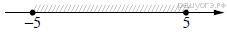
1)

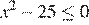
2)

3)

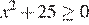
4)

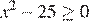
МОДУЛЬ ГЕОМЕТРИЯ

9. На про­дол­же­нии сто­ро­ны AD па­рал­ле­ло­грам­ма ABCD за точ­кой D от­ме­че­на точка E так, что DC = DE. Най­ди­те боль­ший угол па­рал­ле­ло­грам­ма ABCD, если ∠ DEC = 27°. Ответ дайте в гра­ду­сах.

10. В окруж­ность впи­сан рав­но­сто­рон­ний вось­ми­уголь­ник. Най­ди­те ве­ли­чи­ну угла ABC.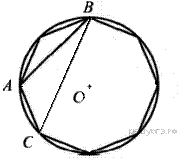

11. Ос­но­ва­ния тра­пе­ции равны 18 и 12, одна из бо­ко­вых сто­рон равна 6, а тан­генс угла между ней и одним из ос­но­ва­ний равен 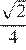. Най­ди­те пло­щадь тра­пе­ции.

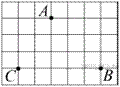
12. На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см × 1 см от­ме­че­ны точки А, В и С. Най­ди­те рас­сто­я­ние от точки А до пря­мой BC. Ответ вы­ра­зи­те в сан­ти­мет­рах

13. Какие из дан­ных утвер­жде­ний верны? За­пи­ши­те их но­ме­ра.

 

1) Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой на­крест ле­жа­щие углы равны, то пря­мые па­рал­лель­ны.

2) Диа­го­наль тра­пе­ции делит её на два рав­ных тре­уголь­ни­ка.

3) Если в ромбе один из углов равен 90°, то такой ромб — квад­рат.

 

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.

МОДУЛЬ РЕАЛЬНАЯ МАТЕМАТИКА

14. На диа­грам­ме по­ка­за­но ко­ли­че­ство школь­ни­ков, по­се­тив­ших те­ат­ры г. Крас­но­да­ра за 2010 г. Опре­де­ли­те, сколь­ко при­мер­но зри­те­лей по­се­ти­ли за этот пе­ри­од Фи­лар­мо­нию, если во всех этих те­ат­рах школь­ни­ков было 2000 че­ло­век.

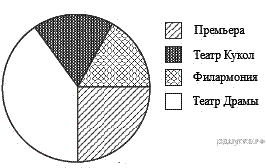
В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

 

1) 150

2) 240

3) 350

4) 500

15. На гра­фи­ках по­ка­за­но, как во время те­ле­ви­зи­он­ных де­ба­тов между кан­ди­да­та­ми А и Б те­ле­зри­те­ли го­ло­со­ва­ли за каж­до­го из них. Сколь­ко всего те­ле­зри­те­лей про­го­ло­со­ва­ло к 40-й ми­ну­те де­ба­тов?

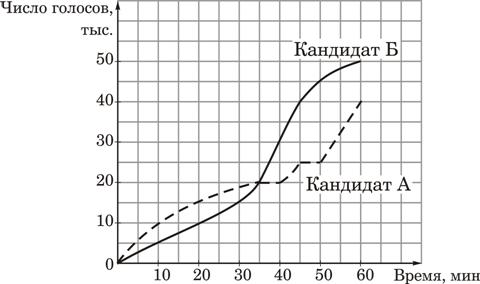
16. По­сту­пив­ший в про­да­жу в ян­ва­ре мо­биль­ный те­ле­фон стоил 2400 руб­лей. В но­яб­ре он стал сто­ить 1200 руб­лей. На сколь­ко про­цен­тов сни­зи­лась цена на мо­биль­ный те­ле­фон в пе­ри­од с ян­ва­ря по но­ябрь?

 

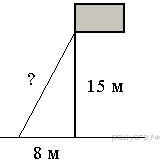
17. Точка креп­ле­ния троса, удер­жи­ва­ю­ще­го флаг­шток в вер­ти­каль­ном по­ло­же­нии, на­хо­дит­ся на вы­со­те 15 м от земли. Рас­сто­я­ние от ос­но­ва­ния флаг­што­ка до места креп­ле­ния троса на земле равно 8 м. Най­ди­те длину троса.

 

 

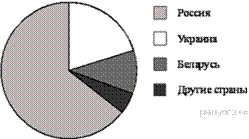
18. На диа­грам­ме пред­став­ле­но рас­пре­де­ле­ние ко­ли­че­ства поль­зо­ва­те­лей не­ко­то­рой со­ци­аль­ной сети по стра­нам мира. Всего в этой со­ци­аль­ной сети 9 млн поль­зо­ва­те­лей.

Какое из сле­ду­ю­щих утвер­жде­ний не­вер­но?

 

1) Поль­зо­ва­те­лей из Бе­ла­ру­си мень­ше, чем поль­зо­ва­те­лей из Укра­и­ны.

2) Поль­зо­ва­те­лей из Укра­и­ны боль­ше чет­вер­ти об­ще­го числа поль­зо­ва­те­лей.

3) Поль­зо­ва­те­лей из Бе­ла­ру­си боль­ше, чем поль­зо­ва­те­лей из Фин­лян­дии.

4) Поль­зо­ва­те­лей из Рос­сии боль­ше 4 мил­ли­о­нов.

 

19. Стре­лок три раза стре­ля­ет по ми­ше­ням. Ве­ро­ят­ность по­па­да­ния в ми­шень при одном вы­стре­ле равна 0,7. Най­ди­те ве­ро­ят­ность того, что стре­лок пер­вые два раза попал в ми­ше­ни, а по­след­ний раз про­мах­нул­ся.

 

20. За 20 минут ве­ло­си­пе­дист про­ехал 7 ки­ло­мет­ров. Сколь­ко ки­ло­мет­ров он про­едет за t минут, если будет ехать с той же ско­ро­стью? За­пи­ши­те со­от­вет­ству­ю­щее вы­ра­же­ние.

ЧАСТЬ II

(ВСЕ ЗАДАНИЯ РЕШАЮТСЯ С ПОЛНЫМ ОБОСНОВАНИЕМ)

21. Упро­сти­те вы­ра­же­ние: .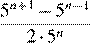

22. Теп­ло­ход про­хо­дит по те­че­нию реки до пунк­та на­зна­че­ния 165 км и после сто­ян­ки воз­вра­ща­ет­ся в пункт от­прав­ле­ния. Най­ди­те ско­рость теп­ло­хо­да в не­по­движ­ной воде, если ско­рость те­че­ния равна 4 км/ч, сто­ян­ка длит­ся 5 часов, а в пункт от­прав­ле­ния теп­ло­ход воз­вра­ща­ет­ся через 18 часов после от­плы­тия из него.

23. По­строй­те гра­фик функ­ции

 

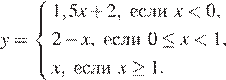
и опре­де­ли­те, при каких зна­че­ни­ях 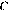пря­мая имеет с гра­фи­ком ровно две общие точки.

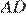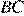24. Каж­дое ос­но­ва­ние и тра­пе­ции 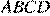про­дол­же­но в обе сто­ро­ны. Бис­сек­три­сы внеш­них углов 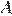и 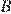этой тра­пе­ции пе­ре­се­ка­ют­ся в точке 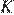, бис­сек­три­сы внеш­них углов и 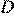пе­ре­се­ка­ют­ся в точке 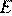. Най­ди­те пе­ри­метр тра­пе­ции 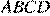, если длина от­рез­ка 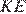равна 28.

25. В па­рал­ле­ло­грам­ме про­ве­де­ны бис­сек­три­сы про­ти­во­по­лож­ных углов. До­ка­жи­те, что от­рез­ки бис­сек­трис, за­клю­чен­ные внут­ри па­рал­ле­ло­грам­ма, равны.

26. Окруж­ность ра­ди­у­са 4 ка­са­ет­ся внеш­ним об­ра­зом вто­рой окруж­но­сти в точке . Общая ка­са­тель­ная к этим окруж­но­стям, про­хо­дя­щая через точку 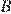, пе­ре­се­ка­ет­ся с не­ко­то­рой дру­гой их общей ка­са­тель­ной в точке 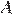. Най­ди­те ра­ди­ус вто­рой окруж­но­сти, если .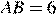