| Вид преобразования | Пункты меню Symbolics | Описание |
| Упрощение | Simplify | Упростить выражение с выполнением таких операций, как сокращение подобных слагаемых, приведение к общему знаменателю, использование основных тригонометрических тождеств и т. д. |
| Расширение | Expand | Раскрыть выражение (раскрываются суммы и произведения, тригонометрические функции разлагаются по тригонометрическим тождествам). |
| Разложение на множители | Factor | Разложить число или выражение на простые множители. |
| Приведение подобных слагаемых | Collect | Привести подобные слагаемые полинома. |
| Коэффициенты полинома | Coeffs | Определить коэффициенты полинома относительно указанной переменной. |
| Разложение на элементарные дроби | Partfrac | — |
| Разложение в ряд Тейлора | Series | — |
| Преобразование Лапласа | Laplace | — |
| Обратное преобразование Лапласа | Invlaplace | — |
| Преобразование Фурье | Fourier | — |
| Обратное преобразование Фурье | Invfourier | — |
Символьная операция Simplify (Упростить) — одна из самых важных. Эта операция позволяет упрощать математические выражения, содержащие алгебраические и тригонометрические функции, а также выражения со степенными многочленами (полиномами). Упрощение означает замену более сложных фрагментов выражений на более простые. Приоритет тут отдается простоте функций. К примеру, функция tan(x) считается более сложной, чем функции sin(x) и cos(x). Поэтому tan(x) упрощается так, что получает представление через соотношение этих функций.
Эта команда открывает широкие возможности для упрощения сложных и плохо упорядоченных алгебраических выражений. На рис. 2 даны примеры применения операции Simplify.

Рис. 2.
Система Mathcad содержит встроенную функцию для вычисления значений определенных интегралов приближенным численным методом. Ею целесообразно пользоваться, когда нужно просто получить значение определенного интеграла в виде числа.
Однако команда Simplify применительно к вычислениям определенных интегралов делает гораздо больше — она ищет аналитическое выражение для интеграла. Более того, она способна делать это и при вычислении кратных интегралов, пределы которых — функции. Наглядный пример этому продемонстрирован на рис. 3.
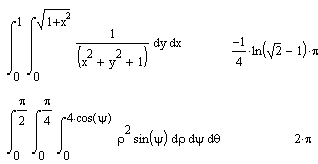
Рис. 3.
Операцию Simplify можно использовать и для вычисления сумм и произведений символьных последовательностей. Результат операции, как и следовало ожидать, получается в символьной форме (если она существует) (рис. 4).
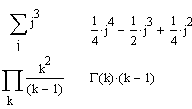
Рис. 4.
Приведенные примеры могут создать впечатление, что Mathcad лихо справляется со всеми производными, интегралами, суммами и произведениями с помощью операции Simplify. К сожалению, это далеко не так. Нередко система не справляется с кажущимися простыми справочными примерами. Надо помнить, что символьный процессор системы Mathcad обладает заметно урезанной библиотекой функций и преобразований (в сравнении с библиотекой системы Maple V). Поэтому часто система не находит решение в замкнутом виде, хотя оно и приводится в справочнике. Тогда система повторяет введенное выражение или сообщает об ошибке.
В результате преобразований могут появляться специальные функции — как встроенные в систему (функции Бесселя, гамма-функция, интеграл вероятности и др.), так и ряд функций, дополнительно определенных при загрузке символьного процессора (интегральные синус и косинус, интегралы Френеля, эллиптические интегралы и др.). Последние нельзя использовать при создании математических выражений.
Действие операции Expand (Разложить по степеням) в известном смысле противоположно действию операции Simplify. Подвергаемое преобразованию выражение расширяется с использованием известных (и введенных в символьное ядро) соотношений, например алгебраических разложений многочленов, произведений углов и т. д. Разумеется, расширение происходит только в том случае, когда его результат однозначно возможен. Иначе нельзя считать, что действие этой операции противоположно действию операции Simplify. К примеру, операция Simplify преобразует сумму квадратов синуса и косинуса в 1, тогда как обратное преобразование многозначно и потому в общем виде невыполнимо.
При преобразовании выражений операция Expand старается более простые функции представить через более сложные, свести алгебраические выражения, представленные в сжатом виде, к выражениям в развернутом виде и т. д. Примеры действия операции Expand даны на рис. 5.

Рис. 5.
Последний пример показывает, что результатом операции может быть специальная математическая функция, которая считается более сложным выражением, чем порождающее ее выражение. С виду, однако, выражения со специальными математическими функциями обычно выглядят гораздо проще, чем исходные выражения.
Операция Factor (Разложить на множители) используется для факторизации — разложения выражений или чисел на простые множители. Она способствует выявлению математической сущности выражений; к примеру, наглядно выявляет представление полинома через его действительные корни, а в том случае, когда разложение части полинома содержит комплексно-сопряженные корни, порождающее их выражение представляется квадратичным трехчленом. Примеры действия этой операции даны на рис. 6.

Рис. 6.
В большинстве случаев (но не всегда) операция факторизации ведет к упрощению выражений. Термин «факторизация» не является общепризнанным в отечественной математической литературе, но мы его оставляем в связи с созвучностью с англоязычным именем этой операции.
Операция Collect (Разложить по подвыражению) обеспечивает замену указанного выражения выражением, скомплектованным по базису указанной переменной, если такое представление возможно (рис. 7). В противном случае появляется окно с сообщением о невозможности комплектования по указанному базису.

Рис. 7.
Эта команда особенно удобна, когда заданное выражение есть функция ряда переменных и нужно представить его в виде функции заданной переменной имеющей вид степенного многочлена. При этом другие переменные входят в сомножители указанной переменной, представленной в порядке уменьшения ее степени.
Операция Polynomial Coefficients (Полиномиальные коэффициенты) служит для вычисления коэффициентов полинома. Операция применяется, если заданное выражение – полином (степенной многочлен) или может быть представлено таковым относительно выделенной переменной. Результатом операции является вектор с коэффициентами полинома (рис. 8).

Рис. 8.






