Описание функций
В среде MuPAD функции можно задавать несколькими способами. Рассмотрим самый простой - с помощью оператора «стрелка» (оператор ->).
При описании функции соблюдается следующая последовательность ввода:
· имя функции;
· оператор присваивания (:=);
· список аргументов (разделенных запятыми);
· оператор «стрелка» (->);
· выражение, в которое входят аргументы, представляющее собой функциональную зависимость.
На рис. 5 приведено описание и получение числового значения функции 
при х=2. Здесь y определяется как оператор, который действуя на переменную х, вычисляет значение x^2, а переменная х играет роль формального параметра. Как показано на рис. 3.4-5 функцию, объявленную таким способом, можно использовать при расчетах в разных выражениях, а также при построении графиков.
Рис. 3.4-5 Описание функции от одной переменной
При объявлении функции от двух переменных, как показано на рис. 3.4-6, аргументы вводятся через запятую, и заключены в скобки. Аналогично предыдущему примеру, после нажатия клавиши <Enter> в следующей строке появляется символьное выражение функциональной зависимости. Ниже показана возможность использования объявленной двумерной функции при построении графика. Использование в команде plot() вместо переменных х и y переменные хх и yy, показывает, что аргументы при описании функции также играют роль формальных параметров.
Рис. 3.4-6. Описание функции от двух переменных
Вычисление производных
Производные в MuPAD, также как и в MatLAB, вычисляются с помощью функции diff(). Дифференцируемое выражение указывается первым аргументом функции, а переменная, по которой происходит дифференцирование – вторым. Функцию diff() можно ввести с клавиатуры, а можно воспользоваться значком, изображающим производную.
Дифференцируемое выражение может быть непосредственно указано в функции diff(), как например, в команде diff(x^2*sin(x), x), или объявлено перед использованием функции. После нажатия клавиши <Enter> в следующей строке появляется символьное выражение производной (рис.3.4-7).
Функция diff() вычисляются производные и высших порядков. В общем случае переменные, по которым вычисляются производные от выражения, являющимся первым аргументом, указываются через запятую в соответствии с порядком вычисления производной. В нашем случае переменная дифференцирования одна, следовательно, для получения второй производной, через запятую указывается та же переменная х, а для третьей производной – еще один х.
Следует отметить, что результат вычисления производной очень часто представлен в неупрощенном виде. Для упрощения выражения используется функция simplify(), аргументом которой служит упрощаемое выражение. Если, как в нашем случае, упрощения требует результат предыдущей команды, то в качестве ссылки используется инструкция % (рис. 3.4-7).
Рис.3.4-7. Вычисление производных
При работе с функцией от одной переменной производную можно вычислить также с помощью оператора производной – штриха (знак апостроф ‘) или с помощью функции D(). Примеры использования этих операторов приведены в нижней части рис.7. Чтобы с использованием оператора штрих вычислить производную высшего порядка оператор штрих указывается несколько раз (например, f’’(t) – производная 2-го порядка). При вычислении производная 2-го порядка с использованием функции D(), следует ввести D(@@2) (f) (t). Если вместо переменной t задать числовое значение (например, D(@@2)(f) (5), то вычисляется значение производная 2-го порядка при значении t=2.
Достаточно просто в MuPAD вычисляются и частные производные. В этом случае применяются функция diff() или D().
На рис.3.4-8 показан процесс вычисления частных производных от функции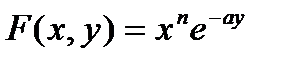 
. Функция описана с использованием оператора «стрелка» и получено ее символьное выражение, а затем приведены примеры вычисления частных производных по двум аргументам с использованием функции diff() и частных производных по первой переменной и по второй переменной с использованием функции D().
Рис.3.4-8. Вычисление производных
Вычисление интегралов
Интегралы в MuPAD вычисляются с использованием функции int(). Первым аргументом указывается подынтегральное выражение, а вторым – переменная интегрирования. На рис.9 приведены примеры вычисления неопределенных и определенных интегралов (ключевым словом infinity обозначается бесконечность), получение интеграла в аналитическом аналитического выражения и его числового значения, для чего функцию int() пришлось дополнить внешней функцией float().
К сожалению не любой интеграл может быть представлен в аналитическом виде, как показано на рис.3.4-9. В таком случае можно прибегнуть к вычислению интеграла в числовом виде. При использовании команды float(int(exp(-x)*cos(5*x),x=0..infinity)) вычислить интеграл в символьном виде не удается, поэтому на экран выдается его числовое значение. Команда numeric::int(sin(2*PI*x)/sqrt(1+x),x=0..1) сразу использует числовой алгоритм.
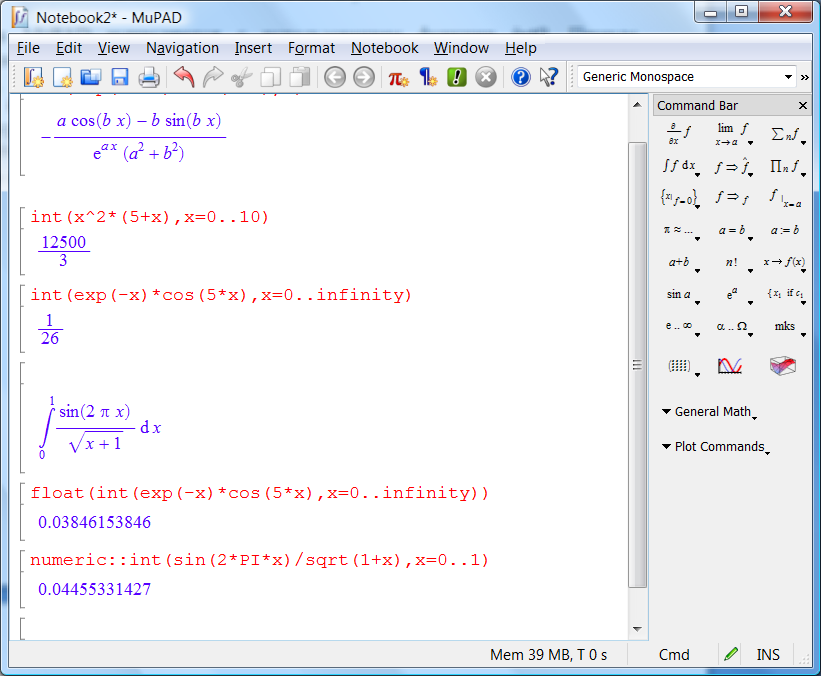
Рис. 3.4-9. Вычисление интегралов
