1. Цель работы: закрепление теоретических знаний по теме 1.3. “Удар”,
приобретение практических навыков в измерении линейных и угловых величин, в работе с баллистическим гальванометром,
изучение методики расчетов физических величин при ударе.
2. Порядок подготовки к выполнению работы изучить тему и материал лабораторной работы
3. Порядок выполнения лабораторной работы
4. Подведение итогов выполнения работы предъявить результаты,
подготовка и оформление отчета, заполнить таблички, произвести обработку результатов измерений
5. техника безопасности при выполнении лабораторной работы
Принадлежности: установка, секундомер, линейка
Теория. Отношение относительной скорости тел после удара u1 - u2 к относительной скорости до удара v1 - v2 называется коэффициентом восстановления 1):
k=  . (1)
. (1)
В условиях опыта коэффициент восстановления может считаться величиной, зависящей только от материала соударяющихся тел. Величину к о э ф ф и ц и е н т а в о с с т а н о в л е н и я и времени соударения удобно определять при центральном ударе шаров.
Пусть два шара одинаковой массы висят на нитях равной длины, касаясь друг друга. Если оба шара отклонить на равные углы и одновременно освободить их, то они, сталкиваясь друг с другом, в любой момент времени будут иметь скорости, равные по величине, но разные по знаку. Коэффициент восстановления в этом случае равен
k =  ,
,
где u - скорость шара (любого) после удара, v - скорость шара до удара.
Для n последовательных соударений может быть написано n уравнений:
u1 = kv1,
u2 = kv2.............. (2)
un = kvn.
Пользуясь тем, что u1 = v2, u2 = v3,...( пренебрегая силами трения), из уравнений (2) получаем
kn =  . (3)
. (3)
Отношение скоростей может быть заменено отношением расстояний (дуг), проходимых шарами. Если шар опускается по вертикали на высоту h, то скорость v может быть представлена в виде
v = 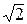 gh, (4)
gh, (4)
где g - ускорение силы тяжести.
Пусть l - длина нити подвеса шара,  - угол отклонения шара, s - расстояние, проходимое шаром. Тогда
- угол отклонения шара, s - расстояние, проходимое шаром. Тогда
 , h= l (1 - cos
, h= l (1 - cos  ) = 2l sin2
) = 2l sin2  .
.
При l >>  s из этих уравнений получаем
s из этих уравнений получаем
h=  . (5)
. (5)
Уравнения (3) - (5) дают
k = (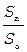 ) 1/n (6)
) 1/n (6)
где S0 - расстояние (дуга), проходимое шаром до первого соударения, S n - расстояние, проходимое шаром после n-го удара.
Формула (6) получена в предположении, что сил трения нет. В действительности имеет место сила трения шаров о воздух, что приводит
к уменьшению амплитуды каждого последующего колебания даже при отсутствии соударений (т.е. при колебании одного шара). Закон убывания амплитуды может быть представлен в виде
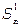 = qn S0 (7)
= qn S0 (7)
где 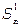 - амплитуда n-го неполного колебания, q - некоторая константа, несколько меньшая единицы. Закон убывания амплитуды может быть проверен экспериментально, так как согласно (7) должны выполняться соотношения
- амплитуда n-го неполного колебания, q - некоторая константа, несколько меньшая единицы. Закон убывания амплитуды может быть проверен экспериментально, так как согласно (7) должны выполняться соотношения

В процессе колебаний с соударениями уменьшение амплитуды происходит не только в результате действия сил трения, но также и вследствие неполного восстановления скорости при соударении. Так как амплитуда пропорциональна скорости в нижней точке, то S1 = kqS0, откуда Sn = kn qn S0 = kn S’n, т.е. для определения коэффициента восстановления получаем следующую формулу, учитывая силу трения:
k =( .
. 
 (8)
(8)
В р е м я с о у д а р е н и я зависит от относительной скорости шаров в момент удара, упругих постоянных для их материала, а также радиуса шаров.
Если шары соединить проводником с заряженным конденсатором, то в течение времени соударения шаров конденсатор будет разряжаться. Время соударения может быть поэтому отождествлено со временем разрядки конденсатора. Конденсатор разряжается по закону
Q (t) = Q0  , (9)
, (9)
где С - емкость конденсатора, R - сопротивление цепи при разрядке, t - время после разрядки, Q (t) - заряд, оставшийся на конденсаторе к моменту времени t. Q0 - начальный заряд на конденсаторе.
В нашем случае в момент времени t =  процесс разрядки прерывается, поэтому время соударения
процесс разрядки прерывается, поэтому время соударения  равно
равно
 = Rc l n
= Rc l n  , (10)
, (10)
где Q - заряд, оставшийся на конденсаторе после соударения.
Для измерения величины заряда пользуются баллистическим гальванометром (см.задачу 84, тП), отклонение рамки которого пропорционально величине заряда. Величины зарядов пропорциональны, таким образом, смещениям “зайчика” по шкале прибора
Q0 =  n0 и Q =
n0 и Q =  n,
n,
где  - коэффициент пропорциональности, n0 и n - деления шкалы. Пользуясь этими соотношениями, получаем окончательно
- коэффициент пропорциональности, n0 и n - деления шкалы. Пользуясь этими соотношениями, получаем окончательно
 = Rc l n
= Rc l n  (11)
(11)
Этой зависимостью и пользуются в настоящей задаче при измерении времени соударения.
Описание установки. Схема установки приведена на (рис. 1). Шары А подвешены на двух металлических нитях каждый, что предохраняет их от вращения вокруг вертикальных осей. Шары удерживаются в отклоненном положении двумя электромагнитами М, цепи которых соединены последовательно. При размыкании ключом К1 этой цепи шары освобождаются и ударяются друг о друга. Расстояния, проходимые шарами, измеряются по шкале Е. Двойной перекидной ключ К2 служит для зарядки конденсатора С (0,5 мкф) от батареи В (2,6 в) и для разрыва цепи ударяющихся шаров. В верхнем (на схеме) положении ножей ключа конденсатор заряжается, в нижнем при соударении шаров он разряжается. Разомкнутое состояние ключа позволяет временно сохранить полный заряд конденсатора или его часть после соударения шаров.
Ключ последовательного действия К3 при его нажатии сначала размыкает цепь гальванометра G (проводником l эта цепь замкнута), а позже замыкает гальванометр на заряженный конденсатор. Рамка гальванометра приходит в движение, “зайчик” от осветителя дает смещение по шкале прибора. Прекращение нажатия на ключ К3 размыкает цепь “конденсатор-гальванометр” и замыкает цепь гальванометра на малое сопротивление проводника l, что ведет к успокоению его колебаний.
Если ошибки, связанные с определением n0 и n, положить равными, т.е.
Dn = Dn0 , 
 то относительная ошибка, связанная с определением логарифма, будет равна
то относительная ошибка, связанная с определением логарифма, будет равна
 . (12)
. (12)
При заданных n0 и Dn эта ошибка возрастает при  n
n 
и при 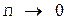 . Наиболее оптимальные значения n, соответствующие минимуму выражения (12), составляют 20-30 % от n0. В соответствии с этим при С = 0,5 мкф и имеющихся временах соударения величина R должна быть ориентировочно 200-300 ом. При таком сопротивлении цепи разрядки можно не учитывать сопротивление контакта шаров, которое в процессе соударения не остается постоянным. В работе применяется гальванометр типа ГЗБ-47.
. Наиболее оптимальные значения n, соответствующие минимуму выражения (12), составляют 20-30 % от n0. В соответствии с этим при С = 0,5 мкф и имеющихся временах соударения величина R должна быть ориентировочно 200-300 ом. При таком сопротивлении цепи разрядки можно не учитывать сопротивление контакта шаров, которое в процессе соударения не остается постоянным. В работе применяется гальванометр типа ГЗБ-47.
Измерения. 1. Для измерения коэффициента восстановления достаточно собрать цепь электромагнитов и убедиться в правильности подвеса шаров. Необходима их хорошая центрировка для получения центрального удара.
Убедившись, что начальные отклонения обоих шаров одинаковы, размыкают ключ К1 и, отсчитав 10-16 соударений, измеряют величину Sn (отклонение шара после последнего удара). Это проделывают 3-5 раз, измеряя величину Sn для каждого шара. Вычисляют среднее арифметическое значение этой величины. Затем измеряют амплитуду S’n n-го неполного колебания одного шара (т.е. без соударений), причем n равно числу соударений при определении Sn. Величина коэффициента восстановления определяется по формуле (8).
2. Для определения времени соударения шаров необходимо собрать схему полностью. После ее сборки включают освещение гальванометра и отмечают положение “ зайчика” на шкале прибора (нулевое положение). Затем определяют величину наибольшего смещения “зайчика” (от нулевого положения), которое соответствует прохождению через гальванометр всего заряда Q0.
Для этого замыкания ключ К2 на батарею, затем размыкают его и замыкают ключ К3, удерживая его в этом положении до тех пор, пока не начнется обратное движение “зайчика”.
По шкале прибора отсчитывают величину n0, при этом пользуются средним арифметическим из трех отдельных смещений “зайчика”. После этого вновь замыкают ключ К2 на батарею и включают цепь электромагнитов; шары должны находиться в отклоненном положении (притянуты к электромагнитам).
Ножи ключа К2 переводят в нижнее положение (замыкают цепь шаров);
ключом К1 размыкают цепь электромагнита. После первого соударения шаров ключ К2 ставят в положение, размыкающее обе цепи - цепь батареи и цепь шаров (вертикально). Ключом К3 замыкают цепь гальванометра и по шкале прибора отсчитывают величину n. Все эти операции проделываюи три раза. При замыкании ключа К3 его необходимо удерживать в этом положении до тех пор, пока не начнется обратное движение “зайчика”. Время соударения определяется по формуле (11).
Нельзя забывать перед нажатием ключа К3 размыкать ключом К2 цепи батареи и шаров (ставить ножи вертикально).
Упрощенная схема установки и расчетные формулы к определению времени соударения шаров
 Принципиальная электрическая схема экспериментальной установки.
Принципиальная электрическая схема экспериментальной установки.
1,2 – шары – контакты, Тр – понижающий трансформатор, С - конденсатор, R – резистор, V – вольтметр, VD – диодный мост, К – ключ.
Расчетные формулы:
 (1)
(1)
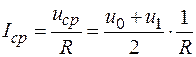 (2)
(2)
 (3)
(3)
 (4)
(4)
 (5)
(5)
Порядок выполнения работы:
Собрать схему. Для этого включить удлинитель в сеть 220 В, убедиться, что он исправен и выключить его. Затем к удлинителю подсоединить блок, содержащий конденсатор. При этом блок должен быть выключен. Развести шары на установке, используя магнит. После этого подключить контакты шаров к блоку с конденсатором. Включить этот блок, затем включить удлинитель и с помощью вольтметра контролировать процесс зарядки конденсатора. После того, как напряжение на конденсаторе перестает быстро расти, можно производить соударение шаров.
Внимание!
При зарядке конденсатора следить за тем, чтобы шары-контакты были разомкнуты. это их нормальное состояние. Для этого один из шаров должен обязательно находиться на магните. Перед соударением шар, висящий в положении равновесия, отводится рукой, а другой шар, по которому будет производиться удар, снимается с магнита и переводится в положение равновесия. Первый шар отпускают, он ударяет второй и отбрасывает его на магнит.
Соударение шаров следует производить тогда, когда напряжение на конденсаторе, регистрируемое вольтметром, больше не растет. Для этого требуется порядка 3-х минут с момента включения напряжения сети.
После того, как произведен первый удар, следует отключить установку от сети и дать заряду стечь с конденсатора, при этом напряжение на нем станет нулевым. Для этого нужно порядка 10-ти минут. После этого следует снова зарядить конденсатор и произвести второе соударение.
1.Замерить напряжение U0 на конденсаторе при разомкнутых шарах спустя 3 мин после включения в сеть.
2. Замерить напряжение U1 сразу после соударения шаров.
3. Произвести измерения несколько раз и взять средние значения U0 и U1. Данные занести в таблицу.
В схеме принять R = 1 кОм, С = 2 мкФ.
| № | U0 | U1 | № | U0 | U1 |
Uср = τ =
Контрольные вопросы:
1. Какой удар называется абсолютно упругим?, абсолютно неупругим?, частично упругим?
2. Опишите, что происходит с деформациями тел при этих ударах.
3. Опишите, что происходит с энергией тел при этих ударах.
4. Опишите, что происходит с импульсом тел при этих ударах.
5. Какой удар называется центральным?
6. Какой удар называется косым?
7. Где применяется и как используется явление удара?






