Векторная алгебра
Вектором  называется направленный отрезок в пространстве (на плоскости). Вектор имеет две характеристики: длину, называемую также модулем и обозначаемую
называется направленный отрезок в пространстве (на плоскости). Вектор имеет две характеристики: длину, называемую также модулем и обозначаемую  и направление. Принято также вектор обозначать двумя буквами, первая из которых указывает начало вектора, вторая – конец:
и направление. Принято также вектор обозначать двумя буквами, первая из которых указывает начало вектора, вторая – конец:  .
.
Два вектора считаются равными, если они: 1) равны по длине, 2) лежат на параллельных прямых, 3) сонаправлены. Вектор, имеющий нулевую длину (то есть у которого совпадают начало и конец), называется нуль-вектором или нулевым вектором и обозначается 0, нуль-вектор считается параллельным любому вектору. Вектор, модуль которого равен единице, называется единичным вектором или ортом.
Суммой векторов  и
и  называется вектор
называется вектор  , определяемый по правилу: если путём параллельного переноса совместить начало вектора
, определяемый по правилу: если путём параллельного переноса совместить начало вектора  с концом вектора
с концом вектора  , то начало вектора
, то начало вектора  совпадает с началом
совпадает с началом  , а конец
, а конец  – с концом
– с концом  ; при этом пишут
; при этом пишут  . Векторы можно складывать и по «правилу параллелограмма».
. Векторы можно складывать и по «правилу параллелограмма».
Произведением вектора  на действительное число
на действительное число  называется вектор, обозначаемый
называется вектор, обозначаемый  и удовлетворяющий следующим требованиям: 1)
и удовлетворяющий следующим требованиям: 1)  ; 2)
; 2)  и
и  параллельны; 3)
параллельны; 3)  и
и  сонаправлены при
сонаправлены при  и направлены в противоположные стороны при
и направлены в противоположные стороны при  .
.
Эти две операции обладают привычными для нас свойствами:  ,
,  ,
,  и т.д.
и т.д.
Единичный вектор, параллельный  и сонаправленный с ним, называется ортом вектора
и сонаправленный с ним, называется ортом вектора  и обозначается
и обозначается  ;
;  . Векторы
. Векторы  называются коллинеарными, если они параллельны. Тройка векторов
называются коллинеарными, если они параллельны. Тройка векторов  называется компланарной, если путём параллельного переноса все три вектора удаётся поместить в одну плоскость.
называется компланарной, если путём параллельного переноса все три вектора удаётся поместить в одну плоскость.
Система векторов  называется линейно-зависимой, если существуют числа
называется линейно-зависимой, если существуют числа  , не все равные нулю и такие, что
, не все равные нулю и такие, что  . Если же равенство
. Если же равенство  возможно лишь при
возможно лишь при  , то система векторов
, то система векторов 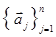 называется линейно независимой.
называется линейно независимой.
Теорема 1. а) Векторы  коллинеарны в том и только в том случае, если они линейно-зависимы; б) векторы
коллинеарны в том и только в том случае, если они линейно-зависимы; б) векторы  компланарны в том и только в том случае, если они линейно-зависимы.
компланарны в том и только в том случае, если они линейно-зависимы.
Упорядоченная тройка  (двойка
(двойка  ) некомпланарных (неколлинеарных) векторов пространства (плоскости) называется базисом во множестве всех векторов пространства (плоскости). Любой вектор
) некомпланарных (неколлинеарных) векторов пространства (плоскости) называется базисом во множестве всех векторов пространства (плоскости). Любой вектор  в пространстве может быть представлен в виде линейной комбинации векторов базиса
в пространстве может быть представлен в виде линейной комбинации векторов базиса  :
:
 ,
,
более того, такое представление единственно; числа  называются координатами вектора
называются координатами вектора  в базисе
в базисе  .
.
При сложении векторов складываются их соответствующие координаты; при умножении вектора на число каждая координата вектора умножается на это число. Векторы  и
и  коллинеарны в том и только в том случае, если координаты этих векторов (в произвольном базисе) пропорциональны. Если векторы
коллинеарны в том и только в том случае, если координаты этих векторов (в произвольном базисе) пропорциональны. Если векторы  единичные и взаимно перпендикулярны, то они образуют базис, который называется ортонормированным.
единичные и взаимно перпендикулярны, то они образуют базис, который называется ортонормированным.
Упорядоченная тройка некомпланарных векторов  образует правую (левую) тройку, если после совмещения их начал путём параллельного переноса, кратчайший поворот от первого вектора
образует правую (левую) тройку, если после совмещения их начал путём параллельного переноса, кратчайший поворот от первого вектора  ко второму вектору
ко второму вектору  виден из конца третьего вектора
виден из конца третьего вектора  , совершающимся против (по) часовой стрелки. Для ортонормированного базиса
, совершающимся против (по) часовой стрелки. Для ортонормированного базиса  , образующего правую тройку, приняты обозначения
, образующего правую тройку, приняты обозначения  .
.
Проекцией вектора  на вектор
на вектор  (или на ось, параллельную и сонаправленную
(или на ось, параллельную и сонаправленную  ) называют число
) называют число  , где j – угол между векторами
, где j – угол между векторами  и
и  . В ортонормированном базисе координаты X, Y, Z вектора
. В ортонормированном базисе координаты X, Y, Z вектора  совпадают с его проекциями на базисные орты
совпадают с его проекциями на базисные орты  :
:  при этом
при этом  . Обозначим через
. Обозначим через  углы между вектором
углы между вектором  и векторами
и векторами  соответственно. Числа
соответственно. Числа  называются направляющими косинусами вектора
называются направляющими косинусами вектора  . Имеют место формулы:
. Имеют место формулы:
 ,
,  ,
, 
Часто краткости ради вместо  пишут
пишут  . Аналогичные определения приняты на множестве векторов плоскости.
. Аналогичные определения приняты на множестве векторов плоскости.
Теорема 2. Тройка векторов  ,
,  ,
,  образует базис в том и только в том случае, если
образует базис в том и только в том случае, если
 .
.
Прямоугольная система координат в пространстве задаётся точкой О – началом координат – и ортонормированным базисом  . Оси Оx, Оy, Оz, проведённые через точку О параллельно векторам
. Оси Оx, Оy, Оz, проведённые через точку О параллельно векторам  , называются координатными осями.
, называются координатными осями.
Каждой точке M пространства ставится в соответствие вектор  , называемый радиус-вектором точки M; это соответствие является взаимно-однозначным. Координатами x, y, z точки M называются координаты её радиус-вектора
, называемый радиус-вектором точки M; это соответствие является взаимно-однозначным. Координатами x, y, z точки M называются координаты её радиус-вектора  Координаты вектора
Координаты вектора  выражаются через координаты начала
выражаются через координаты начала  и конца
и конца  вектора по формулам:
вектора по формулам:
 ,
,  ,
,  . Расстояние между точками
. Расстояние между точками  и
и  выражается формулой
выражается формулой
 .
.
Скалярным произведением  векторов
векторов  и
и  называется произведение модулей этих векторов на косинус угла между
называется произведение модулей этих векторов на косинус угла между  и
и  :
:  . (Наряду с обозначением
. (Наряду с обозначением  принято и другое:
принято и другое:  ).
).
Теорема 3. а) Пусть 
 ,
,  . Тогда
. Тогда  в том и только в том случае, если
в том и только в том случае, если  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  , причём
, причём  в том и только в том случае, если
в том и только в том случае, если  .
.
Из определения скалярного произведения следует:  ,
,  .
.
Теорема 4. Если  ,
,  , то
, то  .
.
Отсюда следует формула косинуса угла между векторами  и
и  :
:
 .
.
 в том и только в том случае, если
в том и только в том случае, если  .
.
Векторным произведением  упорядоченной пары неколлинеарных векторов
упорядоченной пары неколлинеарных векторов  и
и  называется вектор
называется вектор  , удовлетворяющий следующим трём требованиям: 1)
, удовлетворяющий следующим трём требованиям: 1)  , где j – угол между векторами
, где j – угол между векторами  и
и  ; 2)
; 2)  перпендикулярен каждому из векторов
перпендикулярен каждому из векторов  и
и  ; 3)
; 3)  ,
,  ,
,  образуют правую тройку. Векторное произведение принято также обозначать
образуют правую тройку. Векторное произведение принято также обозначать  .
.
Теорема 5. a)  равен площади параллелограмма, построенного на векторах
равен площади параллелограмма, построенного на векторах  и
и  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
Теорема 6. Если  ,
,  , то
, то
 .
.
Смешанным произведением векторов  ,
,  ,
,  называется скалярное произведение векторов
называется скалярное произведение векторов  и
и  ; смешанное произведение векторов
; смешанное произведение векторов  ,
,  ,
,  обозначается
обозначается  .
.
Теорема 7. а)  ,
,  ,
,  компланарны в том и только в том случае, если
компланарны в том и только в том случае, если  ;
;
б) для некомпланарной тройки векторов  ,
,  ,
, 
 в том и только в том случае, если
в том и только в том случае, если  ,
,  ,
,  образуют правую тройку, и
образуют правую тройку, и  в том и только в том случае, если
в том и только в том случае, если  ,
,  ,
,  образуют левую тройку; в)
образуют левую тройку; в)  равен объёму параллелепипеда, построенного на векторах
равен объёму параллелепипеда, построенного на векторах  ,
,  ,
,  ;
;
г)  .
.
Теорема 8. Если  ,
,  ,
,  , то
, то
 .
.
Задания для самостоятельного решения
1. Векторы  и
и  образуют угол
образуют угол 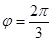 , также
, также  ,
,  .
.
Найти: 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ; 7)
; 7)  .
.
Ответ. 1) –6; 2) 9; 3) 16; 4) 13; 5) –61; 6) 37; 7) 73.
2. Найти координаты вектора  , если известно, что он перпендикулярен векторам
, если известно, что он перпендикулярен векторам 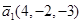 и
и  , образует с ортом
, образует с ортом  тупой угол и
тупой угол и  .
.
Ответ.  (-6,-24,8).
(-6,-24,8).
3. Найти координаты вектора  , если он перпендикулярен векторам
, если он перпендикулярен векторам  и
и  , а также удовлетворяет условию:
, а также удовлетворяет условию:  .
.
Ответ.  (7,5,1)
(7,5,1)
4. Даны A (4,2,5), B (0,7,2), C (0,2,7). Коллинеарны ли вектора  и
и  , если
, если  ,
,  ?
?
Ответ. Нет.
5. Компланарны ли данные векторы:
а) 
б) 
Ответ. а) компланарны; б) не компланарны.
6. При каком  векторы
векторы  будут компланарны, если:
будут компланарны, если:
а) 
б) 
Ответ. а) –3; б) любое.
7. Даны точки A (–3;2;–1), B (1;–1;4), C (2;0;1), D (1;–3;5).
Найдите: а) длину отрезка AB; б) косинус угла B в треугольнике ABC;
в)  ; г)
; г)  и направляющие косинусы вектора
и направляющие косинусы вектора  ;
;
д) площадь треугольника ABC;
е) высоту h треугольника ABC, опущенную из вершины C на сторону AB;
ж) объём пирамиды ABCD.
Ответ. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ,
,  ,
, 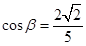 ,
,  ;
;
д)  ; е)
; е)  ; ж)
; ж)  .
.
8. Дано:  Найти:
Найти: 
Ответ. а) (-3,5,7); б) (-6,10,14); с) (-12,20,28).
9. Даны векторы:  ,
,  . При каком значении m эти векторы перпендикулярны?
. При каком значении m эти векторы перпендикулярны?
Ответ. m = 4.






