Материальная точка движется вдоль оси Х под действием упругой силы  и возмущающей силы
и возмущающей силы 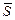 .Проекции этих сил на ось Х равны:
.Проекции этих сил на ось Х равны: 
Масса точки  ,амплитуда возмущающей силы
,амплитуда возмущающей силы  ,круговая частота этой силы
,круговая частота этой силы 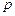 ,а также начальные условия заданы в таблице.
,а также начальные условия заданы в таблице.
Номер строки таблицы соответствует варианту задания.

1.Подобрать жесткость пружины из условия, чтобы коэффициент динамичности равнялся двум  для
для 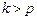 ,где
,где  – частота свободных колебаний.
– частота свободных колебаний.
2.Построить график зависимости амплитуды вынужденных колебаний от расстройки 
 по точкам, найденным для значений 0; 0,25; 0,5; 0,75; 0,9; 1; 1,1; 1,5; 2.
по точкам, найденным для значений 0; 0,25; 0,5; 0,75; 0,9; 1; 1,1; 1,5; 2.
3.Найти закон движения точки при заданных в таблице начальных условиях и найденном ранее значении коэффициента жесткости пружины.
ПРИМЕР. Груз массы m прикреплён к пружине, как показано на рисунке. На груз действует возмущающая сила  .
.
Найти жесткость пружины из условия, чтобы коэффициент динамичности в доризонансной зоне равнялся 
Построить график зависимости амплитуды вынужденных колебаний от расстройки.
Найти закон движения точки при следующих условиях:
 кг,
кг,  ,
,  ,
,  м,
м, 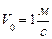 .
.
Груз считать материальной точкой
РЕШЕНИЕ
1.Найдем жесткость пружины. При отсутствии сил сопротивления коэффициент динамичности 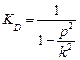 ,
,
Где  – частота свободных колебаний.
– частота свободных колебаний.
Пологая, что  и учитывая, что частота возмущения
и учитывая, что частота возмущения  ,найдём
,найдём 
С другой стороны, частота свободных колебаний
 ,
,
что позволяет найти коэффициент жесткости пружины

2.Амплитуду вынужденных колебаний рассчитываем по формуле

Где  –деформация пружины в случае статического действия силы Н,
–деформация пружины в случае статического действия силы Н,  .
.
3.Находим закон движения точки.
Дифференциальное уравнение вынужденных колебаний (см., например, Тарг С.М. Краткий курс теоретической механики.– М.:Высш. Шк.,1995)
 .
.
здесь  .
.
Общее решение уравнения равняется сумме общего решния однородного уравнения
 ,
,
которое обозначим Х1,и частного решения неоднородного уравнения Х2:
 .
.
Однородное уравнение имеет общее решение:
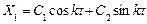 ,
,
Где  и
и  –постоянные интегрирования.
–постоянные интегрирования.
Частное решение неоднородного уравнения
 .
.
Таким образом,
 .
.
Подсчитаем значение А для следующих расстройки:
 : 0; 0,25; 0,5; 0,75; 0,9; 1; 1,1;1, 25; 1, 5;2.
: 0; 0,25; 0,5; 0,75; 0,9; 1; 1,1;1, 25; 1, 5;2.
При 
 .
.
При 
 .
.
По аналогичным формулам найдем амплитуду вынужденных колебаний при других значениях  и результаты вычислений занесем в таблицу
и результаты вычислений занесем в таблицу
| Z | 0 | 0,25 | 0,5 | 0,75 | 0,9 | 1 | 1,1 | 1,25 | 1,5 | 2 |
| 104м | 2,78 | 2,79 | 3,71 | 6,35 | 14,43 | ¥ | 13,24 | 4,94 | 2,22 | 0,93 |
По этим данным строем график А=А(z),который называется амплитудно-частотной характеристикой.

Найдём постоянные интегрирования  и
и  из начальных условий.
из начальных условий.
При  ,
,  м. отсюда находим
м. отсюда находим  м
м
Чтобы определить  найдем выражение скорости точки по формуле
найдем выражение скорости точки по формуле 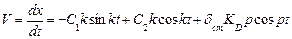 .
.
Согласно условию задачи при 
 м/с.
м/с.

Найдём  :
:
 м.
м.
Итак, движение точки определяется выражением

Ответ:
 ,
, 
Варианты задачи 7.
| Номер варианта | Масса (кг) | Амплитуда силы Н(H) | Круговая частота p(c-1) | X0(м) | 
|
| 0,4 | 0,03 | ||||
| 1,2 | |||||
| 0,8 | 0,04 | ||||
| 0,02 | |||||
| 0,8 | |||||
| 0,6 | 0,05 | ||||
| 0,01 | |||||
| 2,4 | |||||
| 0,03 | |||||
| 0,6 | |||||
| 0,9 | 0,1 | ||||
| 1,4 | 2,2 | ||||
| 0,008 | |||||
| 0,7 | |||||
| 3,6 | 0,02 | ||||
| 0,8 | 2,8 | ||||
| 10,6 | 0,018 | ||||
| 7,6 | |||||
| 0,9 | 0,1 | ||||
| Номер варианта | Масса (кг) | Амплитуда силы Н(H) | Круговая частота p(c-1) | X0(м) | 
|
| 1,2 | 1,5 | ||||
| 2,8 | 0,08 | ||||
| 5,6 | |||||
| 6,8 | 0,012 | ||||
| 0,65 | 1,6 | ||||
| 4,7 | 0,015 | ||||
| 1,5 | |||||
| 0,06 | |||||
| 2,8 | 2,4 |
ЗАДАЧА № 8
ПРИНЦИП ДАЛАМБЕРА
Вертикальный вал  вращается с постоянной угловой скоростью
вращается с постоянной угловой скоростью 

 с-1, закреплён подпятником и цилиндрическим подшипником.
с-1, закреплён подпятником и цилиндрическим подшипником.
К валу жестко прикреплен невесомый стержень 1 длинной  м,
м,
точечной массой  кг на конце и однородный стержень 2 длинной
кг на конце и однородный стержень 2 длинной  м, имеющий массу
м, имеющий массу  кг; оба стержня лежат в одной плоскости.
кг; оба стержня лежат в одной плоскости.
Пренебрегая весом тела, определить реакции подпятника и подшипника. При окончательных расчётах принять  м.
м.
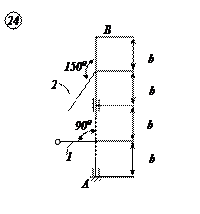
ПРИМЕР. С невесомым валом  , вращающимся с постоянной угловой скоростью
, вращающимся с постоянной угловой скоростью  , жестко скреплен стержень ОД длинной
, жестко скреплен стержень ОД длинной 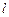 и массой
и массой  ,имеющий на конце груз массой
,имеющий на конце груз массой 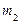 .
.
Определить реакции подпятника А и подшипника В.




РЕШЕНИЕ. Рассмотрим систему состоящую из вала АВ и стержня ОД, и покажем на рисунке внешние силы, действующие на систему; силы тяжести  и
и  , составляющие
, составляющие  и
и  реакции подпятника и реакция
реакции подпятника и реакция  подпятника.
подпятника.
Согласно принципу Даламбера, присоединим к этим силам силы инерции элементов (точек) стержня и груза. Так как вал вращается равномерно, то все его элементы имеют только нормальные ускорения, направленные к оси вращения.
 ,
,
где 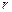 – расстояние элемента стержня от оси.
– расстояние элемента стержня от оси.
Тогда сила инерции элемента стержня  ,где
,где  – масса элемента. Эта сила представляет собой распределённую нагрузку, пропорциональную расстоянию
– масса элемента. Эта сила представляет собой распределённую нагрузку, пропорциональную расстоянию 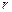 (см. рисунок).и направлена в сторону противоположную
(см. рисунок).и направлена в сторону противоположную  . Распределённую нагрузку заменяем равнодействующей
. Распределённую нагрузку заменяем равнодействующей  , причем её величина
, причем её величина
 ,
,
где  – масса стержня;
– масса стержня;
 – ускорение его масс С.
– ускорение его масс С.
Приложена эта сила в точке  , где
, где 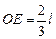 . Направление силы показано на рисунке.
. Направление силы показано на рисунке.
Сила инерции груза  .
.
Так как все действующие силы и силы инерции лежат в плоскости  ,то и реакции подпятника
,то и реакции подпятника  и подшипника
и подшипника  тоже лежат в этой плоскости, что было учтено в начале решения
тоже лежат в этой плоскости, что было учтено в начале решения
По принципу Даламбера приложенные внешние силы и силы инерции образуют уравновешенную систему сил. Составим для этой системы уравнения равновесия:
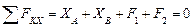 ;
;
 ;
;

Подставляя сюда числовые значения сил веса
 ,
,
 .
.
и определённые ранее силы инерции  и
и  , найдем искомые реакции
, найдем искомые реакции
 ,
, 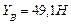 ,
,  .
.
Знаки указывают что силы  и
и  направлены противоположно показанным на рисунке.
направлены противоположно показанным на рисунке.
Ответ:  ,
,  ,
, 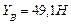 .
.

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Практикум
для студентов факультета заочного обучения
ЗАЙЦЕВ Александр Семенович
МИЗОНОВ Вадим Евгеньевич
ШАПИН Вадим Иванович
Редактор
Компьютерная верстка Г.Н. Чернова
Лицензия ИД № 05285 от 4 июля 2001 года
Подписано в печать Формат 60х84 1\1б. Печать плоская.
Усл. печ. л. Тираж 400 экз.
ГОУВПО «Ивановский государственный энергетический университет имени В.И. Ленина»
I 53003, г. Иваново, ул. Рабфаковская, 5
Отпечатано в РИО ИГЭУ.
|






