ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Практикум
Для студентов факультета заочного обучения
Иваново 2009
Составители: А.С. ЗАЙЦЕВ
В.Е. МИЗОНОВ
В.И. ШАПИН
Редактор А.Б. КОЛОБОВ
Контрольные задачи практикума предназначены для студентов всех специальностей факультета заочного обучения ИГЭУ и могут быть использованы в качестве учебного материала студентами, обучающимися по дневной форме.
Утверждены цикловой методической комиссией электромеханического факультета
Рецензент
кафедра теоретической и прикладной механики ГОУВПО «Ивановский государственный энергетический университет имени В.И. Ленина»
 |
СОДЕРЖАНИЕ
| Указания к выполнению контрольной работы......... | ||
| Задача №1. Равновесие плоской системы параллельных сил.................................................................. | ||
| Задача №2. Равновесие плоской системы сил (Общий случай)….............................................................. | ||
| Задача №3. Кинематика точки…………..…………. | ||
| Задача №4. Плоское движение твердого тела……... | ||
| Задача №5. Сложное движение точки……………... | ||
| Задача №6. Динамика точки……………………….. | ||
| Задача №7. Колебания материальной точки………. | ||
| Задача № 8. Принцип Даламбера…………………... |
УКАЗАНИЯ К ВЫПОЛНЕНИЮ
КОНТРОЛЬНОЙ РАБОТЫ
Контрольная работа студента-заочника состоит из двух частей:
- контрольная работа №1, включающая в себя задачи 1–5 (статика и кинематика);
- контрольная работа №2, состоящая из задач 6–10 (динамика).
Число задач может быть уменьшено решением кафедры, при согласовании с деканатом факультета заочного обучения. В этом случае студенты информируются дополнительным указанием.
Прежде, чем приступить к решению задач, студент должен внимательно изучить следующие темы по учебнику (например, Тарг С.М. Краткий курс теоретической механики. –М,: Высш.шк., 1995).
Статика
- Основные типы связей и их реакции.
- Момент силы, пара сил и их свойства.
- Условия и уравнения равновесия для различных систем сил.
Кинематика
- Кинематика точки.
- Простейшие виды движения твердого тела (поступательное и вращение вокруг твердой оси).
- Плоскопараллельное движение твердого тела.
- Сложное движение точки.
Динамика
- Динамика точки.
- Прямолинейные колебания точки.
- Общие теоремы движения.
- Принцип Даламбера.
Свой вариант студент определяет по двум последним цифрам зачетной книжки (т.е. если, например, номер зачетной книжки заканчивается цифрами 12, то Ваш вариант 12, если 05 – вариант 5 и т.д.).
Если номер зачетной книжки заканчивается числом большим, чем число вариантов задания, то номер Вашего варианта определяется разностью двух последних цифр зачетной книжки и числом вариантов. Например: две последние цифры зачетной книжки – 31. Задание имеет 28 вариантов. Ваш вариант – 3 (31–28=3). Варианты задач указаны на рисунках в кружках.
Многие величины, определяемые в ходе решения, являются векторными, поэтому следует не только найти их модуль, но и указать на рисунке направления этих векторов (а также их компонентов).
Для удобства на каждый тип задач рассмотрен пример. С целью экономии места рисунки заданий примеров часто расположены в тексте решения задачи.
Решения задач следует сопровождать краткими комментариями, рисунки выполняться с помощью чертежных инструментов. Расчеты ведутся с точностью до третьей значащей цифры. Почерк должен быть разборчивым. Если записи допускают двойную трактовку, то они считаются ошибочными.
В тетради должны быть предусмотрены поля для замечаний проверяющего.
Задачи, выполненные с отклонением от вышеизложенных указаний, не проверяются и считаются незачтёнными.
ЗАДАЧА №1
РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ СИЛ
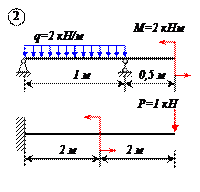
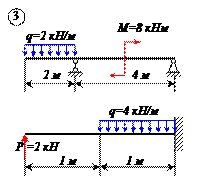
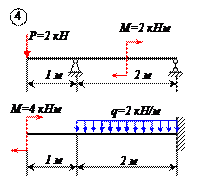
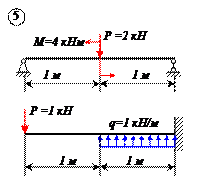
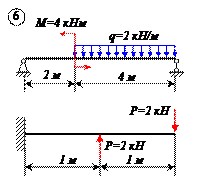
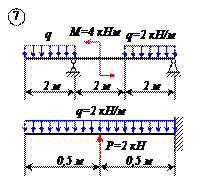
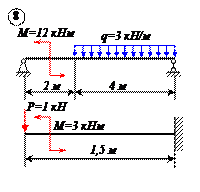
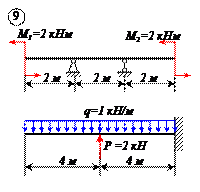
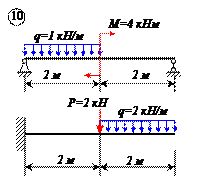
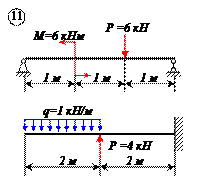
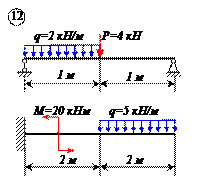
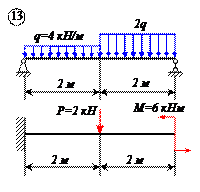
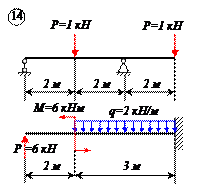
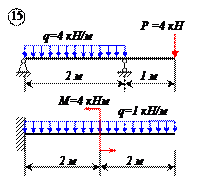
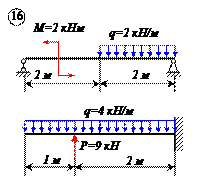
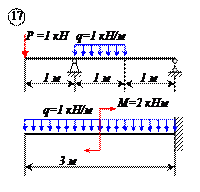
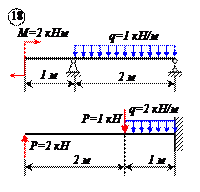
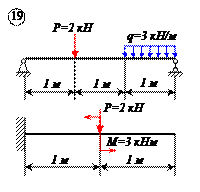
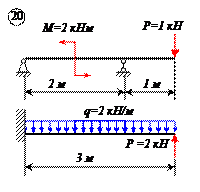
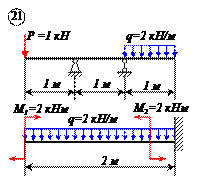
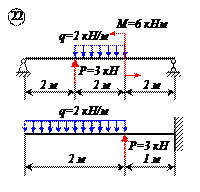
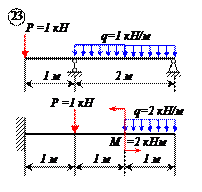
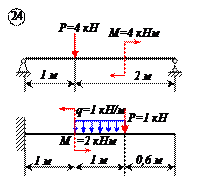
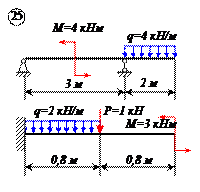
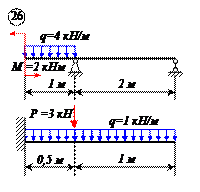
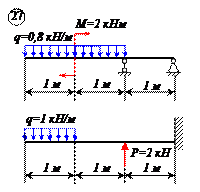
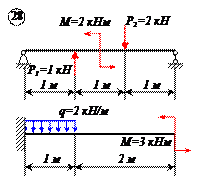
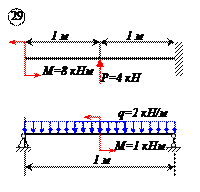
Определить реакции связей для балок, изображенных на рисунке.
Примечание: каждый вариант включает в себя две схемы балок.
ПРИМЕР 1.
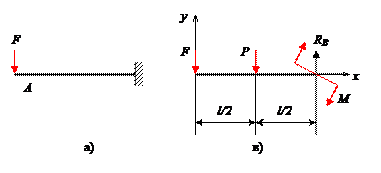
Балка АВ весом Р и длиной l заделана правым концом в стену. В точке А на балку действует вертикальная сила F. Определить реакцию стены.
РЕШЕНИЕ
Отбросим связь–стену и заменим её действие реакцией (рис.в). Горизонтальная составляющая реакции стены равна в данном случае нулю, так как все активные силы, действующие на балку, вертикальны. Реакция стены состоит из вертикальной составляющей RB и пары сил с моментом М.
Выбираем оси координат: ось х направлена по балке АВ, ось у – по вертикали из точки А.
Запишем уравнение равновесия. Для плоской системы параллельных сил имеем два уравнения равновесия. Возьмём следующие уравнения – сумму проекций сил на ось у и сумму моментов всех сил относительно точки В:
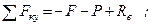
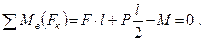
Из первого уравнения находим силу 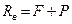 .
.
Из второго уравнения определяем момент пары сил 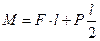 .
.
ПРИМЕР 2.
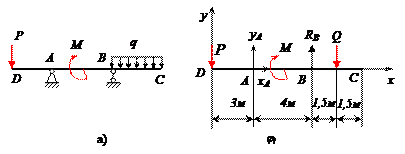
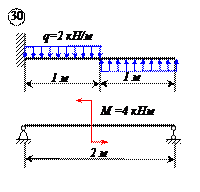
Двухконсольная горизонтальная балка шарнирно закреплена в точке А и опирается на каток в точке В. На балку действует вертикальная сила Р =20 Н, приложенная в точке D, равномерно распределённая вертикальная нагрузка на участке ВС интенсивностью q =25 Н/м и пара сил, момент которой равен М =40 Нм. Длины участков: AD =3 м, АВ =4 м, ВС =3 м. Определить реакции опор, пренебрегая весом балки.
РЕШЕНИЕ
Отбросим мысленно связи и заменим их реакциями. Реакция в точке В RВ направлена по вертикали. Реакция шарнира А может иметь любое направление в плоскости. Поэтому заменяем её двумя составляющими ХА и УА . Распределённую нагрузку заменим силой 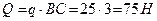 . Сила Q приложена в середине участка ВС.
. Сила Q приложена в середине участка ВС.
Проведем оси координат (рис.в) и запишем уравнения равновесия. Так как проекция силы ХА является единственной силой, проецирующейся на ось Х, то, следовательно, ХА=0.
Заметим, что сумма проекций сил, образующих пару, на любую ось равна нулю, так как силы, образующие пару сил, равны Модулу, параллельны и направлены в противоположные стороны.
Итак, учитывая, что ХА=0, имеем систему параллельных сил. Записываем для такой системы два уравнения равновесия, при этом следует стремиться к таким уравнениям равновесия, в каждое из которых входила бы только одна неизвестная величина. Для двухопорных балок это сумма моментов относительно опор.
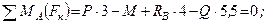
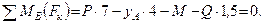
Находим реакции:
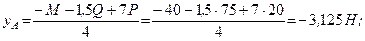
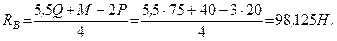
Для проверки решения можно составить «лишнее» уравнение равновесия.
Варианты задачи 1.
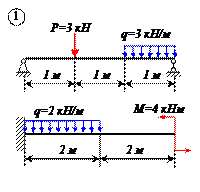
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
ЗАДАЧА №2
РАВНОВЕСИЕ ПЛОСКОЙ
СИСТЕМЫ СИЛ
(общий случай)
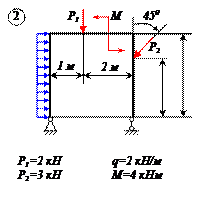
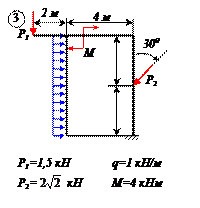
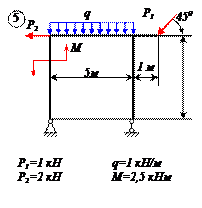
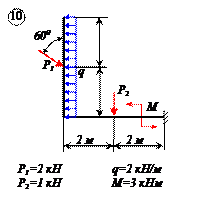
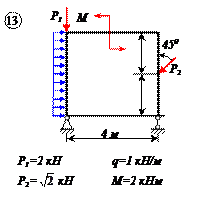
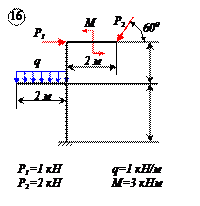
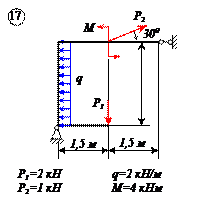
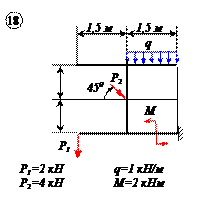
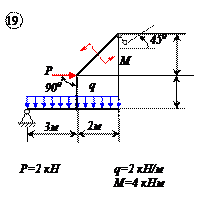
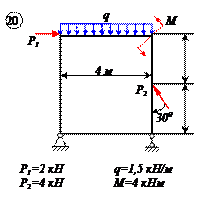
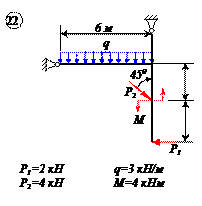
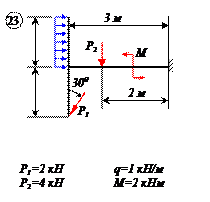
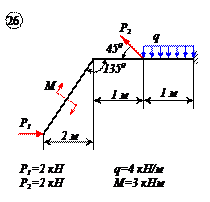
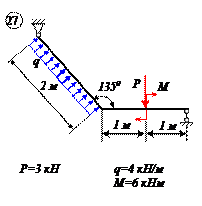
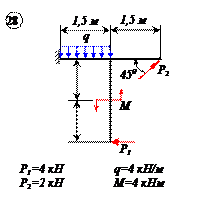
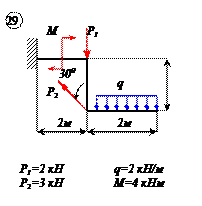
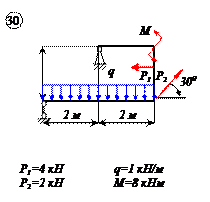
Найти реакции связей рамы, схема которой представлена на рисунке.
ПРИМЕР
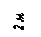  
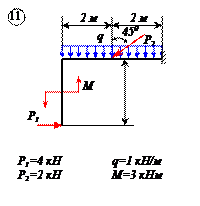
| Дано: F = 10 кН, P = 5 кН, M = 8 кНм, q = 0,5 кН/м. Определить реакцию опоры А и реакцию стержня BD. |
РЕШЕНИЕ
На раму наложены следующие связи: шарнирно-неподвижная опора, стержень BD и нить. Отбросим связи, заменив их силами.
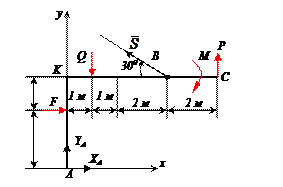
Так как направление реакции шарнирно-неподвижной опоры А неизвестно, то определим её составляющие  и
и 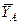 . Реакция стержня
. Реакция стержня  направлена вдоль этого стержня, реакция нити по модулю равна весу груза Р. Распределённую нагрузку интенсивностью q заменим сосредоточенной силой Q, равной
направлена вдоль этого стержня, реакция нити по модулю равна весу груза Р. Распределённую нагрузку интенсивностью q заменим сосредоточенной силой Q, равной 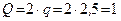 кН и приложенной в центре тяжести эпюры этой нагрузки. Проводим оси координат.
кН и приложенной в центре тяжести эпюры этой нагрузки. Проводим оси координат.
Для плоской системы сил, приложенных к раме, составим три уравнения равновесия:
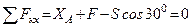 ; (1)
; (1)
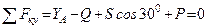 ; (2)
; (2)
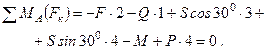 (3)
(3)
Момент от силы S найден с использованием теоремы Вариньона: момент равнодействующей равен сумме моментов составляющих.
Из уравнения (3) находим
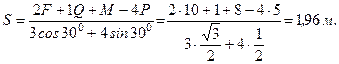
Из уравнения (1) –

Из уравнения (2) –
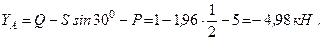
Ответ: 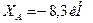 ,
, 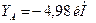 ,
, 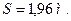
Знаки минус в значениях ХА и УА указывают на то, что принятые направления этих сил противоположны действительным.
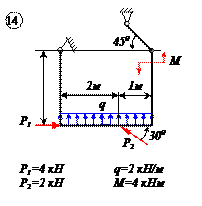
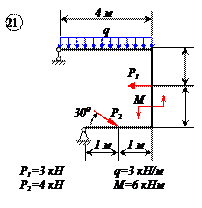
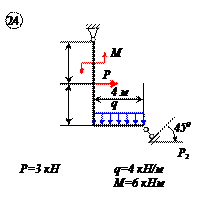
Варианты задачи 2.
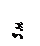 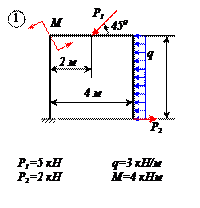
| 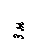 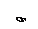 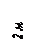 
|
|   
|
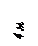 
| 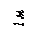  
|
| 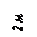 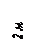 
|
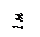 
| 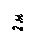 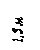 
|
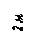 
| 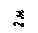 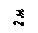 
|
|  
| ||
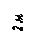 
|  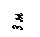 
| ||
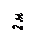 
|   
| ||
 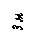 
| 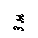 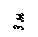 
| ||
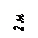 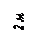 
|   
| ||
|  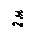 
| ||
| 
| ||
|   
| ||
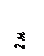 
| 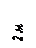 
| ||
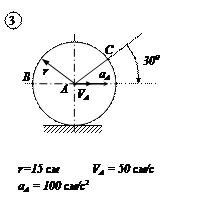
ЗАДАЧА №3
КИНЕМАТИКА ТОЧКИ
По заданным уравнениям движения точки М найти и изобразить на рисунке вид её траектории. Для момента времени 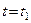 (с) указать положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории в соответствующей точке. Указать на рисунке векторы скорости и ускорения, а также все найденные в ходе решения задачи их компоненты.
(с) указать положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории в соответствующей точке. Указать на рисунке векторы скорости и ускорения, а также все найденные в ходе решения задачи их компоненты.
Варианты задачи 3.
| № варианта | Уравнения движения | 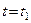 (с) (с)
| |
| Х=Х(t) м | Y=Y(t) м | ||
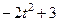
| 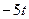
| 0,5 | |
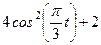
| 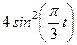
| ||
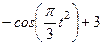
| 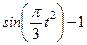
| ||
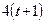
| 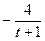
| ||
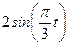
| 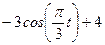
| ||
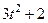
| 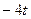
| 0,5 | |
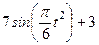
| 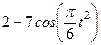
| ||
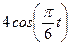
| 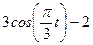
| ||
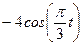
| 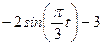
| ||
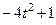
| 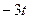
| 0,5 |
| № варианта | Уравнения движения | 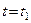 (с) (с)
| |
| Х=Х(t) м | Y=Y(t) м | ||
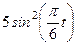
| 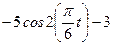
| ||
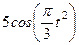
| 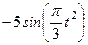
| ||
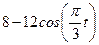
| 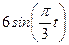
| ||
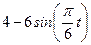
| 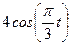
| ||
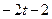
| 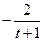
| ||
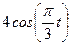
| 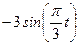
| ||
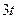
| 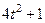
| 0,5 | |
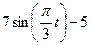
| 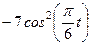
| ||
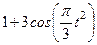
| 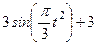
| ||
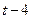
| 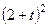
| ||
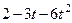
| 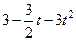
| ||
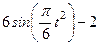
| 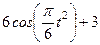
| ||
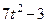
| 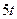
| 0,25 | |
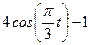
| 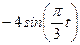
|
| № варианта | Уравнения движения | 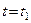 (с) (с)
| |
| Х=Х(t) м | Y=Y(t) м | ||
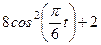
| 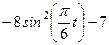
| ||
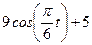
| 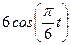
| ||
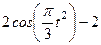
| 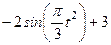
| ||
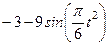
| 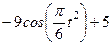
| ||
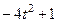
| 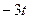
| ||
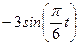
| 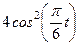
|
УКАЗАНИЯ. В некоторых вариантах при определении траектории следует учесть известные из тригонометрии формулы:
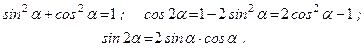
Касательное ускорение можно находить по формуле
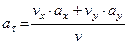 .
.
ПРИМЕР
Даны уравнения движения точки в плоскости ху:
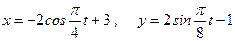 ,
,
где х, у – в метрах, t – в секундах.
Определить уравнение траектории точки для момента времени t1=1 с найти скорость и ускорение точки, а также её касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
РЕШЕНИЕ
1. Для определения уравнения траектории точки исключаем из уравнений движения t. Поскольку t входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу
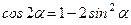 или
или 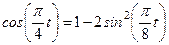 .
.
Из уравнений движения находим выражения соответствующих функций и подставляем их в предыдущее выражение:
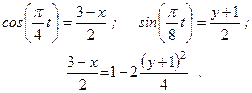
Окончательно находим
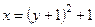 .
.
Строим график этой функции, представляющий собой в данном случае параболу.
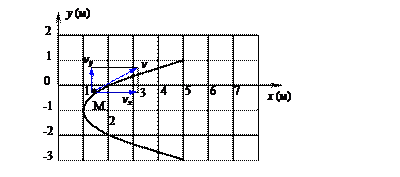
Определим положение точки на траектории:
 м;
м;
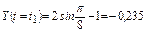 м.
м.
2. Скорость точки найдём по её проекциям на координатные оси:
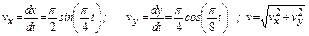 .
.
При t = 1 с
vx = 1,11 м/с, vу = 0,73 м/с, v = 1,33 м/с.
3. Аналогично найдём ускорение точки:
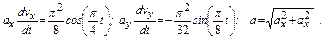
При t= 1 с
аx = 0,87 м/с2, ау = –0,12 м/с2, а = 0,88 м/с2.
4. Касательное ускорение найдём по формуле
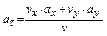 .
.
Подставляя ранее найденные числовые значения, получаем
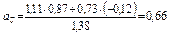 м/с2.
м/с2.
5. Нормальное ускорение
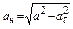 .
.
При t =1 с получаем ан = 0,58 м/с2.
Изобразим вектор ускорения точки и его составляющие, причём правильность решения контролируем как по составляющим 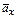 и
и  , так и по
, так и по 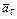 и
и 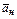 , т.е.
, т.е.
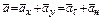 .
.
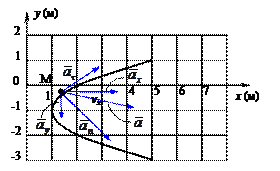
6. Радиус кривизны траектории 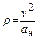 .
.
Подставляя численные значения, находим
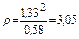 м.
м.
Ответ: v = 1,33 м/с, а = 0,88 м/с2, аt = 0,88 м/с2, ан = 0,58 м/с2,
r = 3,05 м.
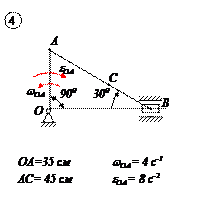
ЗАДАЧА №4
ПЛОСКОЕ ДВИЖЕНИЕ
ТВЕРДОГО ТЕЛА
Для заданного положения механизма найти:
1. Скорости точек В и С и угловую скорость тела, которому они принадлежат.
2. Ускорение этих точек и угловое ускорение указанного в пункте 1 тела.
Примечание: внимательно ознакомьтесь с указаниями кафедры. Возможно, пункт 2 этой задачи выполнять не следует.
ПРИМЕР
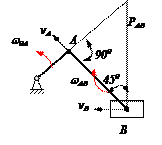
Для кривошипно-ползунного механизма найти скорость и ускорение точки В, а также угловую скорость и угловое ускорение шатуна АВ в момент, когда кривошип и шатун взаимно перпендикулярны и образуют с горизонтальной осью углы a = 45° и b = 45°.
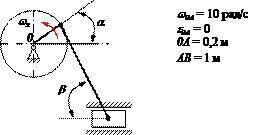
РЕШЕНИЕ
1. Определение скоростей точек.
Вычисляем скорость пальца А кривошипа 0А. 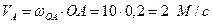 . Вектор
. Вектор 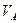 направлен по касательной к траектории, то есть перпендикулярно OA.
направлен по касательной к траектории, то есть перпендикулярно OA.
Скорость ползуна В направлена по горизонтали. Мгновенный центр скоростей РАВ шатуна АВ находится в точке пересечения перпендикуляров, проведённых их точек А и В к их скоростям.
Угловая скорость звена АВ 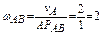 рад/с.
рад/с.
Скорость точки В  м/с.
м/с.
Здесь АРАВ= 1 м и ВРАВ= 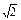 м находятся из прямоугольного равнобедренного треугольника АВРАВ .
м находятся из прямоугольного равнобедренного треугольника АВРАВ .
Скорость точки В можно найти также по теореме о проекциях скоростей двух точек:
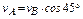 , отсюда
, отсюда 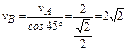 м/с.
м/с.
2. Определение ускорения точек.
Ускорение точки А складывается из нормального и касательного ускорений:
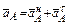 ;
; 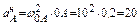 м/с.
м/с.
Касательное ускорение 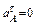 , поскольку
, поскольку 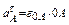 , а e 0 А по условию равняется нулю. Таким образом,
, а e 0 А по условию равняется нулю. Таким образом, 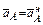 и вектор направлен от А к 0.
и вектор направлен от А к 0.
Согласно теореме об ускорениях точек плоской фигуры имеем
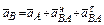 .
.
Нормальное ускорение В относительно A
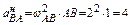 м/с2 и направлено от В к А.
м/с2 и направлено от В к А.
Касательное ускорение 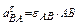 известно только по направлению (перпендикулярно нормальному), а модель найти пока не имеем возможности, так как неизвестно угловое ускорение шатуна АВ.
известно только по направлению (перпендикулярно нормальному), а модель найти пока не имеем возможности, так как неизвестно угловое ускорение шатуна АВ.
Строим многоугольник ускорений. При этом воспользуемся тем, что прямая, по которой направлено ускорение 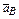 , известна.
, известна.
Ползун В движется по горизонтальной прямой, вдоль которой направлено и ускорение точки В. Отложим из точки В последовательно векторы 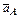 и
и 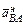 . Через конец вектора
. Через конец вектора 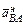 проведём прямую, перпендикулярную
проведём прямую, перпендикулярную 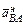 до пересечения её с прямой, по которой направлено ускорение
до пересечения её с прямой, по которой направлено ускорение 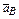 .
.

Проектируя векторное равенство на оси х и у, получаем
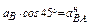 ;
; 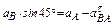 .
.
Из этих уравнений найдём аВ и 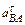 :
:
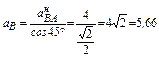 м/с2;
м/с2;
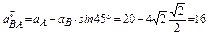 м/с2.
м/с2.
3. Нахождение углового ускорения звена АВ.
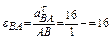 рад/с2.
рад/с2.
Ответ: 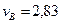 м/с2,
м/с2, 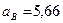 м/с2,
м/с2, 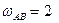 рад/с,
рад/с, 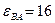 рад/с2.
рад/с2.
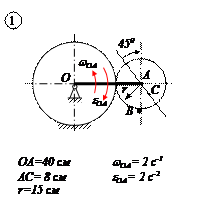
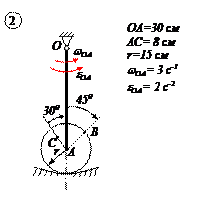
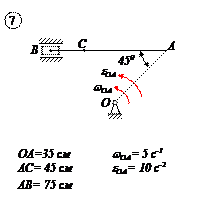
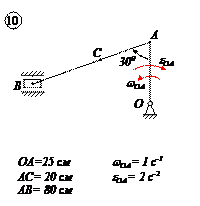
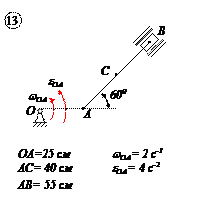
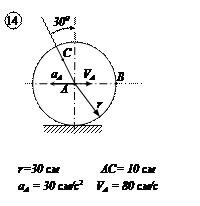
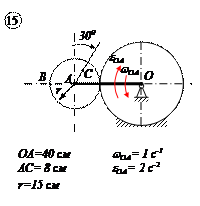
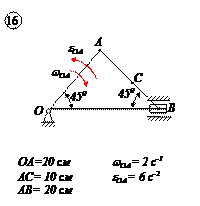
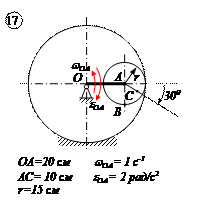
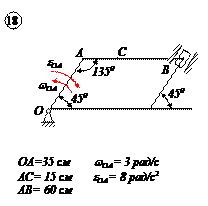
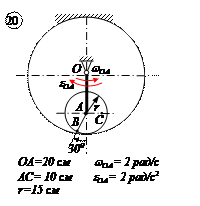
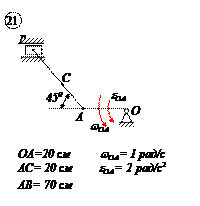
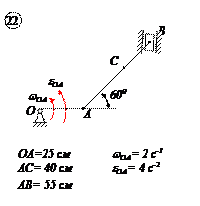
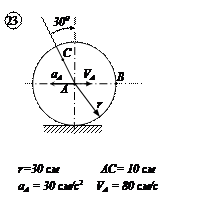
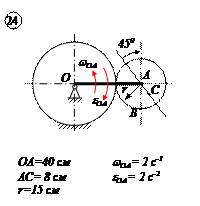
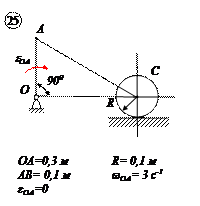
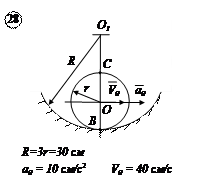
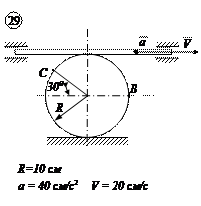
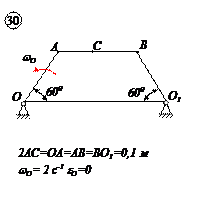
Варианты задачи 4.
| 
|
| 
|
| 
|
| 
|
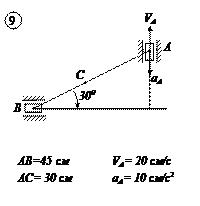
| 
|
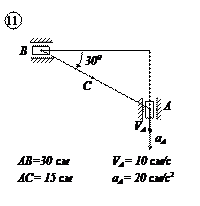
| 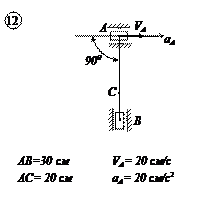
|
| 
|
| 
|
| 
|
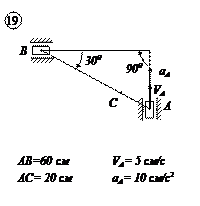
| 
|
| 
|
| 
|
| 
|
 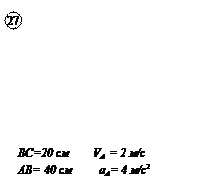
| 
|
| 
|
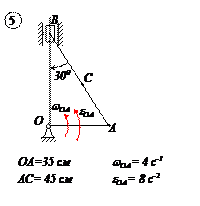
ЗАДАЧА №5
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
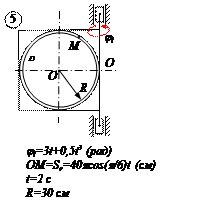
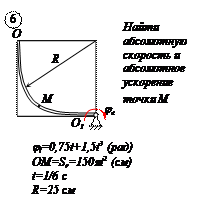
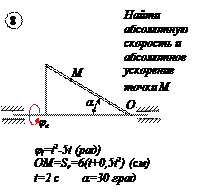
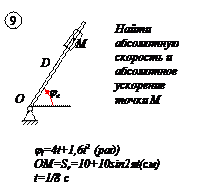
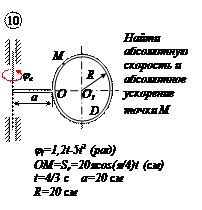
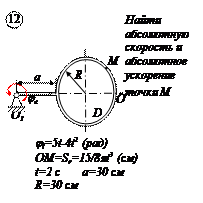
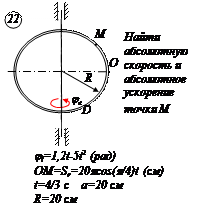
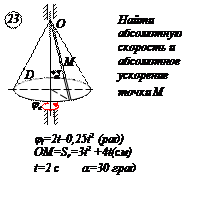
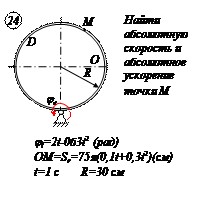
По заданным равнением относительного движения точки М неровного движения тела Д определить для момента времени 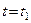 абсолютную скорость и абсолютное ускорение точки М.
абсолютную скорость и абсолютное ускорение точки М.
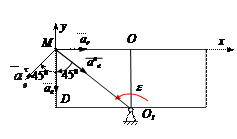
ПРИМЕР
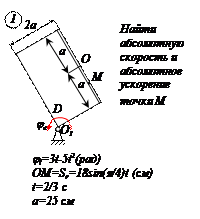
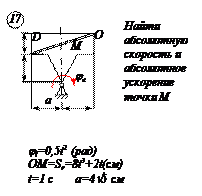
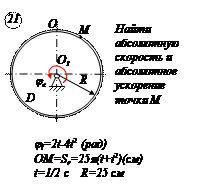
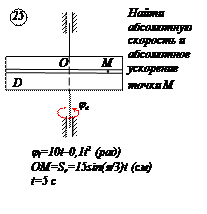
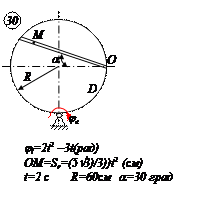
Прямоугольная пластина Д вращается вокруг неподвижной оси, проходящей через точку А, по закону 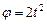 (рад)
(рад)
В пластине вдоль прямой АВ движется точка М. закон её относительного движения задан уравнением 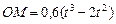
(В в метрах,t– в секундах)
Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t=1с.
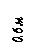
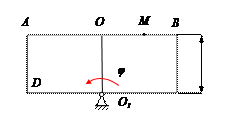
РЕШЕНИЕ
Находим положение точки М в момент времени t1:
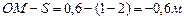
Отрезок ОМ =0,6 м откладываем в лево от точки 0,поскольку на отрезке показана точка М при положительных значениях ОМ от точки 0.
Абсолютную скорость точки М найдём как геометрическую сумму относительной и переносной скоростей:

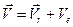
Модуль относительной скорости
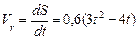 .
.
При t=1c 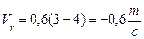
Направление 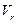 указано на рисунке, при этом учтен знак«минус».
указано на рисунке, при этом учтен знак«минус».
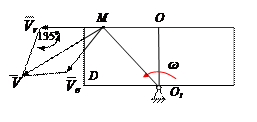
Модуль переносной скорости 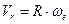
где 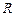 –радиус траектории точки М в переносном движении относительно О1 который можно найти по теореме Пифагора,
–радиус траектории точки М в переносном движении относительно О1 который можно найти по теореме Пифагора,
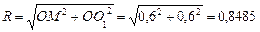 м;
м;
ω–угловая скорость тела,
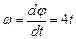
При 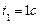 ω=4
ω=4 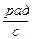
Теперь посчитаем 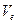 .
.
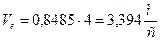
Направление 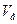 перпендикулярно МО1(см. рисунок).
перпендикулярно МО1(см. рисунок).
Абсолютную скорость 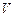 можно найти или через её проекции оси Х и У или по теореме косинусов.
можно найти или через её проекции оси Х и У или по теореме косинусов.
Остановимся на втором варианте.
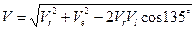
При 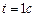
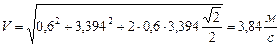
Абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориорисова ускорений:
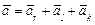
Модуль относительного ускорения
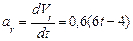
При 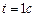
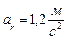
Переносное ускорение равно геометрической сумме нормальной касательной составляющих:
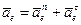 .
.
Модуль нормальной составляющей 
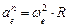
При 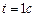
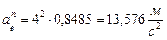
Касательное ускорение 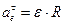 ,
,
Где 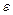 – угловое ускорение тела.
– угловое ускорение тела.
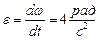
При 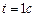
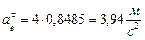
Колирисово ускорение находится по формуле
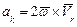
Модуль этого ускорения
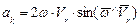
Так как 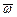 направлен по оси вращения, т.е. перпендикулярно плоскости рисунка «к нам», а
направлен по оси вращения, т.е. перпендикулярно плоскости рисунка «к нам», а 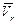 лежит в этой плоскости, то
лежит в этой плоскости, то
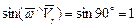
При 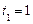
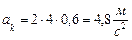
Направление 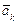 находим по правилам векторного произведения.
находим по правилам векторного произведения.
Покажем направления составляющих абсолютного ускорения на рисунке.
Модуль абсолютного ускорения точки М находим через проекции:
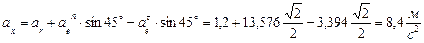
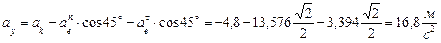
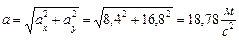
Ответ: при 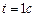
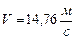 ;
; 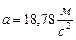
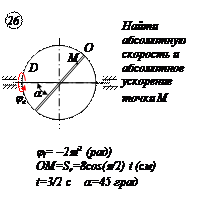
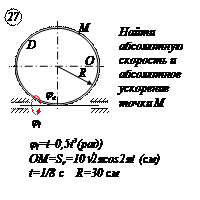
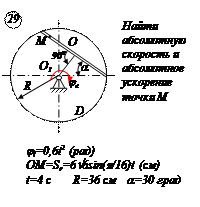
Варианты задачи 5.
| G 
| ||
  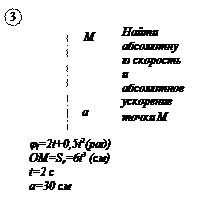
| 
| ||
| 
| ||

| 
| ||
| 
| ||
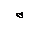 
| 
|

| 
| ||

|
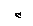 
| ||
| 
| ||
|  
| ||
| 
| ||
| 
| ||
| 
| ||
|

| ||
| 
|
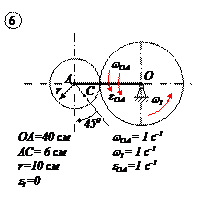
ЗАДАЧА №6
ДИНАМИКА ТОЧКИ
Груз D массой m,получив в точке А начальную скорость 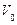 ,движется по изогнутой трубе АВС, расположенной в вертикальной плоскости.
,движется по изогнутой трубе АВС, расположенной в вертикальной плоскости.
На участке АВ на груз, кроме силы тяжести действуют сила сопротивления среды 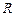 , зависящая от скорости
, зависящая от скорости 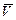 груза (направлена против движения).
груза (направлена против движения).
В точки В груз не изменяя величины своей скорости переходит на участок ВС трубы, где на него, помимо силы тяжести действует сила трения (коэффициент трения груза о трубу f=0.2) и переменная силаF, проекция которой Fx на ось Х задаётся.
Считая груз материальной точкой и зная расстояние АВ= l или время t 1 движения груза от точки А до точки В,найти закон движения груза на участке ВС, т.е. ВД=Х(t)
Примечание: каждый рисунок относится к двум вариантам задачи.
Пример. На участке АВ на груз D действует постоянная сила 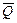 ,направление которой показано на рисунке, и сила сопротивления
,направление которой показано на рисунке, и сила сопротивления 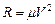 .движение от точки А до точки В длиться t1c. На участке ВС на грузе действует сила трения F (коэффициент трения f=0.1)и переменная сила
.движение от точки А до точки В длиться t1c. На участке ВС на грузе действует сила трения F (коэффициент трения f=0.1)и переменная сила 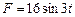 , где F измеряется в ньютонах, а t в секундах.
, где F измеряется в ньютонах, а t в секундах.
Определить закон движения груза на участке ВС при следующих условиях:m=8 кг, Q=20 Н, 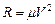 ,где μ=0,2
,где μ=0,2 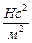 ,V0=0, t=2c.
,V0=0, t=2c.
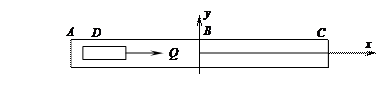
РЕШЕНИЕ
1.рассотрим движение груза на участке АВ. Составим дифференциальное уравнение движения на этом участке:
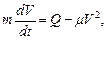
или 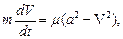
где для сокращения записей введено обозначения 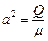 .
.
Разделив переменную и интегрируя обе части равенства, получим
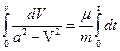 ;
;
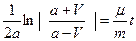 .
.
Из последнего выражения найдем V:
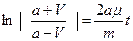 ;
; 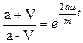 ;
;
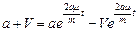 ;
;
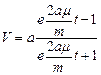 .
.
Учитывая, что 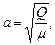 находим
находим
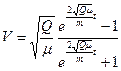 .
.
Пологая 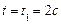 ,определяем скорость в точки В:
,определяем скорость в точки В:
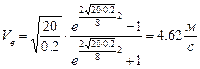 .
.
- теперь рассмотрим движение груза на участке ВС. Найденная скорость Vв будет для движения на этом участке начальной скоростью.
Составим дифференциальные уравнение движение груза:
 ,
,
где 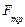 –сила трения;
–сила трения; 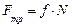 ;
; 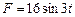
для горизонтального участка сила нормального давления груза на трубу 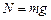 .в случае если участок наклонён к горизонту на угол
.в случае если участок наклонён к горизонту на угол 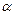 ,
, 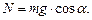
Разделим правую и левую части дифференциального уравнения на  получаем
получаем
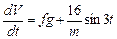
Умножим правую и левую части на 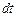 и проинтегрируем полученное выражение:
и проинтегрируем полученное выражение:
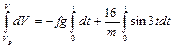 ;
; 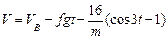 ,
,
или 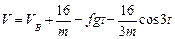 .
.
Выразим скорость груза через производную от координаты Х:
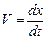 ;
;
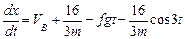 .
.
Умножим правую и левую части на 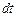 и возьмём интегралы от обеих частей:
и возьмём интегралы от обеих частей:
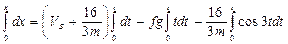 ;<
;<






