Що в ло­гі­ці пре­ди­ка­тів вва­жа­ють фо­р­му­лою?

11. Які вхо­джен­ня змін­них у фо­р­му­ли ло­гі­ки пре­ди­ка­тів на­зи­ва­ють зв'я­за­ни­ми і ві­ль­ни­ми?

12. Для ко­ж­но­го ква­н­то­ра ви­зна­ч­те об­ласть йо­го дії; для ко­ж­ної змін­ної вка­жіть її ві­ль­ні та зв'я­за­ні вхо­джен­ня.

(а) "х(Рх É Qx);

(б) "x(Рх É Qx) & $уRхy;

(в) "x((PxÉQy) v $ yRxy);

(г) $x"у(Gxy v «xPyxz);

(д) "х(РхÉ $у(Qy & Rxy));

(е) "х"уР­ху É Qxz.

13. Оха­ра­к­те­ри­зуй­те по­нят­тя „ за­к­ри­та фо­р­му­ла ” і „ ві­д­к­ри­та фо­р­му­ла ”.

14. Ви­зна­ч­те, які із пе­ре­лі­че­них ви­ра­зів є фо­р­му­ла­ми ло­гі­ки пре­ди­ка­тів. Пі­с­ля цьо­го вста­но­віть фо­р­му­ли, що є си­м­во­лі­ч­ни­ми за­пи­са­ми ви­сло­в­лю­вань, і фо­р­му­ли, що є си­м­во­лі­ч­ни­ми за­пи­са­ми про­по­зи­цій­них форм. По­яс­ніть свій ви­бір.

(а) $x₁P₁² x₁x₂ É "x₂(P₁¹x₂ v P₁²x₁x₂);

(б) "x₁P₁² x₁ v Q₁²x₁x₂;

(в) "x₁$x₂(P₁²x₁x₂ & ("x₂Q₁¹x₂ v (P₁¹a₁ É ~ Q₂²x₁a₂)));

(г) "x₁ É (P₁¹a v Q₁¹x₁).

15. Яку си­ту­а­цію на­зи­ва­ють ко­лі­зі­єю змін­них?

16. Яким чи­ном ква­н­то­ри за­га­ль­но­сті та іс­ну­ван­ня мо­ж­на ­тлу­ма­чи­ти за до­по­мо­гою ло­гі­ч­них спо­лу­ч­ни­ків кон'­ю­н­к­ції і ди­з'ю­н­к­ції?

17. Оха­ра­к­те­ри­зуй­те уні­вер­са­ль­не та ек­зи­с­те­н­цій­не роз­ши­рен­ня фо­р­мул ло­гі­ки пре­ди­ка­тів.

18. Сфо­р­му­люй­те роз­ши­рен­ня на­ве­де­них фо­р­мул (1)-(10) для уні­вер­су­мів U: а) {а}; б) {a, b}; в) {a, b, c}.

(1) "xKx;

(2) $хКх & Р;

(3) "хKx É $xGx;

(4) "x(Gx«P) v "хНх;

(5) На v $хGх;

(6) $x(Kx v Hx);

(7) "хКх «$х(Кх & ~Нх);

(8) ~"x(Kx & Gx);

(9) ~"хКx & ~"xGx;

(10) ~("xGx «$ x(Hx & ~Kx)).

19. Се­ред за­про­по­но­ва­них двох мно­жин ви­сло­в­лю­вань укра­ї­н­сь­кої мо­ви і фо­р­мул ло­гі­ки пре­ди­ка­тів від­шу­кай­те від­по­ві­д­ні па­ри ко­ре­к­т­них пе­ре­к­ла­дів:

(а) „Всі су­д­ді — юри­с­ти” (Gx, Lx);

(б) „Де­я­кі юри­с­ти — ша­х­ра­ї” (Sx);

(в) „Жо­д­ний су­д­дя не є ша­х­ра­єм”;

(г) „Де­я­кі су­д­ді — ста­рі за ві­ком, про­те — жва­ві” (Ох,Vx);

(д) „Су­д­дя Джонс не ста­рий і не жва­вий” (j);

(е) „Не всі юри­с­ти — су­д­ді”;

(є) „Де­я­кі юри­с­ти, що є по­лі­ти­ка­ми, — чле­ни па­р­ла­ме­н­ту” (Рх,Сх);

(ж) „Жо­ден член па­р­ла­ме­н­ту не є жва­вим”;

(з) „Всі ста­рі чле­ни па­р­ла­ме­н­ту — юри­с­ти”;

(и) „Де­я­кі жі­н­ки вод­но­час є юри­с­та­ми і чле­на­ми па­р­ла­ме­н­ту” (Wx);

(і) „Жо­д­на жі­н­ка не є вод­но­час по­лі­ти­ком і ха­т­ньою го­с­по­ди­не­ю” (Hx),

(ї) „Де­я­кі жі­н­ки-­юри­с­ти є ха­т­ні­ми го­с­по­ди­ня­ми”;

(й) „Всі жі­н­ки-­юри­с­ти обо­ж­ню­ють яко­гось су­д­дю” (Аху);

(к) „Де­я­кі юри­с­ти обо­ж­ню­ють ли­ше су­д­дів”;

(л) „Де­я­кі юри­с­ти обо­ж­ню­ють жі­нок”;

(м) „Де­я­кі ша­х­раї не обо­ж­ню­ють жо­д­но­го юри­с­та”;

(н) „Су­д­дя Джонс не обо­ж­нює жо­д­но­го ша­х­ра­я”;

(о) „І­с­ну­ють як юри­с­ти, так і ша­х­раї, що обо­ж­ню­ють су­д­дю Джо­н­са”;

(п) „Ті­ль­ки су­д­ді обо­ж­ню­ють су­д­дів”;

(р) „Всі су­д­ді обо­ж­ню­ють ли­ше су­д­дів”.

***

(а) $x(Wx& Сх& Lx);

(6) ~Oj &~Vj;

(в) "х(Gx É ~Sx);

(г) $x(Wx &Lx & Нх);

(д) "x(Ajx É ~ Sx);

(е) "x(Gx É Lx);

(є) ~"x(Lx É Gx);

(ж) "x((Cx & Ox) É Lx);

(з) $x(Lx & Sx);

(u) $x(Lx & Px &Cx);

(і) "x(Wx É ~(Px & Hx));

(ї) "x(Cx É ~"x);

(й) $x(Gx & Ox & Vx);

(к) "x"y((Ayx & Gx) É Gy);

(л) $x(Sx & " y(Axy É ~Ly));

(м) $х$у(Lx &Sy & Axj & Ayj);

(н) "x((Wx & Lx) É $ y(Gy & Axy));

(o) $x(Lx & $y(Wy & Axy));

(n) "x(Gx É " y(Axy É Gy));

(p) $x(Lx & " y(Axy É Gy)).

20. Здій­с­ніть пе­ре­к­лад ви­сло­в­лю­вань за до­по­мо­гою ба­га­то­мі­с­ного пре­ди­ката:

(а) „Андрій шанує Олега”;

(б) „Х­тось шанує Олега”;

(в) „Андрій шанує когось”;

(г) „Олег шанує усіх”;

(д) „У­сі шанують Олега”;

(е) „Х­тось шанує когось”;

(є) „Де­х­то шанує усіх”;

(ж) „У­сі шанують когось”;

(з) „Кожен шанує кожного”;

(и) „Ко­ж­ен шанує се­бе”;

(і) „Де­х­то шанує се­бе”;

(ї) „Ні­х­то не шанує се­бе”;

(й) „Де­х­то не шанує се­бе”;

(к) „Де­х­то не шанує нікого”.

21. Здій­с­ніть пе­ре­к­лад ви­сло­в­лю­вань на мо­ву ло­гі­ки пре­ди­ка­тів:

(а) „Всі олені - сса­в­ці”;

(б) „Де­я­кі аку­ли - без­пе­ч­ні”;

(в) „Жо­д­на ри­ба не є те­п­ло­кро­в­но­ю”;

(г) „Не всі ри­би без­пе­ч­ні”;

(д) „Ре­п­ти­лії і ам­фі­бії не є те­п­ло­кро­в­ни­ми”;

(е) „Де­я­кі при­ма­ти і гри­зу­ни жи­вуть на де­ре­вах”;

(є) „Ті­ль­ки пта­хи лі­та­ють”;

(ж) „Се­ред па­ву­ків ли­ше та­ран­ту­ли і чо­р­ні вдо­ви от­руй­ні”;

(з) „Всі су­м­ча­с­ті (і тіль­ки во­ни) ма­ють ‘ки­ше­ню’ ”;

(и) „Де­я­кі ор­га­ні­з­ми є хре­бе­т­ни­ми, а де­які - мо­лю­с­ка­ми, але жо­д­ний ор­га­

нізм не є хре­бе­т­ним і мо­лю­с­ком вод­но­час”;

(і) „Ні­х­то, окрім дво­но­гих, не є ро­зу­м­ним”;

(ї) „Тва­ри­ни по­во­дять­ся спо­кій­но, як­що за ни­ми не слід­ку­ють”;

(й) „Тва­ри­ни по­во­дять­ся спо­кій­но, тіль­ки як­що за ни­ми не слід­ку­ють”;

(к) „Де­я­кі аку­ли - без­пе­ч­ні ри­би, але не всі без­пе­ч­ні ри­би є аку­ла­ми”;

(л) „Я­к­що Флі­пер - дель­фін і всі дель­фі­ни сса­в­ці, то­ді Флі­пер - сса­вець”;

(м) „Жо­д­ний го­ро­бець не бу­дує гні­з­да, до­ки не знай­де со­бі па­ру”;

(н) „Жо­д­ний хи­жак не є тра­во­їд­ним”;

(о) „Сса­вець із кри­ла­ми - це ле­тю­ча ми­ша”;

(п) „Сса­вець, що має кри­ла - лі­та­є”;

(р) „Жо­д­на ри­ба не має крил, як­що во­на не на­ле­жить до сі­м'ї Exocoetidae”;

(с) „Жо­д­ний без­зу­бий ор­га­нізм не є хи­жа­ком”;

(т) „Не всі хи­жа­ки - м'я­со­їд­ні”;

(у) „І­с­нує ре­п­ти­лія, яка ме­н­ша за со­ба­ку, але бі­ль­ша за ко­та”;

(ф) „Де­я­кі ри­би пла­ва­ють по­ві­ль­ні­ше, ніж лю­ди”;

(х) „І­с­нує та­ка ма­в­па, яка до­гля­дає за всі­ма (і ли­ше та­ки­ми) ма­в­па­ми, що са­мі

за со­бою не до­гля­да­ють”.

Семінар 7 (2 год.)

22. Вста­но­віть, чи бу­дуть фо­р­му­ли (1)-(10) із впра­ви 18 іс­тин­ни­ми за умо­ви ін­тер­пре­та­цій:

(а) U: {а}, К: {a}, G: {}, H: { }, Р- хи­б­не;

(б) U: {a, b}, K: {a}, G: {а, Ь], Н: { }, Р- іс­тин­не;

(в) U: {а, Ь, с}, К: (a, b, c}, G: {a, b}, H: {b}, P- хи­б­не.

23. Яку фо­р­му­лу ло­гі­ки пре­ди­ка­тів вва­жа­ють за­га­ль­но­зна­чу­щою?

24. Здій­с­ніть символізацію за­зна­че­них мі­р­ку­вань за допомогою мо­ву ло­гі­ки пре­ди­ка­тів і, використовуючи ме­то­д ана­лі­ти­ч­них таб­лиць, до­ве­діть, що міркування є правильними:

(а) „Том - кіт. Усі ко­ти - ро­зу­м­ні. От­же, Том - ро­зу­м­ний” (‘m’, ‘B’, ‘D’);

(б) „Том - ро­зу­м­ний. Жо­д­ний кіт не є ро­зу­м­ним. От­же, Том - не кіт”;

(в) „Том - не кіт. Ли­ше ко­ти від­да­ні. От­же, Том - не від­да­ний”;

(г) „У­сі лі­ка­рі-­чо­ло­ві­ки - дбай­ли­ві. Ва­силь - не дбай­ли­вий. Ва­силь - чо­ло­вік. От­же, Ва­силь - не лі­кар”. (‘M’, ‘N’, ‘S’, ‘n’).

(д) „У­сі фра­н­цу­зи, за ви­клю­чен­ням ме­ш­ка­н­ців Па­ри­жа, лю­б'я­з­ні.

Жак - фра­н­цуз. Жак - не лю­б'я­з­ний. От­же, Жак - ме­ш­ка­нець Па­ри­жа” (‘G’, ‘Р’, 'K’, ‘a’).

25. (1) За до­по­мо­гою ме­то­ду ана­лі­ти­ч­них таб­лиць до­ве­діть:

(а) ["x(Kx É Gx) & "x(Gx É ~Hх)] |= "x(Kx É ~Нх);

(б) ["x(Kx É ~Gx) & "x(Hx É Gх)] |= "x(Kx É ~Нх);

(в) ["x(K xÉ Gx) & "x(Hx É ~Gх)] |= "x(Kx É ~Нх);

(г) ["x(Gx É ~Kx) & "x(Hx É Gх)] |= "x(Kx É ~Нх);

(д) "х(Кх É Gx) |= ("хKx É "xGx);

(е) ["х((Кх v Gx) É Нх) & " х~Нх] |= "х~Кх.

(2) Для ко­ж­но­го із на­ве­де­них ни­ж­че мі­р­ку­вань ви­бе­ріть (се­ред за­про­по­но­ва­но­го у п.(1) пе­ре­лі­ку) пе­в­ну фо­р­му­лу, яка від­повідає йо­го ло­гі­ч­ній фо­р­мі:

(а) „Жо­д­ний ні­мець не є фра­н­цу­зом. Всі ба­ва­р­ці - ні­м­ці. От­же, жо­д­ний фра­н­цуз не є ба­ва­р­цем”;

(б) „Жо­д­ний фра­н­цуз не п'є пи­во. Всі ба­ва­р­ці п'ють пи­во. От­же, жо­д­ний фра­н­цуз не є ба­ва­р­цем”;

(в) „У­сі ба­ва­р­ці п'ють пи­во. Жо­ден фра­н­цуз не п'є пи­во. От­же, жо­д­ний ба­ва­рець не є фра­н­цу­зом”;

(г) „У­сі ні­м­ці - па­т­рі­о­ти. Жо­д­ний па­т­рі­от не є не­щи­рим. От­же, жо­д­ний ні­мець не є не­щи­рим”.

26. Здій­с­ніть символізацію за­зна­че­них мі­р­ку­вань за допомогою мо­ву ло­гі­ки пре­ди­ка­тів і, використовуючи ме­то­д ана­лі­ти­ч­них таб­лиць, до­ве­діть, що міркування є правильними:

(а) „Я­к­що ко­ж­ний ро­зу­м­ний фі­ло­соф - ци­нік і ли­ше жі­н­ки є ро­зу­м­ни­ми фі­ло­со­фа­ми, то то­ді, як­що іс­ну­ють ро­зу­м­ні фі­ло­со­фи, де­які жі­н­ки - ци­ні­ки”.

(б) „Де­я­кі ре­с­пу­б­лі­ка­н­ці лю­б­лять усіх де­мо­к­ра­тів. Жо­ден ре­с­пу­б­лі­ка­нець не лю­бить жо­д­но­го со­ці­а­лі­с­та. От­же, жо­ден де­мо­к­рат не є со­ці­а­лі­с­том”.

(в) „Я­к­що йде дощ, жо­д­на пта­ш­ка не є ща­с­ли­во­ю. Як­що йде сніг, де­які пта­ш­ки - ща­с­ли­ві. От­же, те, що сніг не йде, є не­об­хід­ною умо­вою для то­го, щоб йшов дощ” (по­зна­ч­те ‘дощ іде’ про­по­зи­цій­ною змін­ною p, а ‘сніг іде’ - q).

27. До­ве­діть, що:

(а) ~"х(Кх É Gx) & "х(Нх É Gx) |= $х~Нх;

(б) "x(Kx É p) & ~p |= "х~Kх;

(в) "x(Hxz É Нах) & Наz |= Наа;

(г) "х(Кх «Gx) & Ga |= $уКу;

(д) "x(Kx «Gx) & ~$y~Gy |= Kb;

28. До­ве­діть, що за­про­по­но­ва­ні ви­ра­зи не бу­дуть пра­ви­ль­ни­ми (по­бу­дуй­те роз­ши­рен­ня ква­н­то­р­них фо­р­мул для уні­вер­су­му U:{а,Ь} і знайдіть від­по­ві­д­ні контр­мо­де­лі):

(1) "xKx É"xGx |="x(Kx É Gx);

(2) $хКх É $ xGx |= "х(Кх É Gx);

(3) $хКх & $ xGx |= $х(Кх & Gx);

(4) $х(Кх v Gx) |= "xKx v "xGx;

(5) $х(Кх É Gx) |= $хКх É $xGx;

(6) $х(Кх É Gx) |= "хКх É "xGx;

(7) "xKx «"xGx |="x(Kx «Gx);

(8) $xKx «$xGx |="x(Kx «Gx);

(9) "xKx «p |= "x(Kx «p);

(10) $xKx «p |= "x(Kx «p);

(11) $x(Kx «p) |= $xKx «p;

(12) $x(Kx «p) |= "xKx «p.

29. Вста­но­віть пра­ви­ль­ність мі­р­ку­ван­ня:

(а) „Ко­ж­ний лі­н­г­віст зне­ва­жає де­яко­го фі­ло­со­фа, який кри­ти­ку­вав Хом­сь­ко­го. Хом­сь­кий — лі­н­г­віст. Ко­ж­ний фі­ло­соф, який кри­ти­ку­вав лі­н­г­ві­с­та — по­зи­ти­віст. От­же, ко­ж­ний лі­н­г­віст зне­ва­жає де­яко­го по­зи­ти­ві­с­та”.

(б) „І­с­нує хтось, хто го­то­вий за­пла­ти­ти за всі кви­т­ки. От­же, за ко­ж­ний кви­ток хтось го­то­вий за­пла­ти­ти” (по­зна­чення: ‘бу­ти лю­ди­но­ю’ - Р, ‘бу­ти кви­т­ком’ - В, ‘х го­то­вий за­пла­ти­ти за у’ - Gxy).

(в) „Ко­ж­ний, хто ку­пив кви­ток, отри­мує пре­мі­ю. От­же, як­що пре­мій не­має, то ні­хто не ку­пу­вав кви­т­ки” (по­зна­чення: ‘бу­ти кви­т­ком’ - G, ‘бу­ти пре­міє­ю’ - Р, ‘х ку­пує у’ - Вху, ‘х отри­мує у’ - Rxy).

(г) „У­сі ві­в­ці тва­ри­ни. От­же, усі го­ло­ви овець є го­ло­ва­ми тва­рин” (по­зна­ч­ення: ‘бу­ти ві­в­це­ю’ - Р, ‘бу­ти тва­ри­но­ю’ - G, ‘х є го­ло­вою у’ - Нху).

(д) „Кит — сса­вець. Де­які ри­би — сса­в­ці. Усі ри­би ма­ють хвіст. От­же, де­які хво­с­ти риб є хво­с­та­ми сса­в­ців” (по­зна­чення: ‘а є хво­с­том b’ - Hab).

(е) „Я­к­що ко­ж­ний роз­мо­в­ляє із ко­ж­ним, то­ді хтось по­зна­йо­мив їх. Ні­хто' не зна­йо­мить будь-­ко­го із будь-­ким, як­що він' їх обох не зна­є. Ко­жен роз­мо­в­ляє з Ос­та­пом. От­же, ко­ж­но­го зна­йо­мить з Ос­та­пом хтось, хто йо­го (Ос­та­па) зна­є” (по­зна­ч­ення: ‘а зна­йо­мить b і с’ - IаЬс, ‘а роз­мо­в­ляє із b’ - Pab, ‘а знає b’ - Gab, ‘Ос­тап’ – m).

30. Користуючись предикатом тотожності, символізуйте висловлювання:

(а) Наявні принаймні три помилки.

(б) Наявні щонайбільше три помилки.

(в) Наявні точно три помилки.

(г) Більше двох людей помітили помилку.

(д) Усі, за виключенням Андрія, пішли.

(е) Ніхто, окрім Юрія, не знає.

(є) Андрій співав, а хтось інший (хтось іще) роздивлявся навкруги.

(ж) Петро поважає тільки себе.

(з) Петро поважає якусь іншу людину.

(и) Лише Еверест варто підкорювати.

(і) Людей, які люблять тільки себе, не люблять інші люди.

31. Символізуйте запропоноване міркування і за допомогою методу аналітичних таблиць доведіть його правильність: «Існує щонайбільше дві розумні людини і принаймні два генії. Усі генії розумні. Отже, є точно дві розумні людини».

32. Доведіть, що відношення не може бути:

(а) інтранзитивним і рефлексивним;

(б) асиметричним і нерефлексивним;

(в) транзитивним, рефлексивним і асиметричним;

(г) транзитивним, несиметричним і іррефлексивним.

 

ТЕМА 4

Семінар 8 (2 год.)

1. Які висловлювання (і чому) називають „ категоричними” („атрибутивними”, „асерторичними”, „немодалізованими”)?

2. Визначіть, які вирази (серед запропонованих) є категоричними висловлюваннями:

(а) „Котра година?”;

(б) „Цей хлопець не має ніякої суспільної вартості, він просто індивід”;

(в) „Усі люди є вільні і рівні у своїй гідності та правах”;

(г) „В салоні літака палити заборонено”;

(д) „Прошу вибачення”;

(е) „Знайди свій власний світ”;

(є) „Бог не без милості, а козак не без долі”.

3. Охарактеризуйте структурну будову простих категоричних висловлювань. Наведіть відповідні приклади.

4. Які існують види простих категоричних висловлювань?

5. До якого типу простих категоричних висловлювань (А, Е, І, О) належать висловлювання:

(а) „Існують посмішки, що заставляють бліднути”;

(б) „Жодна робота, в якій відсутні нові ідеї, не заслуговує на премію”;

(в) „Не все є золотом, що блищить”;

(г) „Надія помирає останньою”;

(д) „Інколи потяги запізнюються”;

(е) „Усі щасливі люди – добрі”.

6. За допомогою діаграм Венна зобразіть відношення між S i P у висловлюваннях А,Е,І,О.

7. Для пунктів (1)-(7) запропонованої діаграми сформулюйте відповідні твердження:

 

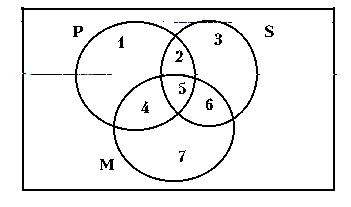
(1) Предмети, які є Р, але не є S і не є М;

(2) Предмети, які є Р і S, але не є М;

(3)..........

(4)..........

(5)..........

(6)..........

(7)..........

(8)..........

8. За допомогою діаграм Венна виразіть:

(а) Щось є D і не є С;

(б) Лише D є С;

(в) Ніщо не є D і щось є С;

(г) Щось не є С і не є D;

(д) Ніщо не є не-С і не є не-D;

(е) Усе є або D, або С;

(є) Усе є або D, або С і ніщо не є одноразово D і С;

(ж) Усі і лише С є D.

9. За допомогою діаграм Венна (на діаграмі використовуйте S-коло, М-коло і Р-коло) виразіть:

(а) „Жодне S не є М”;

(б) „Кожне М є S”;

(в) „Деякі Р є М і S”;

(г) „Лише S є Р”;

(д) „Деякі Р є М або S”;

(е) „Лише Р існують”.

10. Чи будуть правильними міркування:

(а) „Деякі S є Р. Отже, існують Р”;

(б) „Не існує (жодного) S. Отже, жодне S не є Р”.

Дайте відповідь за допомогою діаграм Венна.

11. Чи випливають висловлювання А, Е, І, О із засновку „Не існує (жодного) Р”. Дайте відповідь за допомогою діаграм Венна.

12. За допомогою діаграми Венна репрезентуйте твердження: „Ніхто, окрім хоробрих, не заслуговує на славу” (позначте: „S” – „хоробрі (люди)”, „Р” – „ті, хто заслуговує на славу”).

13. Які три групи законів досліджує традиційна теорія силогістики.

14. Сформулюйте закони логічного квадрату.

15. За допомогою законів логічного квадрату отримайте усі можливі висновки із запропонованих засновків:

(а) „Усі студенти складають іспити”;

(б) „Не кожний студент складає іспити успішно”;

(в) „Деякі студенти не з'являються на іспити”;

(г) „Невірно, що деякі студенти не з'являються на іспит без поважної причини”;

(д) „Деякі студенти складають іспити не зі своєю группою”;

(е) „Невірно, що існують студенти, які знають предмет краще, ніж екзаменатор”;

(є) „Жодний студент не звільняється від складання іспитів”;

(ж) „Невірно, що жоден студент не може закінчити курс екстерном”.

16. За допомогою законів „логічного квадрату” встановіть наявність/відсутність відношення логічного слідування між висловлюваннями у міркуваннях:

(а) З істинності висловлювання: „Не всі книги цікаві” випливає хибність висловлювання: „Жодна книга не є цікавою”;

(б) З хибності висловлювання: „Не всі книги цікаві” випливає хибність висловлювання: „Жодна книга не є цікавою”;

(в) З істинності висловлювання: „Не всі книги цікаві” випливає істинність висловлювання: „Невірно, що деякі книги цікаві”;

(г) З істинності висловлювання: „Жоден лев не є травоїдним” випливає істинність висловлювання: „Деяі леви не є травоїдними”;

(д) З істинності висловлювання: „Не кожна аморальна дія є протиправною” випливає хибність висловлювання: „Жодна аморальна дія не є протиправною”;

(е) З хибності висловлювання: „Не кожна аморальна дія є протиправною” випливає хибність висловлювання: „Жодна аморальна дія не є протиправною”;

(є) З істинності висловлювання: „Не кожна аморальна дія є протиправною” випливає істинність висловлювання: „Деякі аморальні дії – протиправні”;

(ж) З істинності висловлювання:„Деякі аморальні дії не є протиправними” випливає хибність висловлювання: „Кожна аморальна дія є протиправною”;

(з) З хибності висловлювання: „Жодна аморальна дія не є протиправною” випливає хибність висловлювання: „Всі аморальні дії – протиправні”;

(и) З істинності висловлювання: „Жодна аморальна дія не є протиправною” випливає істинність висловлювання: „Деякі аморальні дії не є протиправними”;

(і) З істинності висловлювання:„Деякі аморальні дії є протиправними” випливає істинність висловлювання: „Деякі аморальні дії не є протиправними”.

17. Чи будуть правильними міркування:

(а) „Невірно, що деякі іспити є важливими; отже, невірно, що усі іспити важливі”;

(б) „Невірно, що деякі іспити є важливими; отже, усі іспити не є важливими”;

(в) „Деякі іспити - важливі; отже, деякі іспити не є важливими”;

(г) „Не всі іспити є важливими; отже, невірно, що жоден іспит не є важливим”;

(д) "Усі іспити - важливі; отже, невірно, що деякі іспити не є важливими".

18. В чому полягає логічний сенсоперацій: перетворення, обернення, протиставлення предикату, протиставлення суб'єкту?

19. Здійсніть перетворення, обернення, протиставлення предикату, протиставлення суб'єкту висловлювань:

(а) „Деякі шпигуни вчились в Оксфорді”;

(б) „Всі студенти – кмітливі”;

(в) „Жоден натуральне число не є ірраціональним”;

(г) „Деякі економічні кризи не спричинюють соціальну нестабільність”.

20. Встановіть вид безпосереднього умовиводу та його правильність:

(а) „Усі розповідні речення виражають судження. Отже, деякі речення, що виражають судження є розповідними”;

(б) „Деякі люди поважають закон. Отже, дехто серед тих, хто не поважає закон, не є Людиною”;

(в) „Жодна людина не є досконалою. Отже, усі недосконалі істоти є людьми”;

(г) „Жоден злочин не є справедливим. Отже, деякі несправедливі вчинки є злочином”;

(д) „Деякі люди міркують логічно. Отже, дехто серед тих, хто міркує логічно є Людиною”;

(е) „Більшість державних службовців не беруть хабарів. Отже, деякі хабарники не є державними службовцями”;

(є) „Усі бізнесмени займаються благодійністю. Отже, жоден серед тих, хто не займається благодійністю, не є бізнесменом”.

 

Семінар 9 (1 год.)

21. Охарактеризуйте структурну будову простого категоричного силогізму.

22. Що таке „ фігура силогізму ”?

23. В чому полягає проблематичність четвертої фігури простого категоричного силогізму?

24. Що таке „ модус силогізму”?

25. Встановіть фігуру і модус силогізмів:

(а)

Всі люди смертні;

Всі греки - люди;

Всі греки смертні.

(б)

Жодна людина не є досконалою;

Усі греки - люди;

Жодний грек не є досконалим.

(в)

Всі філософи мудрі;

Деякі греки - філософи;

Деякі греки мудрі.

(г)

Жодний філософ не є злим;

Деякі греки - філософи;

Деякі греки не є злими.

(д)

Усі греки - люди;

Деякі смертні не є людьми;

Деякі смертні не є греками.

26. Які методи перевірки правильності модусів простого категоричного силогізму пропонує традиційна логіка? Охарактеризуйте семантичний метод модельних схем (діаграми Венна, діаграми Ейлера), синтаксичний метод загальних правил силогізму. Порівняйте переваги і недоліки зазначених методів.

27. Встановіть правильність модусів простого категоричного силогізму із вправи (25).

28. Встановіть, який силогістичний висновок випливає з кожної пари запропонованих засновків. Для кожної пари засновків, з якої неможливо виснувати силогістичний висновок, встановіть (за допомогою діаграмного методу), чи можливо, уводячи додатковий екзистенційний засновок все ж таки отримати силогістичний висновок.

 

 

(а)

Усі богохульники - злі;

Жодний святий не є богохульником;

..........

(б)

Жодна змія не літає;

Деякі змії отруйні;

..........

(в)

Жодна змія не літає;

Деякі птахи літають;

..........

(г)

Все, що цікавить мене викликає нудьгу у Петра;

Все, що цікавить Тетяну викликає нудьгу у Петра;

..........

(д)

Все, що цікавить мене викликає нудьгу у Петра;

Все, що цікавить Петра викликає нудьгу у Тетяни;

..........

(е)

Усі безкорисливі люди - щедрі;

Жодна скупа людина не є щедрою;

..........

(є)

Усі схильні до гарячковості люди - холерики;

Деякі оратори схильні до гарячковості;

..........

(ж)

Жоден банкрут не є багатим;

Деякі підприємці не є багатими;

..........

(з)

Жоденпрофесор не є невігласом;

Деякі невігласи - марнославні;

..........

(и)

Він дав мені десять доларів;

Я був щасливий;

..........

(і)

Усі блідолиці - флегматичні;

Лише блідолиці мають поетичну зовнішність;

..........

29. З якими складнощами матиме справу традиційна логіка, оцінюючи правильність міркування: „Якщо усі пошукачі, що отримали повідомлення - філологи, то деякі пошукачі повідомлення не отримали. Або усі пошукачі отримали повідомлення, або усі пошукачі - філологи. Отже, якщо усі пошукачі- філологи отримали повідомлення, тоді деякі пошукачі, що не є філологами отримали повідомлення”.

30. Перевірте правильність міркувань:

(а) „Усі розумні люди - чемні, а усі чемні люди - терплячі. Отже, лише терплячі люди – розумні”;

(б) „Усі вітаміни - дешеві. Лише дешеві продукти поживні. Отже, усі вітаміни – поживні”;

(в) „Деякі інтелігентні люди не є розсудливими, бо жоден егоїст не є розсудливим, а деякі інтелігентні люди – егоїсти”;

(г) „Лише чемні люди - розумні, але деякі чемні люди не є інтелігентними. Отже, деякі розумні люди не є інтелігентними”;

(д) „Деякі чемні люди не є розумними, бо жодна чемна людина не є агресивною, а деякі агресивні люди не є розумними”;

(е) „Усі слабкі люди схильні до брехні, а те, що Петро схильний до брехні свідчить, що він не є виключенням”;

(є) „Деякі найкращі учні району не отримали місця в гімназії, бо жоден серед тих, хто отримав місце в гімназії не був допущений до іспитів у ліцеї, але все ж таки деякі учні, що були допущені до іспитів в ліцеї - найкращі в районі”;

(ж) „Філософські праці Канта є складними і лише складні твори є важливими. Отже, філософські праці Канта є важливими”;

(з) „Невірно стверджувати, що преса назвала усіх делегатів безвідповідальними. Скоріше навпаки, бо не усі делегати голосували за одноденний страйк і лише ті, хто дійсно за це голосував були засуджені як безвідповідальні”;

(и) „Ви - не те, що я. Я - людина. Отже, ви - не людина”;

(і) „Усі жителі Києва - люди. Усі жителі Дарницького району міста Києва - люди. Отже, усі жителі Дарницького району міста Києва - жителі Києва”.

(ї) „Усі великі людиноподібні мавпи походять від нижчих форм життя. Люди також походять від нижчих форм життя. Отже, усі люди - великі людиноподібні мавпи”;

(ж) „Дехто серед тих, хто не вірить, що Бог створив світ за сім днів, не є фундаменталістом, але деякі фундаменталісти вірять, що Бог створив світ за сім днів. Отже, жоден серед тих, хто не вірить, що Бог створив світ за сім днів, не є фундаменталістом”;

31. Прокоментуйте текст з точки зору теорії простого категоричного силогізму:

Л о г і к (до Літнього Добродія). Ось, наприклад, такий силогізм. В кота чотири лапи. Ізидор і Фріко мають по чотири лапи кожен. Отже, Ізидор і Фріко - коти.

Л і т н і й Д о б р о д і й (до Логіка). В мого собаки теж чотири лапи.

Л о г і к (до Літнього Добродія). В такому разі це кіт. [...]

Л і т н і й Д о б р о д і й (до Логіка, після довгих роздумів). Отже, за логікою, мій пес буде котом.

Л о г і к (до Літнього Добродія). За логікою так. Але протилежне теж слушне. [...]

Л і т н і й Д о б р о д і й (до Логіка). Так, логіка річ чудова.

Л о г і к (до Літнього Добродія). Якщо не зловживати нею. [...]

Ще один силогізм: усі коти смертні. Сократ смертний. Отже, Сократ кіт.

Л і т н і й Д о б р о д і й. І в нього чотири лапи. Справді, в мене був кіт, що звався Сократом.

Л о г і к. Бачте. [...]

Л і т н і й Д о б р о д і й (до Логіка). Так, отже, Сократ був котом!

Л о г і к (до Літнього Добродія). І нам це з'ясувала логіка. [...]

Повернімось до наших котів.

Л і т н і й Д о б р о д і й (до Логіка). Я слухаю. [...]

Л о г і к (до Літнього Добродія). Кіт Ізидор має чотири лапи.

Л і т н і й Д о б р о д і й. А звідки ви знаєте?

Л о г і к. Це гіпотеза.

Л і т н і й Д о б р о д і й (до Логіка). Ага! Гіпотеза! [...]

Л о г і к (до Літнього Добродія). У Фріко теж чотири лапи. Скільки лап у Фріко та Ізидора?

Л і т н і й Д о б р о д і й (до Логіка). Разом чи окремо? [...]

Л о г і к (до Літнього Добродія). Разом чи окремо - це залежно від обставин. [...]

Л і т н і й Д о б р о д і й (до Логіка, після важких роздумів). Вісім, так, вісім лап.

Л о г і к. Логіка привчає рахувати подумки.

Л і т н і й Д о б р о д і й. Так, різнобічна наука! [...]

Л о г і к (до Літнього Добродія). Я позбавлю наших котів двох лап. Скільки зостанеться лап у кожного?

Л і т н і й Д о б р о д і й. Це важко. [...]

Л о г і к (до Літнього Добродія). Навпаки, дуже легко.

Л і т н і й Д о б р о д і й (до Логіка). Може, вам воно легко, та мені аж ніяк. [...]

Л о г і к (до Літнього Добродія). Візьміть папірця, порахуйте. Двох котів позбавити шести лап. Скільки зостанеться лап у кожного?

Л і т н і й Д о б р о д і й. Зачекайте... (Витягає з кишені папірця й рахує). [...]

Л і т н і й Д о б р о д і й (до Логіка). Тут може бути кілька розв'язків.

Л о г і к (до Літнього Добродія). Кажіть. [...]

Л і т н і й Д о б р о д і й (до Логіка). Перше припущення: в одного кота може бути чотири, а в другого - дві лапи. [...]

Л о г і к. У вас є здібності, досить тільки скористатися ними.

Л і т н і й Д о б р о д і й. В мене часу нема зовсім. Я урядовець.

Л о г і к (до Літнього Добродія). Щоб учитися, завжди найдеться час. [...]

Л і т н і й Д о б р о д і й (до Логіка). Це вже трохи запізно для мене.

Л о г і к (до Літнього Добродія). Запізно ніколи не буває. [...]

Л о г і к (до Літнього Добродія). Ну, а інші розв'язки? Візьміться тільки добре... [...]

Л і т н і й Д о б р о д і й (до Логіка). В одного кота може бути п'ять лап... [...] А в другого одна. Але чи будуть вони тоді котами?

Л о г і к (до Літнього Добродія). Чом би ні? [...]

Л і т н і й Д о б р о д і й (до Логіка). Якщо відкинути від восьми лап дві, то двоє котів... [...] В кота може бути й шість лап...[...] А другий кіт узагалі без лап. [...]

Л о г і к (до Літнього Добродія). В такому разі один кіт був би привілейований. [...]

Л і т н і й Д о б р о д і й. А той, що без лап буде декласованим елементом? [...]

Л о г і к. Тут нема справедливості. Отже, це вже не логіка. [...]

Л і т н і й Д о б р о д і й (до Логіка). Не логіка? [...]

Л о г і к (до Літнього Добродія). Бо справедливість - це логіка. [...]

Л і т н і й Д о б р о д і й (до Логіка). Справедливість - іще одна прикмета логіки. [...]

Л о г і к (до Літнього Добродія). Ваш розум прояснюється! [...]

Л і т н і й Д о б р о д і й (до Логіка). З іншого боку, зовсім безлапий кіт... [...]...не зміг би бігати досить прудко, щоб ловити мишей. [...]

Л о г і к (до Літнього Добродія). Ну, з логіки у вас уже успіхи! [...]

Л о г і к (до Літнього Добродія). Навіть безлапий кіт повинен ловити мишей. Натура в нього така. [...] (Ежен Йонеско. Носороги // Французька п'єса ХХ століття. Театральний авнгард. - К.: „Основи”, 1993. - с.448-452).

32. Охарактеризуйте полісилогізм, його структурну будову. Наведіть приклади прогресивних і регресивних полісилогізмів.

33. Прокоментуйте (спробуйте повністю відтворити міркування Холмса).

- Отже, Ватсоне, - промовив він зненацька, - ви не збираєтесь вкладати свої заощадження в південноафриканські цінні папери? [...]

- Як, чорт забирай, ви про це довідались? - запитав я. [...]

- Не так уже й важко побудувати низку виводів, в якій кожний наступний просто випливає з попереднього. Якщо після цього вилучити усі середні ланки і повідомити слухачу лише першу і останню ланки, вони справлять приголомшуюче, хоча і хибне враження. Після того як я помітив западинку між великим і вказівним пальцями вашої лівої руки, мені було зовсім неважко виснувати, що ви не збираєтесь вкладати свій невеликий капітал в золоті розсипи.

- Але я не бачу жодного зв'язку між цими двома обставинами!

- Охоче вірю. Проте я вам за декілька хвилин доведу що такий зв'язок існує. Ось випущені ланки цього найпростішого ланцюга: по-перше, коли вчора увечері ми повернулись із клубу, западинка між вказівним і великим пальцями вашої лівої руки була забруднена крейдою; по-друге, кожного разу, коли ви граєте на більярді, ви натираєте цю западинку крейдою, аби кий не ковзав у вашій руці; по-третє, ви граєте на більярді лише із Серстоном; по-четверте, місяць тому ви мені сказали, що Серстон запропонував вам придбати спільно із ним південноафриканські цінні папери, які надійдуть до продажу через місяць; п'яте, ваша чекова книжка замкнена у ящику мого письмового столу, і ви не попросили у мене ключа; шосте - ви не збираєтесь вкладати свої гроші в південноафриканські папери.

- Як просто! - вигукнув я.

- Звичайно, - сказав він, трохи уражений, - будь-яка задача виявляється дуже простою після того, як вам її розтлумачать. (Артур Конан Дойль. Записки о Шерлоке Холмсе. - К.: „Молодь”, 1957. - с.286-287).

34. В чому полягає специфічність ентимеми? Чому ентимему інколи називають риторичним силогізмом або „силогізмом із імовірного”? Наведіть приклади ентимем.

35. Створіть усі можливі ентимеми із силогізмів, що наведені у вправі (25).

36. Встановіть, висновок чи засновок (більший або менший) пропущено в запропонованих ентимемах:

(а) „Ця задача є нерозв'язуваною; тому її не вирішив жодний математик”;

(б) „Деякі книги - шкідливі, бо усе непотрібне – шкідливе”;

(в) „Усі англійці п'ють чай з молоком, але жоден француз не є англійцем”;

(г) „Жоден підручник цього автора не користується популярністю. Тому цей підручник не є підручником цього автора”;

(д) „Якщо він не вкрав цю річ, то для чого він її заховав?”.

37. Чи є правильними запропоновані ентимеми?

(а) „Олег готується до іспитів. Отже, він буде їх складати”;

(б) „Цей студент склав усі іспити, бо він отримує стипендію”;

(в) „Кожна людина бажає доброчесності, бо кожна людина бажає щастя”;

(г) „Шахрайство - злочин, позаяк воно підпадає під карну

відповідальність”;

(д) „Більшість викладачів університету навчались в університеті. Отже, і

Н. навчався в університеті”;

(е) „Раб - людина, тому його не можна тримати в неволі”;

(є) „Деякі студенти не люблять курсу „Логіка”, бо від цього курсу у них болить голова”;

(ж) „Справжній філософ не залежить від примх долі, бо він знаходить своє щастя у

розумовому і моральному вдосконаленні”.

38. Проаналізуйте міркування:

(а) „Певно якась маленька домішка польської крові текла в жилах викладача латинської мови в Охтирській гімназії Олександра Едуардовича Олександровича. Про це свідчило тільки те, що ніхто в Охтирці не вмів так віртуозно танцювати мазурку, як він” (Антоненко-Давидович Б.Д. Смерть. Сибірські новели. Завищені оцінки. - К.: „Радянський письменник", 1989. - с.333).

(б) „Немає жінки, яка б не припускала, що в неї сховані таланти актриси. Вер була жінка, - отже, вона уявляла себе – принаймні деякий час – акторкою” (Домонтович В. Доктор Серафікус. Без грунту. Романи. – К.: Критика, 1999. – с.66).

49. Охарактеризуйте сутність, будову прогресивних і регресивних соритів. Наведіть відповідні приклади.

40. Проаналізуйте міркування (встановіть його вид і правильність):

(а)

Віруюча людина шанує Бога;

Той, хто шанує Бога, шанує його заповіти;

Один серед заповітів - милосердя до ближнього;

Милосердя запобігає злочинам;

Запобігання злочинам слугує інтересам держави;

Отже, віруюча людина служить інтересам держави.

(б)

Це міркування є барбаризмом;

Жодний барбаризм не є хелоптичним;

Усе, що є правильним є хелоптичним;

Отже, це міркування не є правильним.

41. Охарактеризуйте сутність і будову епіхейрем. Наведіть відповідні приклади.

*****