Анализ корреляционной зависимости (КА) переменных позволяет установить наличие связи между анализируемыми переменными, оценить ее тесноту и определить направление (прямая или обратная связь). Кроме того, в ходе КА происходит отбор существенных факторов, включаемых в уравнение регрессии.
В ходе множественного КА рассчитываются следующие характеристики:
- парные коэффициенты корреляции 
– оценки тесноты линейной корреляционной связи между всеми парами анализируемых признаков с учетом их взаимного влияния и взаимодействия. Совокупность парных коэффициентов корреляции, относящихся ко всем исследуемым признакам, может быть представлена в виде корреляционной матрицы R, которая рассчитывается по формуле
, (2.1)
где 
– матрица стандартизованных значений исходных переменных. Ее элементы рассчитываются по формуле
.
На главной диагонали матрицы R стоят единицы, т.е. дисперсии стандартизованных переменных, другие элементы — парные коэффициенты корреляции ;
- частные коэффициенты корреляции 
, характеризующие тесноту линейной корреляционной связи между парой анализируемых признаков (
и 
)без учета влияния на эту пару других переменных (
, 
, и т.д.). Эти коэффициенты характеризуют так называемую чистую корреляцию. В матричном виде формулу для расчета частных коэффициентов корреляции можно записать следующим образом:
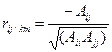, (2.2)
где 
, 
, 
– алгебраические дополнения соответствующих элементов матрицы парных корреляций R.
Знак частному коэффициенту корреляции присваивается такой же, как и у парного коэффициента корреляции;
-множественный коэффициент корреляции 
характеризует степень тесноты связи между результативным признаком (откликом) 
и всеми факторными признаками (предикторами – 
);
-множественный коэффициент детерминации 
характеризует долю дисперсии результативной переменной, обусловленную влиянием факторных переменных, участвующих в анализе. На основе корреляционной матрицы R множественный коэффициент корреляции и множественный коэффициент детерминации могут быть исчислены следующим образом:
; 
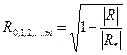, (2.3)
где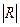 
– определитель матрицы парных корреляций, 
– определитель матрицы парных корреляций, полученной после вычеркивания строки и столбца, представляющих связи зависимой переменной ().
Пример 1. По пяти промышленным предприятиям имеются следующие данные о фондовооруженности труда рабочих (
), уровне производительности труда (
), удельном весе потерь от брака (
) (таблица 2.1).
Таблица 2.1
| Номер предприятия | Фондовооруженность труда рабочего, тыс. ден. ед. | Месячная производительность труда рабочего, тыс. ден. ед. | Удельный вес потерь от брака, % |
|
|
|
| |
| 3,9 | 7,0 | 2,4 | |
| 1,1 | 11,1 | 5,9 | |
| 1,8 | 10,2 | 6,2 | |
| 6,0 | 12,0 | 6,0 | |
| 5,4 | 10,0 | 11,0 | |
| 
| 
| |
| 
| 
|
Определить:
1) матрицы парных и частных коэффициентов корреляции;
2) множественный коэффициент детерминации и множественный коэффициент корреляции при условии, что – зависимая переменная;
3) матрицу ковариаций.
Решение.
1 Парные коэффициенты корреляции рассчитываются следующим образом:
;
;
.
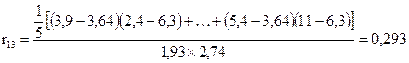Матрица парных коэффициентов корреляции имеет вид
.
2 Частные коэффициенты корреляции рассчитываются по формуле
; 
; 
;
;
;
.
Матрица частных коэффициентов корреляции (
) будет иметь вид
.
3 Множественный коэффициент корреляции определяется по формуле
; 
.
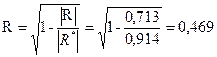4. Элементы ковариационной матрицы 
определяются по формуле
.
В многомерном статистическом анализе ковариации принято иногда обозначать как 
(по аналогии с дисперсиями).
Рассчитаем последовательно все элементы ковариационной матрицы:
;
;
; 
;
; 
.
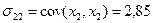Матрица ковариаций будет иметь следующий вид:
.
На основании матрицы ковариаций можно сравнить вариацию признаков в исследуемой статистической совокупности. Для этого рассчитаем коэффициенты ковариации по каждой переменной:
; 
;
; 
.
Как показывают расчеты, исследуемая совокупность наиболее однородна по второй переменной – месячная производительность труда, а наименее однородна по переменной – фондовооруженность труда рабочего.
Используя элементы ковариационной матрицы, можно также проверить правильность расчета парных линейных коэффициентов корреляции
.
Например, коэффициент корреляции между переменными 
и 
будет равен
,
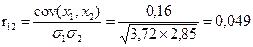а в корреляционной матрице он равен 0,048, т.е. имеется небольшое расхождение за счет округлений.
