Операторомв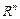 
(преобразованием пространства 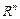) называется закон, по которому каждому вектору 
ставится в соответствие единственный вектор 
, и пишут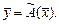 
Оператор 
называется линейным, если для любых векторов 
и действительных чисел 
выполнено условие: 
.
Если 
- базис 
, то матрицей линейного оператора в базисе 
называется квадратная матрица 
порядка 
, столбцами которой являются столбцы координат векторов 
. Каноническим базисом называется базис 
, где 
, 
, 
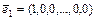-единичные векторы. Между линейными операторами, действующими в 
и квадратными матрицами порядка , существует взаимно однозначное соответствие, что позволяет оператор 
представлять в матричном виде 
, где 
- матрицы-столбцы координат векторов 
, - матрица оператора в базисе .
Для линейных операторов вводятся операции: 1) сложение операторов: 
; 2 ) умножение оператора на число: 
; 3) умножение операторов: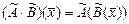 
. Обратным к оператору называется оператор 
такой, что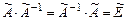 
, где 
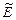- единичный(тождественный) оператор, реализующий отображение 
. Обратный оператор 
существует только для невырожденных операторов (операторов, матрица которых является невырожденной). Все, рассмотренные выше, действия над линейными операторами выполняют, выполняя аналогичные действия над их матрицами.
Пусть число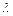 
и вектор , 
, таковы, что выполняются равенства: 
или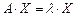 
. Тогда число 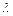называется собственным числом линейного оператора (матрицы ), а вектор 
- собственным вектором оператора (матрицы), соответствующим собственному числу 
. Равенство 
может быть записано и в виде 
, где 
- единичная матрица порядка , 
- матрица-столбец координат собственного вектора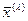 
, соответствующего собственному числу , 
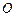- нулевая матрица-столбец. Характеристическим уравнением оператора (матрицы 
) называется уравнение: 
.
Множество собственных чисел оператора (матрицы) совпадает с множеством корней его характеристического уравнения: 
, а множество собственных векторов, отвечающих собственному числу 
, совпадает с множеством ненулевых решений матричного уравнения: 
.
Если квадратная матрица порядка 
имеет собственные числа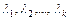 
кратности 
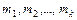, где 
, то она приводима к диагональному виду 
тогда и только тогда, когда выполнены условия: 
(
). Если нарушается хотя бы одно из условий, то матрица к диагональному виду неприводима. В диагональной матрице на главной диагонали стоят собственные числа матрицы .
В задачах 1.134-1.138 установить, какие из заданных отображений пространства арифметических векторов 
в себя являются линейными операторами, и выписать их матрицы в каноническом базисе.
1.134 
. 1.135 
.
1.136 
. 1.137 
.
В задачах 1.139-1.143 в пространстве заданы линейные операторы 
и 
. Найти матрицу линейного оператора 
, где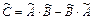 
и его явный вид в каноническом базисе .
1.139 
, 
.
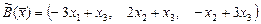1.140 
, 
.
1.141 
, 
.
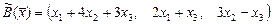1.142,.
