Практическое занятие.
Тема. Скалярное произведение геометрических векторов. Проекция вектора на вектор. Применение скалярного произведения для решения геометрических задач.
Тема. Векторное и смешанное произведения векторов, их применение для решения геометрических задач.
2.53 Найти скалярное произведение коллинеарных и противоположно направленных векторов 
, если 
2.54 Вычислить: а) 
; б) 
, если 
, 
, 
.
2.55 Найти модуль вектора 
где 
единичные векторы, угол между которыми равен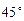 
.
2.56 Определить, при каком значении 
векторы 
и 
будут перпендикулярны, если 
2.57 Какой угол образуют единичные векторы 
и 
, если известно, что векторы 
и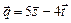 
взаимно перпендикулярны?
2.58 Вычислить длину диагоналей параллелограмма, построенного на векторах 
если известно, что 
.
2.59 Определить угол между векторами 
и 
, если известно, что 
, 
, 
.
2.60 Вычислить 
.
2.61 Даны векторы 
и 
. Вычислить: а) 
; б)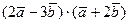 
;
В); г); д); е); ж).
Даны три вектора: Вычислить: а); б).
2.63 Даны векторы: 
. При каком значении векторы и будут перпендикулярны.
2.64 Найти угол между диагоналями параллелограмма, построенного на векторах 
2.65 Даны точки 
.На оси абсцисс найти такую точку М, чтобы 
2.66 Даны три вектора: 
Найти вектор 
, удовлетворяющий одновременно уравнениям: 
, 
, 
.
2.67 Найти координаты вектора , коллинеарного вектору 
и удовлетворяющего условию 
.
2.71 Вычислить, если 
: а) 
; б) 
.
2.72 Упростить выражения: а) 
б) 
;
в) 
; г) 
.
2.73 Вычислить площадь параллелограмма, построенного на векторах 
единичные векторы, величина угла между которыми равна 60°.
2.74 Вычислить площадь параллелограмма, диагоналями которого служат векторы 
и 
, где 
- единичные векторы и 
2.75 Найти координаты вектора 
, если:
a) 
б) 
2.77 Определить, при каких значениях 
и 
вектор 
будет коллинеарен вектору 
если
А); б).
2.78 Найти вектор 
, если 
.
2.79 Вычислить площадь треугольника с вершинами в точках 
, 
, 
.
2.80 В треугольнике с вершинами в точках 
найти высоту 
2.81 Даны два вектора: 
Найти вектор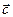 
единичной длины, перпендикулярный к векторам 
, 
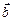и направленный так, чтобы упорядоченная тройка векторов 
имела положительную ориентацию.
2.82 Вектор 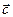, перпендикулярный оси Oz и вектору 
образует острый угол с осью Ox. Зная, что 
, найти его координаты.
2.83 Найти координаты вектора 
, если известно, что он перпендикулярен векторам 
и 
, образует с ортом 
тупой угол и 
.
2.84. Найти координаты вектора , если он перпендикулярен векторам 
и 
, а также удовлетворяет условию 
.
2.88 Векторы 
образуют правую тройку, взаимно перпендикулярны и 
Вычислить 
.
2.89 Векторы 
образуют левую тройку. Найти , если 
2.90 Определить ориентацию тройки векторов 
если:
А); б).
Вычислить произведения, если:а) б).
2.93 Проверить, компланарны ли векторы a) 
;
б)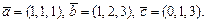 
2.94 При каком 
векторы будут компланарны? а) 
б) 
2.95 Установить, образуют ли векторы 
базис в множестве всех векторов, если
a) 
; б) 
2.96 Проверить лежат ли точки в одной плоскости
а) 
, B (1,2,1), C (2,3,0), 
; б) A (7,0,3), 
, 
, 
.
2.97 Вычислить объём тетраэдра 
, если 
, 
, 
.
2.98 Объем тетраэдра равен 5, три его вершины находятся в точках 
, B (3,0,1), 
. Найти координаты четвертой вершины D, если известно, что она лежит на оси ординат.
2.99 В тетраэдре 
вершины которого расположены в точках 
, 
, 
, 
, найти длину высоты 
.
Ответы: 2.53 
. 2.54 
. 2.55 
. 2.56 
. 2.57 
. 2.58 15 и 
. 2.59 
2.60 
. 2.61a) 
б) 
в) 
г) 
д) 
е) 
ж) 
. 2.62 а) 15; б) 
. 2.63 
. 2.64 
2.65 
. 2.66 
. 2.67 
. 2.68 4. 2.69 
. 2.70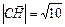 
. 2.71а) 
; б) . 2.72 а) 
; б) 
; в) 
; г) 
. 2.73 
2.74 
. 2.75 а) 
; б) 
. 2.76 а) 
; б) 
. 2.77 а) 
; б) 
. 2.78 
. 2.79 
. 2.80 
. 2.81 
. 2.82 
. 2.83 
2.84 
2.85 
2.86 
2.87 
2.88 24. 2.89 
2.90 а) левая; б) правая. 2.92 а)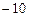 
; б) 
2.93 а) компланарны; б) некомпланарны. 2.94 а) 
; б) 
. 2.95 а) нет; б) да. 2.96 а) нет; б) да. 2.97 
2.98 
, 
2.99 
.
