Система линейных алгебраических уравнений вида
(6.5)
называется однородной системой линейных алгебраических уравнений.
Очевидно, что однородная система всегда совместна, так как для нее всегда существует тривиальное решение 
. Кроме того, она может иметь и нулевое решение.
1. Однородная система имеет ненулевое решение тогда и только тогда, когда ранг матрицы системы меньше числа неизвестных, т.е. 
, где 
, А – матрица системы.
2. Однородная система, в которой число уравнений равно числу неизвестных, имеет ненулевое решение тогда и только тогда, когда ее определитель 
равен нулю.
Пример. Решить систему 
.
Решение. Система однородная, следовательно, она имеет единственное решение или множество решений. Для выяснения этого найдем ранг основной матрицы (он всегда равен рангу расширенной) и сравним его с числом неизвестных.
Ранг матрицы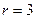 
и равен числу неизвестных, система имеет единственное нулевое решение.
Пример. Решить систему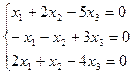 
.
Решение:
Система однородная, всегда совместная. Исследуем, имеет ли она ненулевое решение. Преобразуем основную матрицу системы:
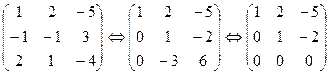
Так как 
, а число неизвестных равно трем, то система имеет множество решений, среди которых будут и ненулевые. Восстановим систему по последней матрице:
Из последнего уравнения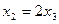 
, из первого находим 
, где 
- любое число.
Задачи для практических занятий
и самостоятельной работы
Решить системы линейных алгебраических уравнений, используя формулы Крамера:
1. 
2. 
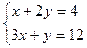
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
Решить системы линейных алгебраических уравнений матричным методом:
11. 
12. 
13. 
14.
Решить системы линейных алгебраических уравнений методом Гаусса:
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
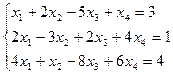
23. 
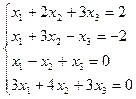
24. 
25. 
26. 
27. 
28. 
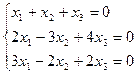
29. 
30. 
Ответы
1. 
, 
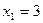2. 
, 
3. 
, 
, 
4. 
, 
, 
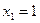5. система несовместна
6. 
, 
, 
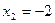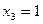
7. 
, , 
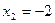8. 
, 
, 
9. система несовместна
10. 
, , 
, 
11. , , 
12. , ,
13. , , 
14. , ,
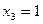
15. , 
,
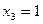
16. , , 
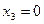
17. система несовместна
18. 
, 
, 
- любое число
19. , 
, 
20. , ,
21. 
, 
, - любое число
22. система несовместна
23. , ,
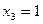
24. , ,
25. система несовместна
26. 
, 
, , 
- любые числа
27. 
, 
, , - любые числа
28. 
29. 
, 
, 
, - любое число
30. 
Литература
1. Бугров Я.С., Никольский С.М. Элементы высшей линейной алгебры и аналитической геометрии. – М.: Наука, 1980 г.
2. Головина Л.И. Линейная алгебра и некоторые ее приложения. – М.: Наука, 1979 г.
3. Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. – М.: Наука, 1977 г.
Учебное издание
Ивина Н.А.
Методические указания к практическим занятиям
РГТК, 2002 г. – 44 с.
Подписано в печать 06.09.2002 г. Формат А5
Бумага для офсетной печати
Отпечатано на ризографе.
Тираж 200 экземпляров. Заказ № 73
Рязанский государственный технологический колледж
390035 г. Рязань, пр. Гоголя, 6.
Лицензия Б 794164 № 0001 от 18.03.99
 |
