Пример 1. Решить уравнение 
Решение. Выразим из уравнения 
Получили однородное уравнение. Делаем замену 
– уравнение с разделяющимися переменными. Решаем его: 
Возвращаясь к старой переменной у, получаем: 
Ответ:
Пример 2. Найти решение задачи Коши 
Решение. Разделим обе части уравнения на x: 
Получили линейное уравнение.
Решаем уравнение: 
Разделяем переменные: 
Интегрируем обе части: 
Пользуясь свойствами логарифма, получаем 
(Мы ввели новую константу С 1, связанную со старой следующим образом: С = ln C 1). Считая С 1 функцией от x, подставляем в полученное линейное уравнение 
и 
Отсюда находим 
C 1 = sin x + B, где B – константа.
Используя начальные условия, найдём константу В. 
Ответ: 
Пример 3. Найти частное решение дифференциального уравнения второго порядка, удовлетворяющее указанным начальным условиям: 
, 
Решение. Дано ЛНДУ II порядка с постоянными коэффициентами и специальной правой частью. Решение уравнения ищем в виде
а) Найдем 
: 
Его характеристическое уравнение 
; 
Значит 
б)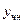 
ищем, используя метод неопределённых коэффициентов 
, 
, 
.
Подставив 
, в исходное уравнение, получаем
Чтобы найти частное решение этого уравнения, удовлетворяющее заданным начальным условиям, продифференцируем 
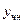
Подставим в и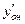 
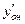вместо x = 0, = 0, = 1.
Подставим найденные 
и 
в : 
.
Ответ: .
Пример 4. Дан степенной ряд 
. Написать первые четыре члена ряда, найти интервал сходимости ряда и исследовать его сходимость на концах интервала.
Решение: 
Найдём радиус сходимости:
Интервал сходимости: 
Рассмотрим концы интервала:
при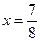 
получим ряд 
, следовательно (по признаку сравнения) ряд расходится.
при 
получим ряд 
, это знакочередующийся ряд. Проверим выполнение условий признака Лейбница:
1) 
2) 
т.е. 
Условия выполнены, значит ряд сходится.
Ответ: Ряд сходится при 
Пример 5. Найти четыре члена разложения функции 
в ряд Маклорена.
Решение. Используем известное разложение
область сходимости –1 < x £ 1.
Итак:
область сходимости 
Пример 6. В группе 18 студентов из которых, из которых 8 имеют задолженность по математическому анализу. Какова вероятность того, что из 10 произвольно выбранных студентов 3 человек имеют задолженность?
Решение. Такие задачи описываются общей схемой. Имеется совокупность из N 1 элементов первого вида и N 2 элементов второго вида. Какова вероятность того, что при выборе совокупности из k элементов она состоит из k 1 элементов первого вида и k 2 элементов второго вида, где k = k 1 + k 2, k 1 £ N 1, k 2 £ N 2.
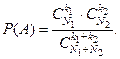
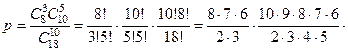
Пример 7. Предполагаем, что рост призывника – нормально распределенная случайная величина Х, с математическим ожиданием а и средним квадратическим отклонением s. В специальную команду нужно отобрать призывников ростом от х1 до х2 сантиметров. Определить: а) вероятность того, что наудачу взятый призывник попадёт в специальную команду; б) вероятность того, что абсолютная величина отклонения Х–а окажется меньше d; в) по правилу трех сигм найти наибольшую и наименьшую границы предполагаемого роста призывника.
| а | s | х1 | х2 | d |
Решение. а) Для нормально распределённой случайной величины
б) 
с) По правилу трёх сигм наименьшая граница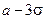 
, наибольшая 
. Таким образом, 
.
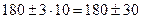Наименьшая граница 150 см, наибольшая 210 см.
Пример 8. Задан закон распределения дискретной случайной величины. Найти:
1) значение параметра а;
2) математическое ожидание М(Х);
3) дисперсию D(Х).
Построить многоугольник распределения.
| Х | |||||
| р | 0,2 | 0,1 | 0,3 | 0,2 | а |
Решение.
1) 
2) 
3) 
4) многоугольник распределения:
Пример 9. Случайная величина Х задана функцией распределения.
Требуется:
1) найти функцию плотности вероятности f(x);
2) найти математическое ожидание и дисперсию случайной величины Х;
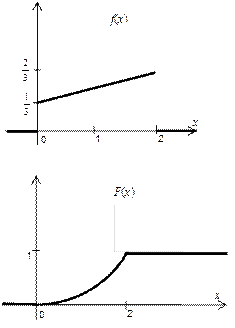
3) построить графики функций F(x) и f(x).
Решение:
1) 
, 
2) Найдём М (X) по формуле 
.
.
Дисперсию вычисляем по формуле
.
3) Построим графики функций 
и 
.
Пример 10. Закон распределения двумерной дискретной случайной величины (Х, Y) задан таблицей.
| Y | ||||
| X | ||||
| 1/18 | 1/12 | 1/36 | ||
| 1/9 | 1/6 | 1/18 | ||
| 1/6 | 1/4 | 1/12 |
Найти:
1) частные законы распределения случайных величин Х и Y;
2) математические ожидания М (Х) и М (Y);
3) дисперсии D (Х) и D (Y);
4) корреляционный момент Cxy;
5) коэффициент корреляции rxy;
6) условный закон распределения случайной величины Х при условии, что случайная величина Y принимает своё наименьшее значение.
Решение:
1) частный закон распределения случайной величины Х:
проверка: 
верно.
| хi | |||
| pi | 1/6 | 1/3 | 1/2 |
частный закон распределения случайной величины Y:
проверка: 
верно.
| yi | |||
| pi | 1/3 | 1/2 | 1/6 |
2) Математические ожидания случайных величин X и Y:
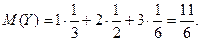
3) Дисперсии D (Х) и D (Y):
,
.
4) Корреляционный момент Cxy:
.
5) коэффициент корреляции 
где 
– среднеквадратические отклонения.
Так как у нас 
то и 
6) условный закон распределения случайной величины Х при условии, что случайная величина Y принимает своё наименьшее значение.
Наименьшее значение 
при этом 
По формуле 
находим:
Условный закон распределения
| |||
| pi | 1/6 | 1/3 | 1/2 |
Вопросы к экзамену
1. Дифференциальные уравнения первого порядка: с разделяющимися переменными, однородные и приводящиеся к ним, линейные, Бернулли.
2. Уравнения, допускающие понижение порядка.
3. Определитель Вронского. Свойства линейных однородных уравнений.
4. Структура общего решения линейного однородного уравнения второго порядка с постоянными коэффициентами.
5. Неоднородное линейное уравнение второго порядка. Метод вариации произвольных постоянных.
6. Частное решение неоднородного линейного уравнения второго порядка с постоянными коэффициентами.
- Ряды. Свойства рядов. Необходимый признак сходимости.
- Расходимость гармонического ряда.
- Признаки Даламбера, Коши, сравнения, интегральный признак Коши.
- Признак Лейбница.
- Свойства абсолютно сходящихся и условно сходящихся рядов.
- Интегрирование и дифференцирование равномерно сходящихся рядов.
- Классическое и геометрическое определения вероятности. Свойство вероятности.
- Теоремы сложения и умножения.
- Формула полной вероятности. Вероятность гипотез. Формулы Байеса
- Повторные независимые испытания. Формула Бернулли.
- Теорема Муавра - Лапласа; интегральная теорема Лапласа
- Операции над СВ.
- Свойства М(X), D(X).Формулы для вычисления D(X).
- Одинаково распределенные взаимнонезависимые СВ.
- Начальные и. центральные теоретические моменты.
- Биномиальное распределение, распределение Пуассона их числовые характеристики.
- Функция распределения, ее свойства.
- Плотность распределения вероятностей, ее свойства
- Числовые характеристики непрерывных СВ
- Равномерное, нормальное, показательное распределения, их числовые характеристики.
- Кривая Гаусса.
- Неравенство Чебышева, теорема Чебышева, теорема Бернулли.
