Контрольной работы
При выполнении контрольной работы студент должен руководствоваться следующими указаниями.
1. Работа должна выполняться в отдельной тетради (в клетку), на внешней обложке которой должны быть разборчиво написаны фамилия студента, его инициалы, полный шифр, номер контрольной работы, дата отсылки работы в институт.
2. Задачи следует располагать в порядке возрастания номеров. Перед решением каждой задачи надо полностью переписать её условие.
3. Решение задач следует излагать подробно, делая соответствующие ссылки на вопросы теории с указанием необходимых формул, теорем.
4. Решение задач геометрического содержания должно сопровождаться чертежами, выполненными аккуратно, с указанием осей координат и единиц масштаба. Объяснения к задачам должны соответствовать обозначениям, приведённым на чертежах.
5. На каждой странице тетради необходимо оставлять поля шириной 3-4 см для замечаний преподавателя.
6. Контрольная работа должна выполняться самостоятельно. Несамостоятельно выполненная работа лишает студента возможности проверить степень своей подготовленности по теме.
7. Если преподаватель установит несамостоятельное выполнение работы, то она не будет зачтена.
8. Получив прорецензированную работу (как зачтённую, так и незачтённую), студент должен исправить все отмеченные рецензентом ошибки и недочёты. В случае незачёта по работе студент обязан в кратчайший срок выполнить все требования рецензента и представить работу на повторное рецензирование, приложив при этом первоначально выполненную работу.
9. Студент выполняет тот вариант контрольной работы, который совпадает с последней цифрой его учебного шифра.
| № варианта | Номера задач контрольных работ по вариантам | |||||||||
| Контрольная работа №5 | Контрольная работа №6 | |||||||||
Контрольная работа №5
В задачах 1–10 найти общее решение (общий интеграл) дифференциальных уравнений первого порядка.
1.  2.
2. 
3. 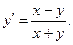 4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  20.
20. 
В задачах 11-20 найти решение задачи Коши.
11. 

12. 

13. 

14. 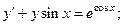

15. 

16. 

17. 
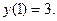
18. 

19. 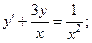

20. 

В задачах 21-30 найти общее решение дифференциального уравнения.
21.  22.
22. 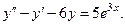 23.
23.  24.
24.  25.
25. 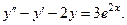 26.
26. 
27.  28.
28.  29.
29. 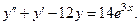 30.
30. 
В задачах 31-40 дан степенной ряд  Написать первые четыре члена ряда, найти интервал сходимости ряда и выяснить вопрос о сходимости ряда на концах интервала. Числа а, b и k даны.
Написать первые четыре члена ряда, найти интервал сходимости ряда и выяснить вопрос о сходимости ряда на концах интервала. Числа а, b и k даны.
31.  32.
32. 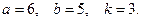
33.  34.
34. 
35.  36.
36. 
37.  38.
38. 
39.  40.
40. 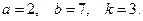
В задачах 41-50 найти четыре члена разложения функции в ряд Маклорена.
41. 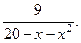 42.
42. 
43.  44.
44. 
45.  46.
46. 
47.  48.
48. 
49.  50.
50. 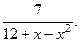
Контрольная работа №6
51. В коробке 15 луковиц гладиолусов, из которых 7 луковиц красных гладиолусов, 8 луковиц черных. Какова вероятность того, что из 10 наудачу выбранных луковиц 6 окажутся луковицами черных гладиолусов?
52. Из 12 луковиц, среди которых 5 луковиц красных тюльпанов и 7 желтых, наудачу выбирают 4. Какова вероятность того, что из них вырастут два красных и два желтых тюльпана?
53. В помете 2 рыжих щенка и 5 черных. Наудачу выбирают трех щенков. Какова вероятность того, что один из них рыжий?
54. Из 12 крыс 8 получили некоторую дозу облучения. Какова вероятность того, что из 6 наудачу выбранных крыс 4 облучены?
55. В популяции из 30 плодовых мушек 10 имеют красные глаза. Наудачу выбирают 5 мушек. Какова вероятность того, что одна из них имеет красные глаза?
56. В 15 пакетиках находится пыльца, собранная с 15 цветков гороха, из которых 5 красных, а остальные – белые. Наудачу выбирают 3 пакетика. Какова вероятность того, что в двух из них пыльца красных цветков?
57. Среди 12 цыплят 5 курочек. Какова вероятность того, что из выбранных наудачу 4 цыплят 2 курочки?
58. Из данных 20 мужчин 1 страдает дальтонизмом. Какова вероятность того, что при случайном выборе 10 мужчин из этих 20 один страдает дальтонизмом?
59. Из колоды в 36 карт выбирают 4 карты. Какова вероятность того, что 3 из них красные?
60. Из 15 вакцинированных мышей у 12 сформировался иммунитет. Какова вероятность того, что из 5 случайно выбранных из группы вакцинированных мышей 4 имеют иммунитет?
В задачах 61-70 Известно, что рост людей, проживающих в данной местности, есть случайная величина Х, распределенная по нормальному закону со средним значением а и средним квадратическим отклонением s. Найти: а) вероятность того, что наудачу выбранный человек имеет рост от х1 до х2 см; б) вероятность того, что абсолютная величина отклонения Х–а окажется меньше d; в) по правилу трех сигм найти наибольшую и наименьшую границы предполагаемого роста человека.
| Номер задачи | а | s | х1 | х2 | d |
В задачах 71-80 задан закон распределения дискретной случайной величины.
Найти:
1) значение параметра а;
2) математическое ожидание М(Х);
3) дисперсию D(Х).
Построить многоугольник распределения.
71.
| Х | |||||
| р | 0,3 | 0,2 | 0,3 | 0,1 | а |
72.
| Х | |||||
| а | 0,2 | 0,4 | 0,3 | р | 0,1 |
73.
| Х | |||||
| р | 0,2 | 0,1 | 0,5 | 0,1 | а |
74.
| Х | |||||
| р | 0,1 | 0,4 | а | 0,3 | 0,1 |
75.
| Х | |||||
| р | 0,1 | 0,2 | 0,5 | 0,1 | а |
76.
| Х | |||||
| р | 0,1 | 0,4 | 0,2 | 0,1 | а |
77.
| Х | |||||
| р | 0,2 | 0,4 | а | 0,3 | 0,1 |
78.
| Х | |||||
| р | 0,2 | 0,3 | 0,1 | 0,3 | а |
79.
| Х | |||||
| р | 0,2 | 0,3 | а | 0,3 | 0,1 |
80.
| Х | |||||
| р | 0,3 | 0,3 | а | 0,1 | 0,2 |
В задачах 81-90 случайная величина Х задана функцией распределения. Требуется:
1) найти функцию плотности вероятности f(x);
2) найти математическое ожидание и дисперсию случайной величины Х;
3) построить графики функций F(x) и f(x).
81. 
82. 
83. 
84. 
85. 
86. 
87. 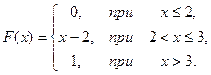
88. 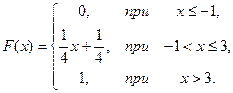
89. 
90. 
В задачах 91–100 закон распределения двумерной дискретной случайной величины (Х, Y) задан таблицей. Найти:
1) частные законы распределения случайных величин Х и Y;
2) математические ожидания М (Х) и М (Y);
3) дисперсии D (Х) и D (Y);
4) корреляционный момент Cxy;
5) коэффициент корреляции rxy;
6) условный закон распределения случайной величины Х при условии, что случайная величина Y принимает своё наименьшее значение.
| 91. | 92. | |||||||
| Х Y | Х Y | |||||||
| –1 | 0,1 | 0,1 | –1 | 0,1 | 0,1 | 0,1 | ||
| 0,2 | 0,2 | 0,1 | 0,2 | 0,2 | 0,2 | |||
| 0,2 | 0,1 | 0,1 |
| 93. | 94. | |||||||
| Х Y | –3 | Х Y | –3 | –2 | ||||
| –1 | 0,1 | 0,2 | 0,1 | 0,2 | 0,2 | |||
| 0,1 | 0,2 | 0,1 | 0,1 | 0,1 | 0,1 | |||
| 0,1 | 0,1 | 0,1 | 0,2 |
| 95. | 96. | |||||||
| Х Y | Х Y | –3 | ||||||
| –2 | 0,1 | 0,1 | 0,1 | 0,2 | 0,1 | |||
| 0,2 | 0,2 | 0,1 | 0,1 | 0,2 | 0,1 | |||
| 0,1 | 0,1 | 0,1 | 0,1 | 0,1 |
| 97. | 98. | |||||||
| Х Y | –3 | Х Y | ||||||
| –1 | 0,1 | 0,1 | 0,1 | –2 | 0,2 | 0,1 | ||
| 0,1 | 0,2 | 0, | –1 | 0,2 | 0,1 | 0,1 | ||
| 0,2 | 0,2 | 0,1 | 0,1 | 0,1 |
| 99. | 100. | |||||||
| Х Y | –1 | Х Y | ||||||
| –1 | 0,1 | 0,1 | 0,1 | 0,2 | 0,1 | 0,1 | ||
| 0,1 | 0,2 | 0,1 | 0,1 | 0,2 | 0,1 | |||
| 0,1 | 0,1 | 0,1 | 0,1 | 0,1 |






