Применяется для определения тока в одной ветви электрической схемы. Считаем, что эта ветвь с сопротивлением 
присоединяется к остальной части цепи (активному двухполюснику) в точках a и b (рис. 2).
Рис.2 - К методу эквивалентного генератора
Заменяют активный двухполюсник эквивалентным генератором с э.д.с. 
и внутренним сопротивлением 
Для этого:
1. Определяется как напряжение холостого хода 
между a и b (при отсоединенном 
).
2.Определяется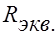 
как входное сопротивление эквивалентного генератора между a и b при замене входящих в эквивалентный генератор источниках питания их внутренними сопротивлениями.
3.Рассчитывается ток через по формуле:
Метод узлового напряжения
Является частным случаем предыдущего метода и применяется для расчета токов в ветвях с двумя узлами.
1. Выбирается направление тока в ветвях, одинаковое для всех ветвей
(например, от узла b к a).
2. Определяется узловое напряжение:
,
где 
- проводимость к-той ветви;
- э.д.с. к-той ветви (
, если направлена по току в к-той ветви)
3. Определяются токи в ветвях:
Потенциальная диаграмма
Для построения потенциальной диаграммы:
1. выбирают произвольно направление обхода заданного контура.
2. принимают потенциал одной из точек контура равным нулю.
3. рассчитывают потенциалы 
всех других точек через потенциал предыдущей точки по формулам:
- для участков, содержащих резисторы (
>0, если 
совпадает с обходом контура);
- для участков, содержащих источники э.д.с. (
>0, если совпадает с обходом контура).
Строят график 
, откладывая по оси абсцисс сопротивления участков контура (внутренние сопротивления источников э.д.с. принимаются равными нулю), а по оси ординат – потенциалы точек контура между каждой парой элементов.
Баланс мощности электрической цепи
Правильность расчета токов в схеме проверяется составлением уравнения баланса мощностей:
,
где 
- мощность источника. (
, если совпадает по направлению с );
- мощность приемника.
Пример расчета
Рис. 3 - Исходная схема
Дано: E1 = 10В, E2 = 20 B, E3 = 30 B,
R1 = R2 = R3 = 2 Oм,
R4 = R5 = R6 = 1 Oм
Задание:
1. Преобразовать звезду R1 R2 R4 (рис.3) в треугольник.
2. Определить токи в ветвях исходной схемы методами:
- непосредственного применения законов Кирхгофа;
- методом наложения;
- методом контурных токов.
3. Определить токи в ветвях преобразованной схемы методом узловых потенциалов.
4. Определить ток через R3 методом эквивалентного генератора.
5. Составить баланс мощностей для преобразованной схемы.
6. Построить потенциальную диаграмму для контура АВЕДСА исходной схемы.
Решение:
1.Преобразуем звезду R1 R2 R4 в треугольник.
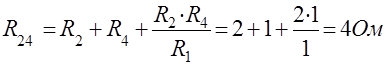
Рис.4 - Преобразованная схема
Преобразованная схема имеет вид, показанный на рис.4.
