1.Определяется число узлов схемы n и число ветвейв схеме m.
2.Произвольно выбирается направление токов во всех ветвях и направление обхода (m-n+1) контуров.
3.Составляется система из m уравнений, где (n-1) уравнений составляются по I закону Кирхгофа, и (m-n+1) уравнений - по II закону Кирхгофа.
4.Решается система m линейных уравнений, из которой определяются токи в ветвях.
Метод контурных токов
Позволяет сократить число уравнений системы до (m-n+1).
1.Определяется число узловсхемы n и число ветвей в схеме m.
2.Произвольно выбирается направление токов во всех ветвях и одинаковое (по часовой стрелке или против часовой стрелки) направление обхода (m-n+1) контуров.
3.Задаются контурные токи 
как собственные токи каждого независимого контура схемы. Их направление совпадает с выбранным направлением обхода контура.
4.Вычисляются:
- контурные э.д.с. 
как алгебраическая сумма входящих в контур э.д.с. источников;
- собственные сопротивления 
контуров как сумма всех входящих в контур сопротивлений;
- общие сопротивления 
контуров как сумма сопротивлений двух смежных контуров.
5.Составляется система из (m-n+1) уравнений по II закону Кирхгофа, в которых справа – контурные э.д.с., а слева – сумма падений напряжения, созданного контурным током своего контура на собственном сопротивлении контуров (со знаком «+») и созданных контурными токами смежных контуров на общих сопротивлениях контуров (со знаком «-»).
6.Решается система (m-n+1) линейных уравнений, из которых определяются контурные токи.
7.Определяются токи в ветвях через контурные токи. В ветвях, общих для смежных контуров, токи равны алгебраической сумме соответствующих контурных токов:
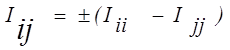
Метод узловых потенциалов
Позволяет сократить число уравнений до (n-1).
1.Определяется число узлов схемы n.
2.Произвольно выбирается направление токов во всех ветвях.
3.Выбирается базовый узел, потенциал которого принимается равным нулю. (Целесообразно выбрать базовым узел, к которому примыкает максимальное число ветвей).
4.Определяются:
- собственные проводимости 
(n-1) узлов как сумма проводимостей всех примыкающих к узлу ветвей;
- общие проводимости 
между двумя узлами 
и j как сумма проводимостей между ними;
- узловые токи 
как алгебраическая сумма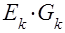 
, где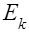 
- э.д.с. к- ой ветви, примыкающей к к- ому узлу (
, если направлена к - тому узлу), 
- проводимость к- ой ветви.
5.Составляется система из (n-1) уравнений по I закону Кирхгофа, в которых справа – узловые токи, а слева – сумма потенциала собственного узла, умноженного на собственную проводимость узла (со знаком «+») и потенциалов смежных узлов, умноженных на общую проводимость между узлами (со знаком «-»).
6.Решается система (n-1) уравнений, из которой определяются потенциалы узлов по формулам.
8.Определяются токи в ветвях через потенциалы узлов:
,
где 
, если к- тый ток течет от узла к узлу j;
, если совпадает по направлению с к- тым током.
Метод наложения токов
Позволяет свести расчет разветвленной электрической цепи с несколькими источниками питания к нескольким расчетам этой же цепи с одним источником питания.
1. Составляются частные схемы, в каждой из которых оставляют один источник э.д.с., замыкая все остальные накоротко.
2. Выбираются направления токов в ветвях частной схемы в зависимости от направления действующего в ней источника э.д.с.
3. Рассчитывают токи 
в ветвях частной схемы, применяя метод «свертывания цепи», т.е. ее постепенного упрощения путем замены сложного соединения резисторов эквивалентными сопротивлениями и сведения схемы к одному эквивалентному сопротивлению. При расчете токов в ветвях схему «разворачивают» в обратном порядке.
4. Определяются токи 
в ветвях исходной схемы как алгебраическая сумма токов в ветвях частной схемы, причем 
, если совпадает с направлением в исходной схеме, и наоборот.
