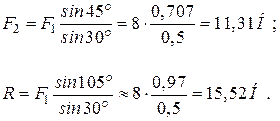Линейными операциями называются операции сложения и вычитания векторов и умножения вектора на число. Отметим, что для скалярных и векторных величин правила сложения и вычитания разные.
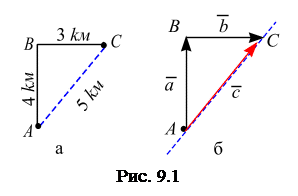 Рассмотрим пример (рис. 9.1, а). Для того чтобы попасть из точки А в некоторую точку С, путник сначала проходит путь АВ, до которого 4 kм, затем путь ВС, равный 3 kм и попадает в пункт С; при этом он проходит путь, который вычисляется алгебраическим сложением
Рассмотрим пример (рис. 9.1, а). Для того чтобы попасть из точки А в некоторую точку С, путник сначала проходит путь АВ, до которого 4 kм, затем путь ВС, равный 3 kм и попадает в пункт С; при этом он проходит путь, который вычисляется алгебраическим сложением
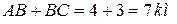 .
.
Расстояние между пунктами А и С можно вычислитьпо теоремеПифагора(рис. 9.1, а):
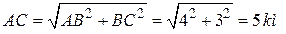 .
.
Определим путь АВ вектором  , где
, где 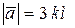 ; путь
; путь 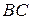 – вектором
– вектором 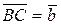 , где
, где 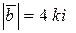 . Тогда путь
. Тогда путь 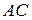 определим вектором
определим вектором 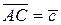 , где
, где 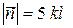 (рис. 2.1, б). Из рис. 9.1, б видно, что вектор
(рис. 2.1, б). Из рис. 9.1, б видно, что вектор  соединяет начало вектора
соединяет начало вектора  с концом вектора
с концом вектора 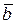 . Треугольник АВС (рис. 9.1, б) называется векторным треугольником.
. Треугольник АВС (рис. 9.1, б) называется векторным треугольником.
Вектор  называется суммой векторов
называется суммой векторов  и
и 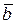 . В этом случае пишут:
. В этом случае пишут:
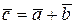 . (1)
. (1)
В общем случае, при сложении двух векторов, приложенных в одну точку А, используют так называемое «правило параллелограмма».
Пример 9. 1. Заданы два вектора  и
и 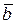 , то есть заданы модули векторов:
, то есть заданы модули векторов:  ,
, 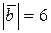 , а направления векторов относительно оси
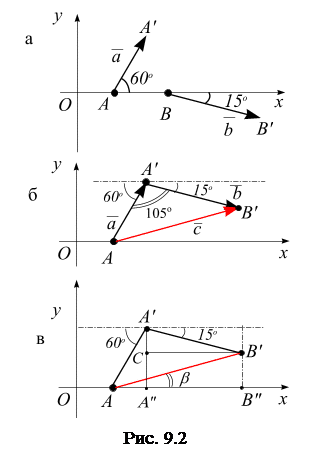
, а направления векторов относительно оси  показаны на рис. 9.2, а. Сложить геометрически заданные векторы.
показаны на рис. 9.2, а. Сложить геометрически заданные векторы.
Решение. Параллельным переносом совместим начало вектора 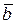 с концом вектора
с концом вектора  (рис. 9.2, б). Вектор
(рис. 9.2, б). Вектор  соединит начало вектора
соединит начало вектора  (точку
(точку  ) с концом вектора
) с концом вектора 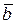 (точкой
(точкой 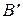 ), получим вектор
), получим вектор  , который является суммой векторов
, который является суммой векторов  и
и 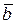 :
:
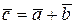 .
.
 Вычислим модуль и направление полученного геометрически вектора
Вычислим модуль и направление полученного геометрически вектора  . Для этого вычислим угол
. Для этого вычислим угол 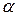 (рис. 9.2, б):
(рис. 9.2, б):
 .
.
По формуле приведения имеем
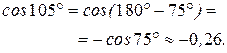
Используя теорему косинусов для 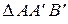 , вычислим модуль вектора
, вычислим модуль вектора  (рис. 9.2, б):
(рис. 9.2, б):
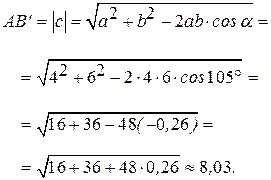
Определим направление вектора  относительно оси
относительно оси  , т. е. вычислим угол
, т. е. вычислим угол 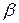 , рис. 9.2, в.
, рис. 9.2, в.
Геометрия задачи (рис. 9.2, б).
Рассмотрим 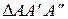 . Угол
. Угол 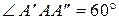 , тогда
, тогда
 .
.
Рассмотрим 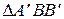 . Угол
. Угол 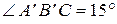 , тогда
, тогда
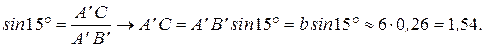
Вычислим длину отрезка 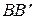 :
:
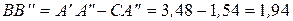 .
.
Рассмотрим 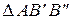 :
:
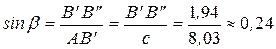 ;
;
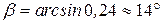 .
.
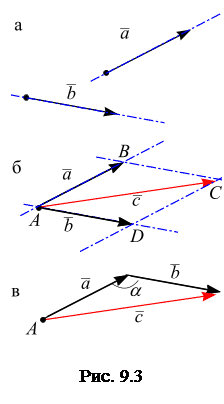 Геометрическим построением векторов можно убедиться в правильности вычислений, измерив линейкой сторону с параллелограмма и транспортиром угол
Геометрическим построением векторов можно убедиться в правильности вычислений, измерив линейкой сторону с параллелограмма и транспортиром угол 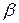 .
.
Правило параллелограмма. Пусть  и
и 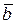 – два свободных вектора (рис. 9.3, а). Выберем произвольно точку А. Параллельным переносом векторов
– два свободных вектора (рис. 9.3, а). Выберем произвольно точку А. Параллельным переносом векторов  и
и 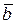 , совместим их начало с точкой
, совместим их начало с точкой  (рис. 9.3, б). Построим на этих векторах, как на сторонах, параллелограмм
(рис. 9.3, б). Построим на этих векторах, как на сторонах, параллелограмм 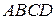 . Для этого из конца вектора
. Для этого из конца вектора  проведем прямую, параллельную линии действия вектора
проведем прямую, параллельную линии действия вектора 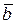 ; из конца вектора
; из конца вектора 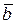 проведем прямую, параллельную линии действия вектора
проведем прямую, параллельную линии действия вектора  . Эти прямые пересекутся в точке
. Эти прямые пересекутся в точке 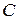 . Вектор
. Вектор  , соединяющий точки А и С параллелограмма, является суммой векторов
, соединяющий точки А и С параллелограмма, является суммой векторов  и
и 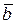 :
:
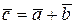 .
.
Полученный параллелограмм состоит из двух равных треугольников: 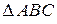 и
и 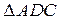 . Если вектор
. Если вектор 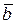 параллельным переносом совместим с прямой
параллельным переносом совместим с прямой 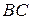 , получим правило сложения векторов (1) – правило векторного треугольника, рис. 9.3, в.
, получим правило сложения векторов (1) – правило векторного треугольника, рис. 9.3, в.
Операция сложения векторов обладает переместительным (коммутативным) свойством
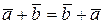 .
.
Модуль вектора  вычисляется по теореме косинусов (рис. 9.3, в)
вычисляется по теореме косинусов (рис. 9.3, в)
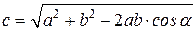 .
.
Итак, сложение двух векторов можно выполнить двумя способами: построением параллелограмма или построением векторного треугольника. Оба графических построения дают один и тот же результат.
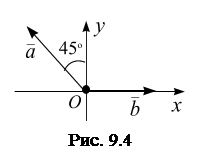 Пример 9.2. Заданы два вектора
Пример 9.2. Заданы два вектора  и
и 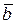 :
:  ,
,  , направления векторов относительно оси
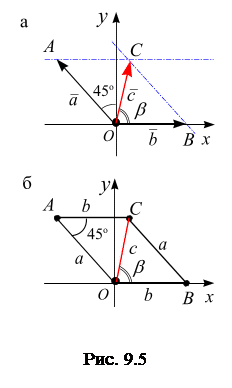
, направления векторов относительно оси  показаны на рис. 9.4. Сложить заданные векторы по правилу параллелограмма.
показаны на рис. 9.4. Сложить заданные векторы по правилу параллелограмма.
Решение. По условию задачиначало векторов  и
и 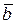 совпадают, рис. 9.5. Из конца вектора
совпадают, рис. 9.5. Из конца вектора  проведем прямую, параллельную линии действия вектора
проведем прямую, параллельную линии действия вектора 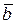 ; из конца вектора
; из конца вектора 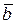 проведем прямую, параллельную линии действия вектора
проведем прямую, параллельную линии действия вектора  . Эти прямые пересекутся в точке
. Эти прямые пересекутся в точке 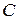 . Вектор
. Вектор  , соединяющий точки А и С параллелограмма, является суммой векторов
, соединяющий точки А и С параллелограмма, является суммой векторов  и
и 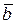 :
:
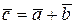 .
.
Геометрия задачи (рис. 9.5)
Рассмотрим 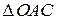 . Угол
. Угол 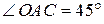 , тогда используя теорему косинусов для
, тогда используя теорему косинусов для 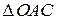 , вычислим модуль вектора
, вычислим модуль вектора  (рис. 9.5, б):
(рис. 9.5, б):
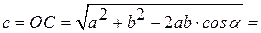
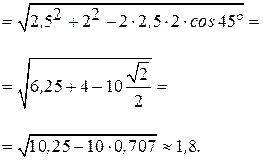
Определим направление вектора  относительно оси
относительно оси  , т. е. вычислим угол
, т. е. вычислим угол 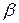 , рис. 9.5, б.
, рис. 9.5, б.
Рассмотрим 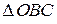 . Угол
. Угол 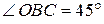 , тогда, используя теорему синусов для
, тогда, используя теорему синусов для 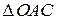 , получим
, получим
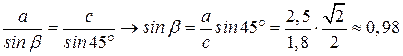 ;
;
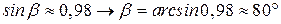 .
.
Геометрическим построением векторов можно убедиться в правильности вычислений, измерив линейкой сторону с параллелограмма и транспортиром угол 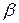 . Используя понятия вектора и правила их сложения, можно моделировать и решать реальные физические задачи.
. Используя понятия вектора и правила их сложения, можно моделировать и решать реальные физические задачи.
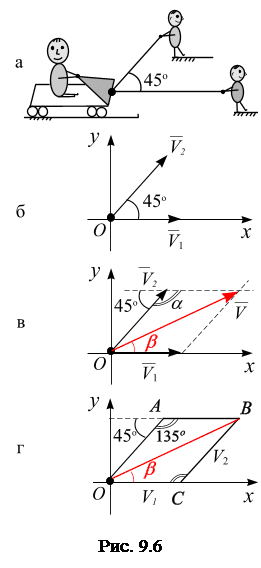
Пример 9.3. Два мальчикакатают на тележке третьего мальчика. Первый мальчик катит тележку в плоскости по горизонтали со скоростью  , второй – под углом
, второй – под углом  к нему со скоростью
к нему со скоростью  (рис. 9.6, а). Вычислить направление движения тележки.
(рис. 9.6, а). Вычислить направление движения тележки.
Решение. Скорость движения любого объекта являетсявекторной величиной, т.к.она определяет и направление движения, и изменение пройденного пути со временем, т. е. величину скорости.
 Поэтому направление движения тележки определяется направлением вектора скорости тележки
Поэтому направление движения тележки определяется направлением вектора скорости тележки  .
.
Изобразим скорость движения мальчиков, катающих тележку через векторы, направление которых задано, рис. 9.6, б.
Вычислим направление скорости тележки. Сложим геометрически векторы  и
и 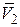 , отложенные в масштабе 1:2 от точке
, отложенные в масштабе 1:2 от точке 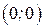 , рис. 9.6, в:
, рис. 9.6, в:
 .
.
Геометрия задачи
Рассмотрим 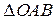 и вычислим угол
и вычислим угол 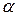 (рис. 9.6, в):
(рис. 9.6, в):
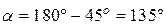 .
.
Используя теорему косинусов для 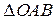 , вычислим модуль вектора
, вычислим модуль вектора 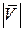 (рис. 9.6, в):
(рис. 9.6, в):
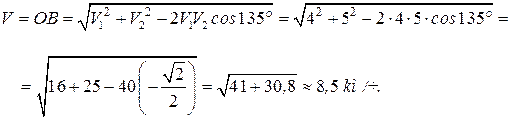
Определим направление движения тележки оси  , т. е. вычислим угол
, т. е. вычислим угол 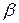 , рис. 2.6, г.
, рис. 2.6, г.
Рассмотрим 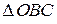 . Угол
. Угол 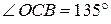 , тогда, используя теорему синусов для
, тогда, используя теорему синусов для 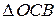 , получим
, получим
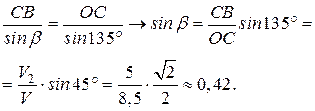
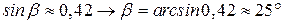 .
.
Измерив полученную диагональ (рис.9.6,в), убедимся, что 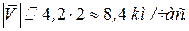 Измерив транспортиром угол
Измерив транспортиром угол 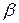 , убедимся, что
, убедимся, что 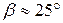 .
.
 Пример 9. 4. Вертикально падающие капли дождя оставляют на боковых стеклах автомобиля полосы под углом
Пример 9. 4. Вертикально падающие капли дождя оставляют на боковых стеклах автомобиля полосы под углом 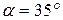 к вертикали, рис. 9.7. Скорость движения автомобиля 60 км/ч. Определить, с какой скоростью падают капли дождя.
к вертикали, рис. 9.7. Скорость движения автомобиля 60 км/ч. Определить, с какой скоростью падают капли дождя.
Решение. Изобразим движение автомобиля, капель дождя на стекле автомобиля, и сам дождь через векторы, направление которых задано, рис. 9.7. Дождь на автомобиль падает вертикально, следовательно, вектор скорости выбранной капли направлен вертикально, обозначим скорость как вектор  ; относительно Земли скорость автомобиля обозначим вектором
; относительно Земли скорость автомобиля обозначим вектором  : скорость движения капли дождя по боковому стеклу автомобиля обозначим через вектор
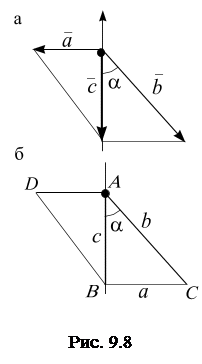
: скорость движения капли дождя по боковому стеклу автомобиля обозначим через вектор 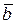 (рис. 9.8, а). Тогда вектор скорости капли дождя
(рис. 9.8, а). Тогда вектор скорости капли дождя  можно представить в виде геометрической суммы векторов
можно представить в виде геометрической суммы векторов  и
и 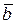 .
.
 По условию задачи известно, что
По условию задачи известно, что 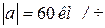 ,
, 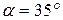 .
.
Геометрия задачи
Диагональ параллелограмма 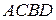 делит его на два равных треугольника, рис. 9.8, б.
делит его на два равных треугольника, рис. 9.8, б.
Рассмотрим 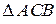 :
:
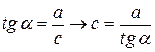 .
.
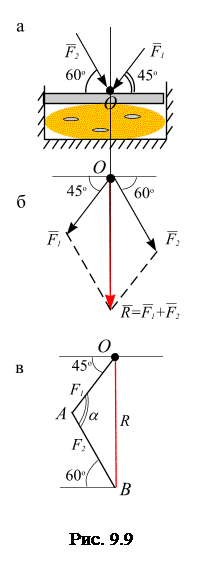 Подставим заданные значения, получим скорость падающей капли дождя:
Подставим заданные значения, получим скорость падающей капли дождя:
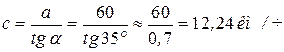 .
.
Пример 9.5. На пресс, сжимающий головку сыра, в точке О приложены две силы  и
и 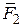 (рис. 9.9). Вычислить модуль равнодействующей силы
(рис. 9.9). Вычислить модуль равнодействующей силы  , сжимающей головку сыра, если она направлена вертикально. Вычислить модуль силы
, сжимающей головку сыра, если она направлена вертикально. Вычислить модуль силы 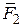 . Дано:
. Дано:  ,
, 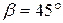 ,
,  .
.
Решение. Изобразим действующие на пресс силы через векторы, направление которых задано, рис. 9.9, б. Геометрическая сумма заданных сил равна равнодействующей силе  , которую вычислим по правилу параллелограмма:
, которую вычислим по правилу параллелограмма:
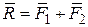 .
.
Диагональ параллелограмма, построенного на векторах, как на сторонах, делит параллелограмм на два равных треугольника. Рассмотрим 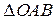 ,
,
рис. 9.9, б:
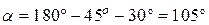 .
.
По теореме синусов, получаем
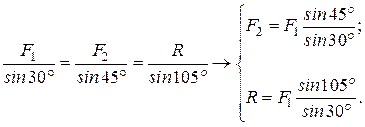 .
.
Здесь
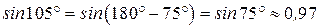 ;
; 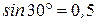 .
.
Итак,