а) Найти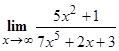 
.
Решение. Прежде всего, проверим, применимы ли к данной дроби теоремы о пределах, или мы имеем дело с неопределенностью. Для этого найдем пределы числителя и знаменателя дроби. Функции 
и 
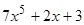являются бесконечно большими. Поэтому, 
, 
.
Следовательно, имеем дело с неопределенностью вида 
.
Для раскрытия этой неопределенности и использовании теоремы о пределе отношения двух функций выделим в числителе и в знаменателе 
в старшей для числителя и знаменателя степени в качестве сомножителя и сократим дробь.
Ответ. 0.
Вычислить пределы функций.
а) Найти 
.
Решение. Для раскрытия неопределенности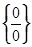 
в этом случае, нужно умножить числитель и знаменатель на выражение, сопряженное числителю, а затем сократить дробь на общий множитель.
Ответ. 
.
Вычислить пределы функций.
а) Найти 
.
Решение. Для раскрытия неопределенности 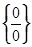в этом случае, нужно выделить первый замечательный предел: 
Ответ. k
б) Найти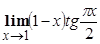 
.
Решение. Для раскрытия неопределенности 
в этом случае, нужно произведение преобразовать в частное, то есть неопределенность свести к неопределенност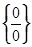и или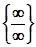 
.
Выделяем первый замечательный предел, то есть, умножаем числитель и знаменатель на 
. Получаем,
.
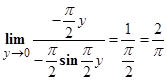Ответ. 
.
Вычислить пределы функций.
а) Найти 
.
Решение. Для раскрытия неопределенности 
в этом случае, нужно выделить второй замечательный предел: 
.
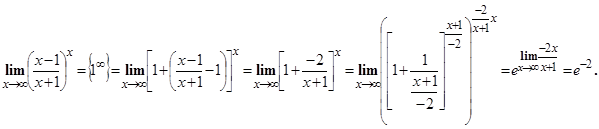
Ответ. 
.
б) Найти 
Решение. Для раскрытия неопределенности 
в этом случае, нужно выделить второй замечательный предел: 
.
Ответ. 
.
ПРАКТИЧЕСКАЯ РАБОТА. Вычисление предела функции, раскрытие простейших неопределенностей.
ЦЕЛЬ РАБОТЫ:
научиться раскрывать неопределенность вида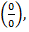 
путем разложения на множители; научиться раскрывать неопределенность вида 
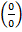, вызванную присутствием корня; научиться вычислять пределы при 
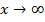, в том числе путем раскрытия неопределенностей вида 
и 
.
Методические указания к выполнению практической работы.
Теоретическая часть.
Раскрытие неопределенности вида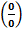 
Теоретическая часть:
Способы разложения на множители:
1) Вынесение общего множителя за скобку: 
2) Формулы сокращенного умножения:
- Разность квадратов
-
-
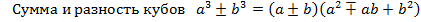
3) Разложение квадратного трехчлена на множители:
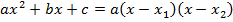, где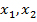 
корни квадратного уравнения
4) Способ группировки
- Образовать группы, между ними знак «+»,
- В каждой группе вынести общий множитель за скобки,
- Найти и вынести за скобки общий множитель обеих групп, в результате получим произведение множителей.
Разбор решения одного варианта:
| 
|
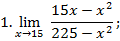
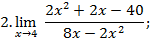
Решение:
подстановка предельного значения 
дает неопределенность вида .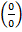
Чтобы раскрыть эту неопределенность надо разложить числитель и знаменатель на множители. В числителе вынесем общий множитель «х» за скобку, в знаменателе заметим, что 
применим формулу разность квадратов
сократим на множитель, приводящий к неопределенности, это х-15
подстановка 
дает
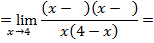
тогда
В числителе вынесем общий множитель «x» за скобки, причем заметим, что 121= 
, и применим формулу разность квадратов
А в знаменателе увидим формулу сокращенного умножения: квадрат первого, минус удвоенное произведение первого на второе, плюс квадрат второго
Сократим на множитель (х-11)
Подставив предельное значение 
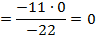
В числителе применим формулу разность кубов 
, а в знаменателе разложим квадратный трехчлен на множители
, тогда
сократим на 
и подставим 
, получим
в числителе разложим на множители способом группировки
А в знаменателе вынесем за скобки общий множитель «х»
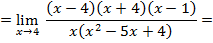
А затем разложим квадратный трехчлен на множители:
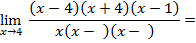
сократим на 
и подставим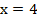 
Раскрытие неопределенности вида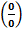
Теоретическая часть:
Сопряженными называются множители 
, причем их произведение дает формулу разность квадратов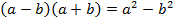 
Согласно свойств степени и корня: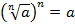 
Пример 1: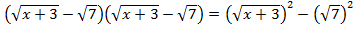 
= 
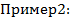
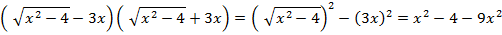
Разбор решения одного варианта:
 
| 
|
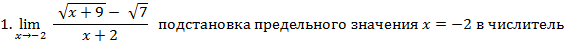
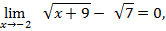
предел знаменателя дает
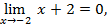
то имеет место неопределенность вида 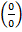, которая вызвана присутствием корня. Раскроем неопределенность умножением числителя и знаменателя на сопряженный множитель к числителю
применив в числителе формулу разность квадратов
имеем:
при возведении квадратного корня в квадрат корень исчезает
сократив на 
- множитель, приводящий к неопределенности и подставив предельное значение 
имеем
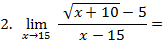
подстановка дает неопределенность вида 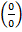, вызванную присутствием корня, поэтому умножаем на сопряженный множитель к числителю
применив в числителе, формулу разность квадратов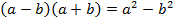
Посчитав, в числителе подобные, имеем
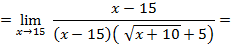
Сократим числитель и знаменатель на множитель x-15
подставим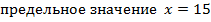 
, тогда
подстановка предельного значения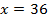 
дает неопределенность вида 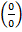, умножаем числитель и знаменатель на сопряженный множитель к знаменателю
в знаменателе формула разность квадратов 
вынесем в числителе общий множитель «х» за скобку, а в знаменателе вычислим
сократим на 
и подставим 
имеем
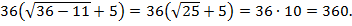
умножаем на сопряженный к числителю, а затем в числителе применяем формулу разность квадратов :
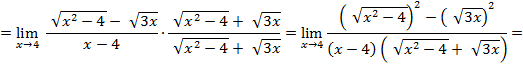
в числителе квадратный трехчлен, разложим на множители по формуле:
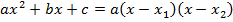, где 
сократим на 
и подставим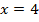 
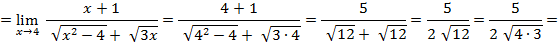
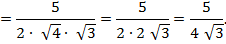
Вычисление предела при 
.
Теоретическая часть:
- Предел бесконечно малой равен нулю.
- Если предел величины равен нулю, то эта величина есть бесконечно малая.
- Предел бесконечно большой величины равен бесконечности.
- Если
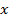- величина бесконечно малая, то обратная ей величина 
является бесконечно большой. - Если 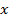- величина бесконечно большая, то обратная ей величина является бесконечно малой.
- Предел числа есть само число.
- Произведение постоянной величины на бесконечно малую есть величина бесконечно малая.
Разбор решения одного варианта:
| 
|
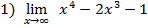
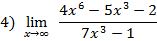
первые два слагаемых 
пределов не имеют, поэтому имеет место неопределенность 
, чтобы её раскрыть, надо
вынести за скобку большую степень переменной, входящей в пример:
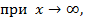величины 
предел числителя и предел знаменателя есть величины бесконечно большие 
имеет место неопределенность вида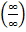 
, раскроем её делением числителя и знаменателя на наибольшую степень переменной т.е. на 
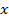и сократим, тогда
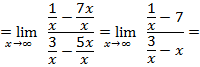
помня, что при ,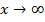 
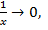
, имеем
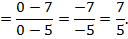
делим каждое слагаемое на 
сократим
, 
, 
, 
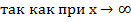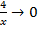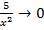имеем:
делим числитель и знаменатель на старшую степень переменной, это 
:
, 
, 
, 
, 
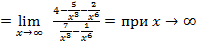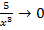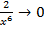тогда предел числителя равен 4,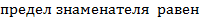 
0, т.е. в знаменателе бесконечно малая величина вся дробь есть величина бесконечно большая, т.е. = 
.
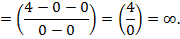
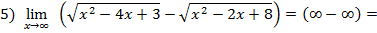
умножим на сопряженный
при 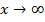, имеем 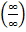, раскроем путем деления на 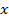, т.к. 
:
тогда: 
