ПРАКТИЧЕСКАЯ РАБОТА. Предел и непрерывность функции.
ЦЕЛЬ РАБОТЫ: исследовать функцию на непрерывность в точках;
находить точки разрыва и определять их род;
научиться раскрывать неопределенность вида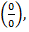 
путем разложения на множители; научиться раскрывать неопределенность вида 
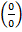, вызванную присутствием корня; научиться вычислять пределы при 
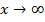, в том числе путем раскрытия неопределенностей вида 
и 
; научится раскрывать неопределенность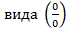 
с помощью первого замечательного предела, вычислять пределы, содержащие тригонометрические функции; научиться раскрывать неопределенность вида 
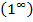путем применения второго замечательного предела.
Методические указания к выполнению практической работы.
Теоретическая часть.
Раскрытие неопределенности вида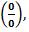 
путем разложения на множители:
Способы разложения на множители:
1) Вынесение общего множителя за скобку: 
2) Формулы сокращенного умножения:
Разность квадратов 
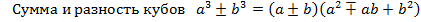
3) Разложение квадратного трехчлена на множители:
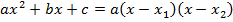, где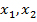 
корни квадратного уравнения
4) Способ группировки
Образовать группы, между ними знак «+»,
В каждой группе вынести общий множитель за скобки,
Найти и вынести за скобки общий множитель обеих групп, в результате получим произведение множителей.
Раскрытие неопределенности вида 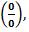вызванная присутствием корня:
Сопряженными называются множители 
, причем их произведение дает формулу разность квадратов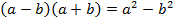 
Согласно свойств степени и корня: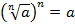 
Пример 1: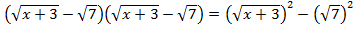 
= 
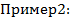
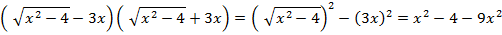
Вычисление пределов при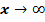 
, в том числе путем раскрытия неопределенностей вида и :
Предел бесконечно малой равен нулю.
Если предел величины равен нулю, то эта величина есть бесконечно малая.
Предел бесконечно большой величины равен бесконечности.
Если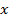 
- величина бесконечно малая, то обратная ей величина 
является бесконечно большой.
Если 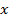- величина бесконечно большая, то обратная ей величина является бесконечно малой.
Предел числа есть само число.
Произведение постоянной величины на бесконечно малую есть величина бесконечно малая.
Вычисление пределов, содержащих тригонометрические функции:
Предел отношения синуса бесконечно малого угла к самому углу, есть величина постоянная, равная единице, т.е.
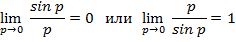
Раскрытие неопределенности вида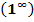 
путем применения второго замечательного предела:
Предел суммы единицы и бесконечно малой величины, в степени бесконечно большой, есть величина постоянная, равная числу Эйлера 
.
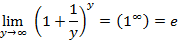
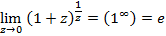
Решение типового варианта практической работы.
Вычислить пределы функций.
а) Найти 
Решение. Для вычисления данного предела подставим значение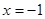 
в функцию, стоящую под знаком предела. Получим,
.
Ответ. -3.
б) Найти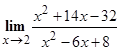 
.
Решение. Для раскрытия неопределенности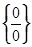 
в этом случае, нужно разложить числитель и знаменатель на множители и сократить дробь на общий множитель.
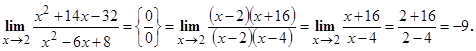
Ответ. -9.
