Задача 1. Парная регрессия и корреляция.
Месячные объемы продаж зерна (Х, центнеров) и величины премиального фонда (Y, тыс. руб.) в девяти отпускных пунктах элеватора, характеризуются следующими данными (таблица 1).
Таблица1
| Объем продаж | у | 6,1 | 8,2 | 7,1 | 14,9 | 9,1 | 9,0 | 15,8 | 8,2 | 7,7 |
| Премиальный фонд | х | 2,3 | 2,8 | 1,9 | 3,4 | 2,6 | 3,3 | 4,2 | 3,0 | 1,7 |
Исследовать зависимость премиального фонда от объема продаж, используя линейную зависимость. Получить прогноз объема премиального фонда при продажах 4,5 центнера зерна. Оценить качество прогноза. Продавцы полагают, что если объем продаж составит 5 центнеров, то их премия будет свыше 18 тыс. руб. в месяц. Найти вероятность данного предположения.
Решение:
1. Построим поле корреляции (рис.1).
2. Для расчета параметров уравнения линейной регрессии построим расчетную таблицу (Таблица 2).
Рис. 1 Поле корреляции.
Таблица 2
| y | х | x*y | y2 | x2 | 
| 
| Ai | |
| 6,1 | 2,3 | 14,03 | 37,21 | 5,29 | 7,795 | -1,695 | 1,70% | |
| 8,2 | 2,8 | 22,96 | 67,24 | 7,84 | 9,57 | -1,37 | 1,37% | |
| 7,1 | 1,9 | 13,49 | 50,41 | 3,61 | 6,375 | 0,725 | 0,73% | |
| 14,9 | 3,4 | 50,66 | 222,01 | 11,56 | 11,7 | 3,2 | 3,20% | |
| 9,1 | 2,6 | 23,66 | 82,81 | 6,76 | 8,86 | 0,24 | 0,24% | |
| 3,3 | 29,7 | 10,89 | 11,345 | -2,345 | 2,34% | |||
| 15,8 | 4,2 | 66,36 | 249,64 | 17,64 | 14,54 | 1,26 | 1,26% | |
| 8,2 | 24,6 | 67,24 | 10,28 | -2,08 | 2,08% | |||
| 7,7 | 1,7 | 13,09 | 59,29 | 2,89 | 5,665 | 2,035 | 2,04% | |
| Итого | 86,1 | 25,2 | 258,55 | 916,85 | 75,48 | 86,13 | - | 14,95% |
| Среднее значение | 9,57 | 2,8 | 28,73 | 101,87 | 8,39 | - | - | 1,66 |
| 3,21 | 0,74 | - | - | - | - | - | - |
| 10,2851 | 0,55 | - | - | - | - | - | - |
Коэффициенты уравнения регрессии определим по формулам (1.1), (1.2):
, 
.
Используя данные расчетной таблицы (Таблица 2), получим значение коэффициентов a, b уравнения регрессии:
.
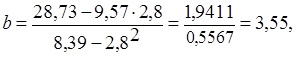
Таким образом, уравнение регрессии имеет вид: 
.
Экономический анализ решения регрессии показывает, что с увеличением продажи зерна на 1 центнер, премиальный фонд возрастает в среднем на 3,55 тыс. руб.
3. Тесноту линейной связи между изучаемыми показателями оценит коэффициент корреляции rxy и детерминации R2. Для расчета rxy и R2 вычислим дисперсии факторов х, у по формулам (1.3), (1.4), (1.5):
Величина дисперсии факторов x,y для наших данных:
| 
|
| 
|
Коэффициент корреляции rxy устанавливает количественную меру тесноты связи и формирует качественную характеристику силы связи: 
Коэффициент корреляции 
по шкале Чеддока (Приложение 3) связь между изучаемыми факторами высокая.
Найдем коэффициент детерминации:
Экономический смысл этого означает, что 65,61% вариации объема продаж (y) объясняется вариацией фактора премиального фонда (х).
4. Вычислим значения 
по полученному уравнению регрессии:
| 2,3 | 2,8 | 1,9 | 3,4 | 2,6 | 3,3 | 4,2 | 3,0 | 1,7 |
|
| 7,795 | 9,57 | 6,375 | 11,7 | 8,87 | 11,33 | 14,54 | 10,28 | 5,665 |
Найдем среднюю ошибку аппроксимации, которая определяет качество полученной модели. Для расчета используются формулы (1.7), (1.8):
Например, для первой строки данных таблицы имеем:
Аналогично найдем значения 
для всех строк 
. В результате получаем величину ошибки аппроксимации для нашей задачи:
где 
Качество построенной модели оценивается как хорошее, так как фактическое значение 
не превышает 8-10%.
5. Оценку статистической значимости уравнения регрессии в целом проведем с помощью F-критерия Фишера. Фактическое значение F-критерия вычисляется по формулам (1.9) или (1.10).
Фактическое значение F -критерия Фишера сравнивается с табличным значением Fтабл(a; k1; k2) (Приложение 2)при уровне значимости α и степенях свободы k1 = m и k2 = n - m -1. При этом, если фактическое значение F – критерия больше табличного, то признается статистическая значимость уравнения в целом.
Табличное значение критерия при 
и степенях свободы k1 =1 и k2 =9 - 2 =7 составляет Fтабл= 5,59. Для расчета фактического значения F-критерия Фишера используем формулу (1.10). Имеем:
.
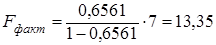Сравниваем полученное значение с табличным:
Fфакт =13,35> Fтабл = 5,59.
Так как, полученное (фактическое) значение больше табличного, то уравнение регрессии признается статистически значимым и может использоваться для прогноза премиального фонда.
Оценку статистической значимости параметров регрессии проведем с помощью t -статистики Стьюдента.
Табличное значение (Приложение 4) t -критерия для числа степеней свободы df = n - 2 =9 - 2 =7 и уровня значимости a = 0,05 составит tтабл = 2,36.
Определим случайные ошибки параметров ma, mb и коэффициента корреляции 
по формулам (1.12), (1.13), (1.14):
Предварительно найдем выборочную остаточную дисперсию
Тогда 
| (1.12) | 
|
| (1.13) | 
|
| (1.14) | 
|
Фактическая t-статистика определяется по формулам (1.11). Расчеты фактической t-статистики Стьюдента приведены ниже:
| 
| 
|
Сравниваем полученные значения с табличным значением. В результате имеем:
Видим, что фактическое значение t-статистики коэффициента а не превосходит табличное, то есть коэффициент а незначим. Фактические значения t-статистики параметров b и rxy превосходят табличное, а следовательно, онине случайно отличаются от нуля и статистически значимы.
6. Найдем прогнозное значение премиального фонда при х = 4,5. По уравнению регрессии находим
тыс. руб.
7. Найдем прогнозное значение премиального фонда при х = 5. По уравнению регрессии находим
тыс. руб.
Определим доверительный интервал для данного индивидуального прогноза
.
Тогда доверительный интервал:
.
Искомую вероятность определим, используя нормальный закон распределения с параметрами 
.
.
Построим в поле корреляции полученное уравнение линейной регрессии (рис.2).
Рис 2.
Как видно, на графике большинство точек поля корреляции расположены вдоль расчетной теоретической прямой , следовательно, полученное нами уравнение регрессии может использоваться для рассмотрения определенных вопросов, относящихся к исследуемому процессу.
Решение данной задачи можно проверить, используя возможности MS Excel с помощью инструмента анализа данных Регрессия.
Рассмотрим данную задачу в MS Excel 2010.
По умолчанию эта надстройка отключена. Для ее активации необходимо выполнить следующие действия.
1. Активируем вкладку Файл, в открывшемся меню ищем пункт Параметры и кликаем на него.
2. В открывшемся окне, слева, следует активировать пункт Надстройки, выделить Пакет анализа и нажать на кнопку Перейти.
3. Всплывающее окошко предложит выбрать доступные надстройки, в нем необходимо поставить галочку напротив Пакет анализа, а затем подтвердить выбор кликнув по кнопочке ОК.
После активации надстройки Пакета анализа она будет всегда доступна во вкладке главного меню Данные под ссылкой Анализ данных.
В активном окошке инструмента Анализа данных из списка возможностей ищем и выбираем Регрессия
Далее откроется окошко для настройки и выбора исходных данных для вычисления параметров регрессионной модели. Здесь нужно указать интервалы исходных данных, а именно описываемого параметра (Y) и влияющих на него факторов (Х), как это на рисунке ниже, остальные параметры, в принципе, необязательны к настройке.
После того как выбрали исходные данные и нажали ОК, MS Excel выдает расчеты на новом листе активной книги (если в настройках не было выставлено иначе), эти расчеты имеют следующий вид:
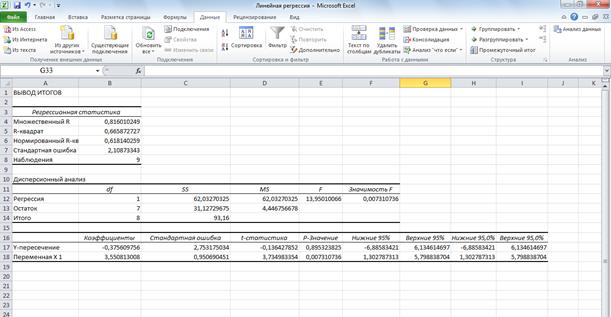
Соберем рассчитанные коэффициенты в модель:
.
Как видим полученное нами уравнение рассчитано верно.
