Краткий теоретический материал

Линейная парная регрессия

Краткий теоретический материал

При изучении конкретных экономических ситуаций в большинстве случаев существует статистическая зависимость.

Определение: Зависимость между двумя переменными, когда каждому значению одной из них соответствует определенное (условное) распределение другой называется статистической.

Среди статистических зависимостей выделяют корреляционную зависимость.

Определение: Зависимость между двумя переменными, когда каждому значению одной из них соответствует математическое ожидание (среднее значение) другой называется корреляционной.

Частным случаем корреляционной зависимости является регрессионная зависимость, т.е. тогда когда рассматривается односторонняя зависимость случайной величины Y– зависимая (объясняемая, выходная, эндогенная) переменная от неслучайной величины Х – независимая (объясняющая, входная, экзогенная) переменная. Например, зависимость потребления от дохода, спроса от цены, объема чистого экспорта от курса валют, инвестиций от величины процентной ставки и т.д.

Такая зависимость не является однозначной в том смысле, что каждому конкретному значению объясняющей переменной соответствует некоторое вероятностное распределение зависимой переменной. Поэтому осуществляют анализ, как объясняющая переменная влияет на зависимую переменную «в среднем».

Термин «регрессия» (движение назад, возвращение в прежнее состояние) был введен английским ученым Фрэнсисом Галтоном в конце XIX в. при анализе зависимости между ростом родителей и ростом детей. Галтон заметил, что рост детей у очень высоких родителей в среднем меньше, чем средний рост родителей. У очень низких родителей, наоборот, средний рост детей выше. И в том, и в другом случае средний рост стремится (возвращается) к среднему росту людей в данном регионе. Отсюда и выбор термина, отражающего такую зависимость.

Регрессионный анализ включает следующие этапы:

1)определение вида функции, описывающей функциональную связь между результативным признаком и факторными признаками;

2)определение коэффициентов регрессии, то есть числовых параметров, входящих в уравнение регрессии;

3)расчет теоретических значений результативного признака для отдельных наборов значений факторов;

4)исследование отклонений расчетных значений от эмпирических данных;

5)оценка качества полученной модели и проверка соответствующих гипотез о регрессии.

При рассмотрении зависимости двух случайных величин говорят о парной регрессии. Зависимость нескольких переменных называется множественной регрессией.

Основной целью построения регрессии является предсказание (прогнозирование) среднего значения (зависимой переменной) при фиксированных значениях независимых переменных.

Среди различных видов регрессионных зависимостей наиболее важными являются линейные, так как они достаточно просты и встречаются во многих зависимостях между экономическими переменными. Ограничимся рассмотрением линейной парной регрессии.

Парная регрессия – уравнение связи двух переменных :

где y – зависимая переменная (результативный признак);

x – независимая, объясняющая переменная (признак-фактор).

Для отражения того факта, что реальное значение зависимой переменной не всегда совпадают с ее условным математическим ожиданием и может быть различно при одном и том же значении объясняющей переменной, фактическая зависимость должна быть дополнена некоторым слагаемым , которое, по существу, является и указывает на стохастическую суть зависимости. Из этого следует, что линейная регрессия имеет следующий вид:

Присутствие случайного фактора (отклонения) в регрессионных моделях имеет следующие основные причины:

– невключение в модель всех объясняющих переменных: так, например, спрос на товар определяется его ценой, ценой на товары-заменители, доходом потребителей и т.д. Также можно перечислить такие факторы как: национальные и религиозные особенности, географическое положение региона, погода и многие другие, влияние которых приведет к некоторым отклонениям реальных наблюдений от модельных. При этом никогда заранее неизвестно, какие факторы при создавшихся условиях действительно являются определяющими, а какими можно пренебречь. Здесь уместно отметить, что в ряде случаев учесть непосредственно какой-то фактор нельзя в силу невозможности получения по нему статистических данных. Например, величина сбережений домохозяйств может определяться не только доходами всех членов семьи, но и их здоровьем, информация о котором в цивилизованных странах составляет врачебную тайну и не раскрывается. Кроме того, ряд факторов, таких как погода, носит случайный характер, что добавляет неоднозначность при рассмотрении некоторых моделей.

– неправильный выбор функциональной формы модели: из-за слабой изученности исследуемого процесса либо из-за его переменчивости может быть неверно подобрана функция, его моделирующая. Это в свою очередь скажется на отклонении модели, что отразится на величине случайного члена;

– ошибка измерений: какой бы качественной не была модель, ошибки измерений переменных отразятся на несоответствии модельных значений эмпирическим данным, что отразится на величине случайного члена;

– непредсказуемость человеческого фактора: при правильном выборе модели, скрупулезном подборе объясняющих переменных все равно невозможно спрогнозировать поведение отдельно взятого индивидуума, что в свою очередь сказывается на величине случайного члена;

Таким образом, случайный член является отражением всех причин описанных выше, а также может быть дополнен и другими.

Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). Он позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических минимальна, то есть:
.Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно a и b: Однако можно не решать данную систему, а воспользоваться готовыми формулами для нахождения b и a, вытекающие из этой системы: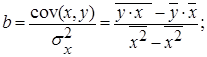

(1.1) . (1.2)

Тесноту связи, изучаемых явлений, оценивает линейный коэффициент парной корреляции r_xy. (−1 ≤ r_xy ≤ 1). Для линейной регрессии: где (1.4), (1.5). Оценка качества линейной регрессионной модели проводят с использованием коэффициента детерминации (), а также средней ошибки аппроксимации (). Коэффициент детерминации: 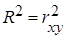(1.6.1)или (1.6.2)Коэффициент детерминации определяет какая доля вариации результативного признака (зависимая переменная), учтена в модели и обусловлена влиянием на него рассматриваемого фактора (независимая переменная). Чем ближе к единице, тем лучше качество модели. Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических: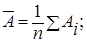

(1.7) (1.8)

Допустимый предел значений – не более 8–10%.Анализ регрессионных моделей на адекватность моделируемых случайных величин сводится к проверке предположений (статистических гипотез) о виде модели и ее параметрах. Определение: Нулевой (основной) называется выдвинутая гипотеза H_0. Определение: Конкурирующей (альтернативной) гипотезой называется гипотеза H₁, которая противоречит нулевой гипотезе H₀. Определение: Статистическим критерием называют случайную величину Т, которая служит для проверки статистических гипотез.Основные моменты проверки статистических гипотез заключаются в следующем:1. Для основной гипотезы H₀формулируется альтернативная гипотеза H₁.2. Выбирается малое положительное число – уровень значимости проверки. Обычно колеблется в пределах от 0,01 до 0,05.3. Рассматриваются теоретические выборки значений случайных величин, о которых сформулирована гипотеза H₀и выбирается случайная величина Т, называемая статистикой или тестом критерия.4. На числовой оси задается интервал D такой, что вероятность попадания теста Т в этот интервал равна . Интервал D называется областью принятия гипотезы H_0,а оставшаяся область числовой оси – критической областью. В качестве D может быть принят один из интервалов: 5. По реализациям анализируемых теоретических выборок вычисляется конкретное (наблюдаемое) значение Т и проверяется выполнение условия : если оно выполняется, то гипотеза H₀принимается в том смысле, что она не противоречит опытным данным; если не выполняется, то полагается, что гипотеза H₀ неверна и вероятность этого события определена не верно.Замечание:1. Любой критерий не доказывает справедливость проверяемой гипотезы H₀, а лишь устанавливает на принятом уровне значимости ее согласие или несогласие с данными наблюдений. 2. При проверке статистических гипотез необходимо учитывать вид исследуемого распределения и использовать соответствующие им методы (критерии).3. В итоге проверки гипотезы могут быть допущены ошибки двух родов:– ошибка первого рода состоит в том, чир будет отвергнута правильная нулевая гипотеза. Вероятность ошибки первого рода называют уровнем значимости ;– ошибка второго рода состоит в том, что будет принята неправильная нулевая гипотеза. Вероятность ошибки второго рода обозначают через .Для оценки значимости модели парной регрессии используется F-критерий Фишера. Выдвигается гипотеза H₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Далее вычисляется фактическое (F_факт) значение F-критерия Фишера и сравнивается с критическим (F_табл) значением (см. приложение 2)F_факт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы: или

где n – число единиц совокупности;

m – число параметров при переменных x.

- это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости 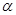. Уровень значимости - это вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно .

Если 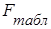< , то гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность.

Если 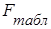> , то гипотеза не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Для оценки статистической значимости коэффициентов регрессии и корреляции используется t -критерий Стьюдента. Выдвигается гипотеза H₀ о случайной природе показателей. Далее сопоставляют их значения с величиной случайной ошибки:
(1.11).
Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяется по формулам:

(1.12),

где – выборочная остаточная дисперсия, определяющая воздействие неучтенных случайных факторов и ошибок наблюдений в модели.

(1.13)

(1.14)

Сравнивая фактическое и критическое значения t-статистики – t_табл и t_факт– принимаем или отвергаем гипотезу Н_0.

Если t_табл < t_факт, то Н₀ отклоняется, т.е. a, b и r_xy не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора x.

Если t_табл > t_факт, то гипотеза Н₀ не отклоняется и признается случайная природа формирования a, b или r_xy_..

Для значимого уравнения регрессии рассчитывают интервальные оценки параметра b и свободного члена а по следующим формулам:

(1.15) (1.16),

где Т_кр определяется по таблице распределения Стьюдента для уровня значимости α и число степеней свободы п-2; – стандартное отклонение свободного члена и коэффициента регрессии соответственно; п – число наблюдений.