ЕН 01 МАТЕМАТИКА
Сборник заданий для внеаудиторной самостоятельной работы по теме: «Применение определённого интеграла для решения физических задач».
для специальности:
100126 Сервис домашнего и коммунального хозяйства
Вологда 2013
Математика: Сборник заданий для внеаудиторной самостоятельной работы по теме: «Применение определённого интеграла для решения физических задач» для специальности: 100126 Сервис домашнего и коммунального хозяйства
Данный сборник заданий для внеаудиторной самостоятельной работы по теме: «Применение определённого интеграла для решения физических задач» представляет собой учебно-методическое пособие по организации самостоятельной внеаудиторной работы студентов.
Содержит задания для самостоятельной внеаудиторной работы для шести вариантов и критерии оценки выполнения самостоятельной работы.
Комплект призван помочь студентам систематизировать и закрепить полученные на аудиторных занятиях по математике теоретический материал, сформировать практические навыки.
Составитель: Е. А. Севалёва – преподаватель математики высшей категории БОУ СПО ВО «Вологодский строительный колледж»
Содержание.
1. Пояснительная записка.
2. Самостоятельная работа.
3. Критерии оценки.
4. Литература.
Пояснительная записка
Данная работа представляет собой учебно-методическое пособие по организации самостоятельной внеаудиторной работы студентов по дисциплине ЕН 01 «Математика» для специальности 100126 Сервис домашнего и коммунального хозяйства.
Цель методических указаний состоит в обеспечении эффективности самостоятельной работы, определении ее содержания, установления требований к оформлению и результатам самостоятельной работы.
Целями самостоятельной работы студентов по дисциплине ЕН 01 «Математика» являются:
· систематизации и закрепления полученных теоретических знаний и практических навыков;
· углубление и расширение теоретических знаний;
· формирование умений использовать справочную и дополнительную литературу;
· развитие познавательных способностей и активности студентов, творческой инициативы, самостоятельности и самоорганизации;
· активизации учебно-познавательной деятельности будущих специалистов.
Самостоятельные работы выполняются индивидуально в свободное от занятий время.
Студент обязан:
- перед выполнением самостоятельной работы, повторить теоретический материал, пройденный на аудиторных занятиях;
- выполнить работу согласно заданию;
- по каждой самостоятельной работе представить преподавателю отчет в виде письменной работы.
Самостоятельная работа по теме:
«Применение определённого интеграла для решения физических задач»
Цель: научиться применять определённый интеграл для решения физических задач.
Теория.
Вычисление пути, пройденного точкой.
Путь, пройденный точкой при неравномерном движении по прямой с переменной скоростью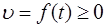 
а промежуток времени от 
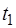до 
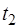, вычисляется по формуле
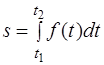…… (1)
Пример 1. Скорость движения точки изменяется по закону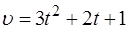 
м/с. Найти путь, пройденный точкой за 10 с от начала движения.
Решение: Согласно условию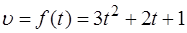 
, 
, 
.
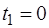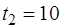По формуле (1) находим:
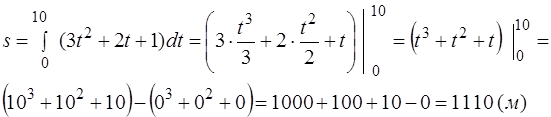
Ответ: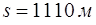 
.
Пример 2. Скорость движения точки изменяется по закону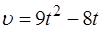 
м/с. Найти путь, пройденный точкой за 4-ую секунду.
Решение: Согласно условию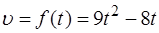 
, 
, 
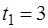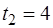
Следовательно:
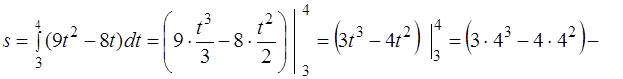
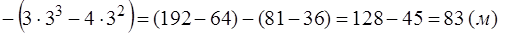
Ответ: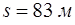 
.
Пример 3. Скорость движения точки изменяется по закону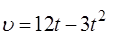 
м/с. Найти путь, пройденный точкой от начала движения до её остановки.
Решение:
· Скорость точки равна 0 в момент начала движения и в момент остановки.
· Определим, в какой момент времени точка остановится, для этого решим уравнение: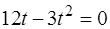 
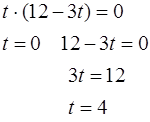
То есть , .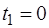
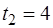· По формуле (1) находим:
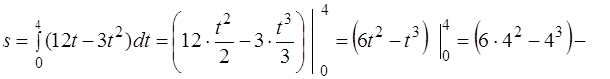
Ответ: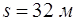 
.
Вычисление работы силы.
Работа, произведённая переменной силой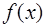 
при перемещении по оси Ох материальной точки от х = а до х = 
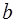, находится по формуле:
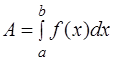…… (2)
При решении задач на вычисление работы силы часто используется закон Гука: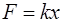 
……(3), где
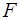- сила (Н);
х – абсолютное удлинение (сжатие) пружины, вызванное силой 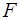(м);
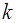- коэффициент пропорциональности (Н/м).
Пример 4. Вычислить работу силы 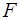при сжатии пружины на 0,04 м, если для сжатия её на 0,01 м нужна сила 10 Н.
Решение:
· Так как х = 0,01 м при силе 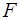=10 Н, то, подставляя эти значения в равенство (3): 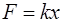, получим:
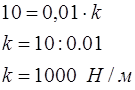
· Подставив теперь в это же равенство найденное значение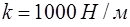 
, находим 
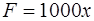, т.е. 
.
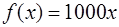· Искомую работу найдём по формуле (2):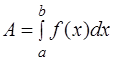
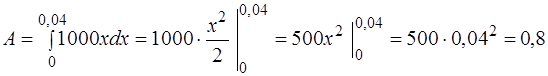Дж.
Ответ: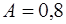 
Дж.
Пример 5. Пружина в спокойном состоянии имеет длину 0,2 м. Сила в 50 Н растягивает пружину на 0,01 м. Какую работу надо совершить, чтобы растянуть пружину от 0,22 м до 0,32 м?
Решение:
· Так как х = 0,01 при силе 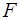=50 Н, то, подставляя эти значения в равенство (3): 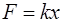, получим:
· Подставив теперь в это же равенство найденное значение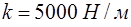 
, находим 
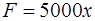, т.е. 
.
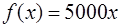· Находим пределы интегрирования: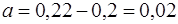 
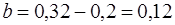м, 
м.
· Искомую работу найдём по формуле (2):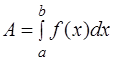
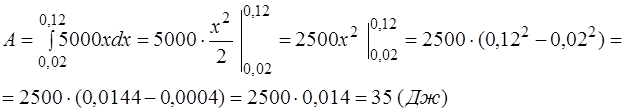
Ответ: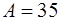 
Дж.
Пример 6. При сжатии пружины на 0,05 м затрачивается работа 25 Дж. Какую работу необходимо совершить, чтобы сжать пружину на 0,1 м?
Решение:
· Зная величину сжатия пружины 0,05 м и произведённую при этом работу 25 Дж, воспользуемся формулой (2):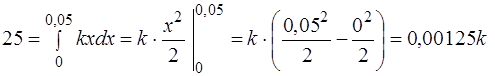 
.
· Вычислим значение :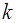 
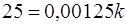
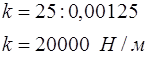
· Теперь по этой же формуле (2) находим необходимую работу:
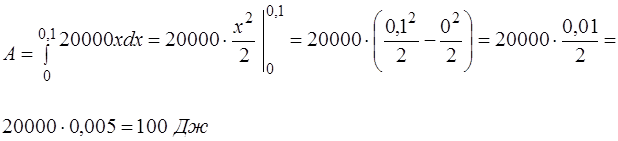
Ответ: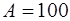 
Дж.
Пример 7. Для растяжения пружины на 0,04 м необходимо совершить работу 20 Дж. На какую длину можно растянуть пружину, совершив работу 80 Дж?
Решение:
· Зная величину растяжения пружины 0,04 м и произведённую при этом работу 20 Дж, воспользуемся формулой (2):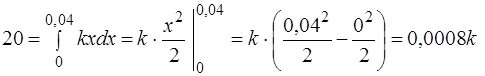 
.
· Вычислим значение :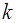 
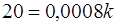
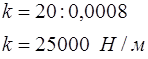
· Пусть х1 – величина растяжения пружины, соответствующая произведённой при этом работе в 80 Дж. Тогда:
.
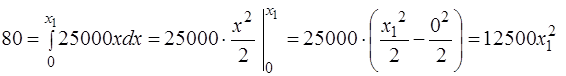· Решим полученное уравнение: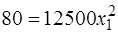 
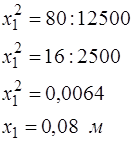
Ответ: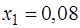 
м.
