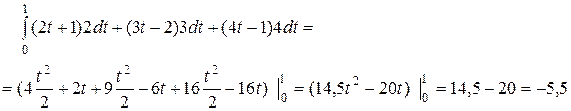Рассмотрим пространство R 2. Пусть в области D Ì R 2 определены две непрерывные функции P (x,y), Q (x,y), тогда в любой точке М(x, y) Î D определена векторная функция `F(x, y) = (P (x, y); Q (x, y)), которую в векторной форме можно записать в виде: 
.
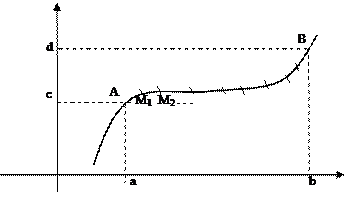
Пусть функции P (x, y) и Q (x, y) определены в точках гладкой дуги 
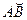кривой L Ì D. Разобьем дугу на части точками М1,М2,...М n. На каждой дуге 
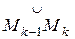возьмем произвольную точку 
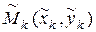и вычислим значение 
.
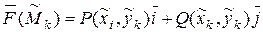Пусть [ a, b ]и[ c, d ] – проекции 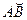на OX и OY соответственно, т.е. x Î[ a, b ], y Î [ c, d ], когда М(х, у) Î 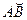. Каждую частичную дугу спроектируем на оси координат, получим разбиение отрезков [ a, b ]и[ c, d ] на n частей, длины частичных интервалов обозначим соответственно D хk и D yk. Составим интегральную сумму вида:
.
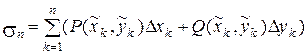Эта сумма представляет собой сумму скалярных произведений векторов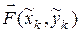 
на векторы 
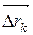, где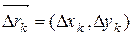 
, т.е. 
Обозначим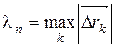 
Определение 5.1
Если существует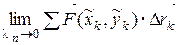 
, не зависящий ни от способа разбиения дуги 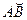на части, ни от выбора точки 
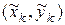, то этот предел называется криволинейным интегралом II рода и обозначается 
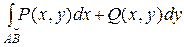или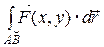 
.
Итак, криволинейный интеграл II рода
,
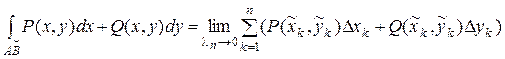Заметим, что условие 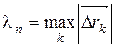→0 равносильно условиям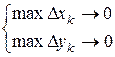 
В отличие от криволинейного интеграла I рода, который еще называют интегралом по длине дуги, криволинейный интеграл II рода называют криволинейным интегралом по координатам.
Свойства:
1. 
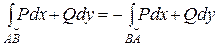- меняет знак при изменении ориентации кривой (направления движения по кривой).
2. Свойство линейности, аддитивности (АВ = АС + СВ) аналогичны свойствам криволинейного интеграла I рода. В частности,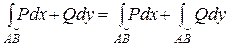 
3. Связь между криволинейными интегралами I и II рода выражает формула: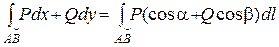 
,
где (cosa,cosb) – направляющие косинусы касательной к дуге АВ в любой ее точке.
Способы вычисления криволинейного интеграла II рода:
1) Если АВ: y = j(x), x Î [ a, b ], то dy = j¢(x) dx и
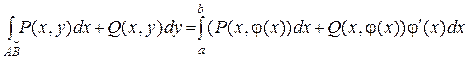
2) Если АВ: x = y(y), y Î [ c, d ],то dx = y¢(y) dy и
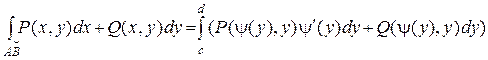
3) Если АВ: 
, t Î [a,b], dx = x ¢(t) dt, dy = y ¢(t) dt, то
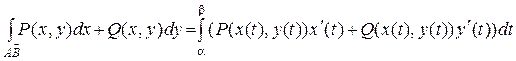
Аналогично можно дать определение криволинейного интеграла II рода по пространственной кривой
Пример 2.
Вычислить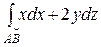 
, где АВ – отрезок прямой между точками В(1, 1, 1), А(0, 0, 2).
Решение: Найдем уравнение АВ:
.
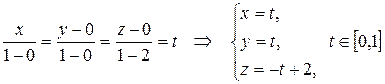Тогда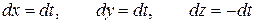 
, значит,
.
Физический смысл криволинейного интеграла II рода:
определяет работу силы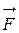 
при перемещении материальной точки вдоль кривой L из положения А в положение В. Действительно, пусть материальная точка M(x, y) движется вдоль некоторой плоской (можно аналогично рассмотреть и пространственную) кривой L от точки A к точке B. Пусть вдоль кривой действует сила 
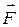, которая меняется по величине и направлению при перемещении точки M, т.е. сила 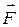является функцией точки: 
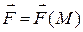. Найдём работу A силы при перемещении точки из положения A в положение B.
Как известно, в случае, когда сила постоянна, а путь прямолинейный, работа равна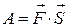 
(*), т.е. скалярному произведению вектора силы 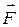на вектор перемещения 
. Воспользуемся этим фактом и для решения поставленной задачи.
1) Разобьём дугу AB в направлении от точки A к точке B на n частей точками A=M 0,M1, M2,…, Mn=B и обозначим через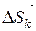 
вектор 
. Тогда
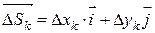
(рис.34). Пусть λ – наибольшая из длин этих векторов, т.е.
.
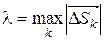2) На каждой элементарной дуге выберем произвольную точку 
k(xk,yk) и предположим, что в пределах каждой элементарной дуги сила 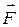постоянна и равна 
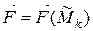. Тогда в силу (*), скалярное произведение 
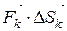можно рассматривать как приближённое значение работы Ak силы вдоль дуги 
.
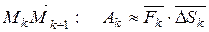Пусть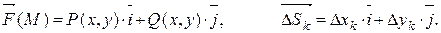 
Тогда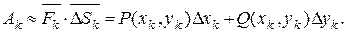 
3) Искомая работа A силы на всей дуге AB будет приближённо равна
и это приближённое равенство тем точнее, чем меньше λ.
4) Следовательно, истинное значение работы A силы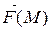 
при перемещении точки M по дуге AB получим, переходя к пределу при λ→0: 
= 
.
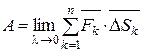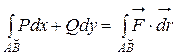Рассмотрим замкнутую кривую C, будем называть ее замкнутымконтуром. Ориентацию на этой кривой выберем следующим образом: если при движении точки М вдоль кривой ограниченная этим контуром область G остается слева, то направление движения (ориентацию на кривой) будем считать положительным. В противном случае – отрицательным.
 | |||
 | |||
Криволинейный интеграл II рода по замкнутому контуру будем обозначать 
Справедлива
Теорема 5. 1 (формула Грина)
Пусть С – положительно ориентированная замкнутая кривая, ограничивающая область D, а функции P(x, y) и Q(x, y) непрерывны вместе со своими производными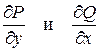 
в области D и на границе C. Тогда имеет место равенство
.
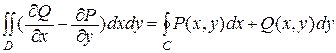(без доказательства). Это равенство называют формулой Грина.
Пример 3.
Вычислить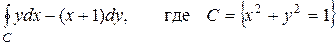 
.
Решение: Здесь Р(х, у) = у, Q(x, y) =(x +1),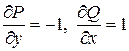 
. Тогда по формуле Грина
.
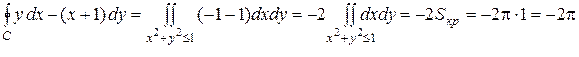Здесь мы используем свойство двойного интеграла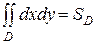 
Заметим, что если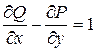 
, то
Рассмотрим три случая:
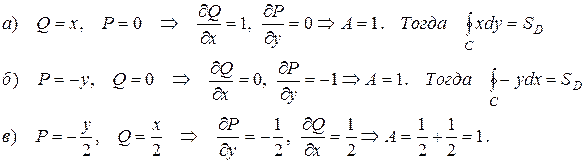
Тогда
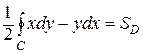
Таким образом, с помощью криволинейного интеграла II рода по замкнутому контуру С можно найти площадь области, ограниченной этим контуром:
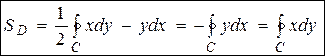
Справедливо также следующая важная
Теорема 5.2
Если функции P(x, y) и Q(x, y) непрерывны вместе со своими производными 
в области D и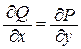 
, то следующие утверждения эквивалентны:
1. для любого замкнутого контура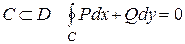 
;
2. 
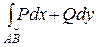- не зависит от пути интегрирования АВ, а зависит только от начальной А и конечной В его точек и обозначается: 
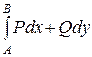. Условие 
при этом называют условием независимости криволинейного интеграла от пути интегрирования.
3. существует функция и (х, у) такая, что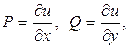 
а 
и тогда
.
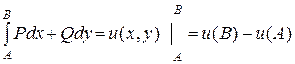Доказательство первого из этих утверждений легко следует из формулы Грина. Доказательство второго из этих утверждений проведите или изучите самостоятельно.
Третье утверждение рассмотрим без доказательства. Отметим только его важный смысл: равенство 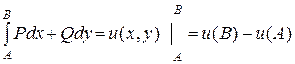, по существу, представляет аналог формулы Ньютона-Лейбница для криволинейного интеграла второго рода. Если при этом А (х 0, y 0) – некоторая фиксированная точка, а В (x, y) – текущая точка области D, то
,
что означает аналог теоремы Барроу, где С = - u (х 0, y 0). Таким образом, если по известному дифференциалу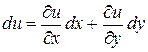 
функции двух переменных требуется найти функцию u (х, y), нужно вычислить криволинейный интеграл второго рода от выражения du по любому пути, соединяющему произвольную фиксированную точку (х 0, у 0) области определения функций 
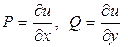и текущую точку (х, у). Очевидно, такие функции определяются с точностью до константы.
Пример 4.
Вычислить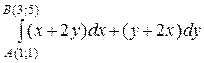 
Так как P = x+ 2 y, Q = y+ 2 x – непрерывные функции, 
– тоже непрерывные и выполняется условие , то интеграл не зависит от вида кривой, а зависит только от точек (1, 1) и (3, 5). Значит, можно выбрать любую линию, их соединяющую.
Рассмотрим ломанную АСВ, где С (3, 1), со звеньями, параллельными осям координат. Тогда 
Но АС: y = 1, dy = 0, x Î [1, 3],
CB: x = 3, dx = 0, y Î [1, 5].
Тогда
Рассмотрим прямую АВ: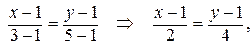 
2(x -1) = (y -1), откуда
y = 2 x- 2+1, y = 2 x -1, а dy = 2 dx. Тогда
.
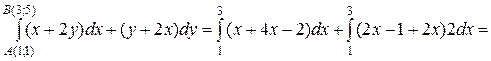
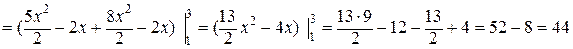Пример 5.
Найти функцию U(x,y) по ее дифференциалу
dU = (x 4 + 4 xy 3) dx + (6 x 3 y 2 - 5 y 4) dy.
Решение: Убедимся в том, что для P=x 4+4 xy 3 и Q =6 x 3 y 2-5 y 4 выполняется условие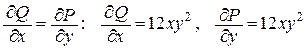 
.
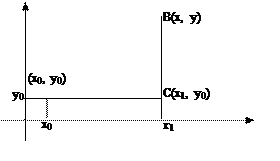Тогда 
= 
,
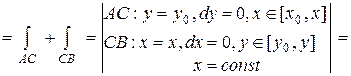
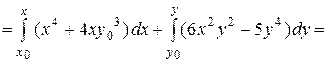
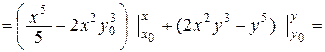
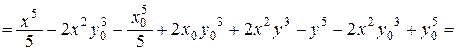
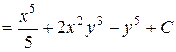где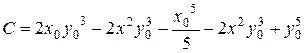 
.
Если взять (х 0, y 0)= (0, 0), получим:
.
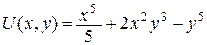В случае функции 3-х переменных и пространственной кривой L, условия независимости интеграла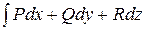 
от пути интегрирования (или того, что 
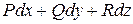есть дифференциал некоторой функции) имеют вид:
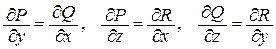
Пример 6.
Вычислить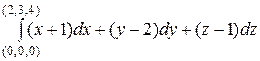 
.
Решение: Здесь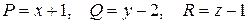 
, 
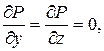
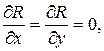
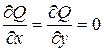, значит, данный криволинейный интеграл не зависит от пути интегрирования, в только от начальной (0, 0, 0) и конечной (2, 3, 4) точек. Возьмем, например отрезок прямой, соединяющей эти точки, его уравнения
.
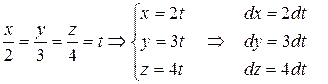Тогда
