Вычисление двойного интеграла

Лекция 22. Двойной интеграл, его вычисление. Криволинейные интегралы.

Ч).

Содержание лекции: Двойной интеграл, его вычисление по правильной области в декартовых координатах. Криволинейный интеграл первого рода, его вычисление.

Криволинейный интеграл второго рода.

 

Двойной интеграл

 

Пусть в ограниченной замкнутой области DÌ R ² задана непрерывная функция .

Разобьем D на n частей D _i, площадь D _i обозначим DS _i, а

l _n = .

В каждой области D _i произвольным образом возьмем точку ÎD _i и вычислим f (P_i). Составим – интегральную сумму для функции по области D. Будем рассматривать последовательность {s _n } интегральных сумм, соответствующую различным разбиениям таким, что l _n ® 0 при n ® ¥ (нормальная последовательность разбиений).

Определение 22. 1.

Если существует конечный предел последовательности {s _n } при l_n ® 0, не зависящий ни от способа разбиения области D, ни от выбора точек , то этот предел называется двойным интегралом по области D от функции f (х, у) и обозначается .

Таким образом, по определению:

В этом случае функция называется интегрируемой в области D.

 

Теорема 4.1.

Если f (P) непрерывна в D, то она интегрируема в этой области (то есть существует ).

Свойства двойного интеграла:

1.

2. 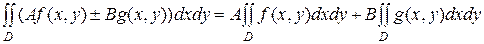- свойство линейности

3. Если , то

(свойство аддитивности)

4. Если " P (x, y)ÎD, то .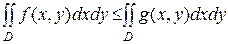

5. Если m £ f ((x, y) £ M, " P (x, y)ÎD,то .

6. Существует точка Q (x, y)Î D: 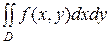= f(Q) ×|D| (Теорема о среднем.)

(4-6 – свойства оценки интеграла по области).

Рассмотрим геометрический смысл интеграла

Введем понятие: цилиндрическим телом назовем пространственное (в R ³) тело, ограниченное плоскостью z= 0, поверхностью и цилиндрической поверхностью, направляющая которой есть граница области D Î R ³, а образующая параллельна оси OZ.

Разобьем область D на части D _{ij ,} и на каждой из них построим параллелепипед с высотой f (ξ_i, η_j), где Р (ξ_i, η_j) – любая точка, принадлежащая D_{ij .}

Тогда

V_{ц.т .} ,

откуда

V_{ц.т .} = .

Таким образом, двойной интеграл, с геометрической точки зрения, численно равен объему цилиндрического тела. Физическую интерпретацию (масса плоской области) дать самостоятельно.

Вычисление двойного интеграла

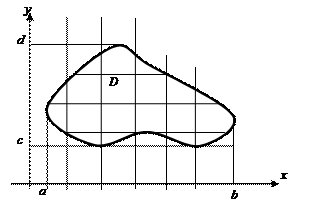Так как по определению интеграл не зависит от способа разбиения D на части, то разобьем D на части прямыми, параллельными осям координат. Для этого спроектируем D на оси координат. Получим отрезки [ a, b ] на оси ОХ и [ c, d ] на OY соответственно.

Разобьем эти отрезки точками:

a < x ₁ < x ₂ <... < x_n = b

c < y ₁ < y ₂ <... < y_k = d

Тогда область D разобьется на прямоугольники (полные, или их части) D_ij, i= , j = , площади которых:

| D_ij | = D S_ij = D x_i D y_j, гдеD x_i = x_i- x_{i- 1},D y_j = y_j - y_{j- 1}

И если , то по определению:

,

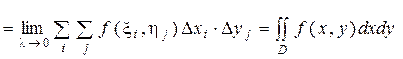где (ξ_i, η_j) - любая точка, принадлежащая прямоугольнику D_ij.

Но так как

,

то есть имеем двойное суммирование, отсюда и термин (и обозначение) – двойной интеграл.

 

 

Определим способы вычисления ДИ

Определение 22.2.

Область D Î R² называется правильной в направлении оси OY, если она ограниченна линиями x = a, x = b, y = j₁(x), y = j₂(x), причем j₁(x) £ j₂(x) для любого x Î[ a,b ].

В этом случае каждая прямая, проходящая параллельно OY через любую внутреннюю точку PÎD, пересекает границу области только в двух точках М₁, М₂. Точку М₁ называют точкой «входа» (в направлении OY), М₂ – точкой «выхода». Линия y = j₁(x), на которой лежат точки «входа» - это «линия входа», y= j₂(x) – «линия выхода».

Таким образом, область правильная в направлении оси, если она в направлении этой оси имеет только одну линию входа и одну линию выхода.

Например, на рисунке изображена область, неправильная в направлении оси ОХ, ее можно разбить на две правильные области:

 

 

Аналогично определяется область, правильная в направлении оси ОХ: ограниченную линиями y = c, y = d, кривыми х = y₁(у), х = y₂ (у), причем y₁(у) £ y₂(у) для любого y Î[ c,d ].

 

Теорема 22.2.

Пусть f (x,y) – непрерывная в области D функция.

1) Если D – правильная в направлении оси OY, то

2) Если D – правильная в направлении оси OX, то

Интегралы, стоящие справа, называются повторными интегралами (или двукратными). Последняя запись – условное, сокращенное изображение предыдущей. Понимается она так, как записано в центре. При этом первый (левый) интеграл называется внешним, а его переменная – внешней переменной, пределы – внешними пределами.

Второй (в скобках или справа) – внутренний интеграл, его переменная – внутренняя, пределы – внутренние. Запись этих интегралов определяет порядок интегрирования: no dx - no dy; no dy - no dx (так же как при вычислении смешанной производной второго порядка).

Пример 1.

D – правильная в любом направлении.

 

 

 

Пример 2.

(точки пересечения: х + х = 2, х = 1, y = 1)

=