Параметрические уравнения прямой l в пространстве:
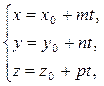 (15)
(15)
где 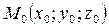 – фиксированная точка прямой;
– фиксированная точка прямой;
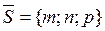 – направляющий вектор прямой l, т.е. любой вектор, параллельный l;
– направляющий вектор прямой l, т.е. любой вектор, параллельный l;
t – числовой параметр.
Каждому значению параметра 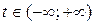 соответствует единственная точка прямой l.
соответствует единственная точка прямой l.
Канонические уравнения прямой:
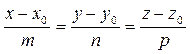 . (16)
. (16)
Уравнения прямой, проходящей через две данные точки 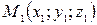 и
и 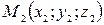 :
:
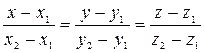 . (17)
. (17)
Углом 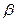 между прямыми называют угол между их направляющими векторами
между прямыми называют угол между их направляющими векторами 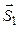 ={ m 1; n 1; p 1} и
={ m 1; n 1; p 1} и 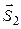 ={ m 2; n 2; p 2}, или дополнительный к нему (обычно берется острый угол), то есть
={ m 2; n 2; p 2}, или дополнительный к нему (обычно берется острый угол), то есть
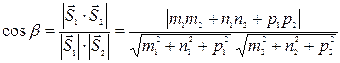 . (18)
. (18)
Углом между плоскостью и прямой l (в случае их пересечения) называется угол между прямой и её проекцией на плоскость. Синус угла 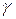 между плоскостью
между плоскостью  и прямой
и прямой 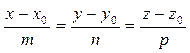 определяется по формуле:
определяется по формуле:
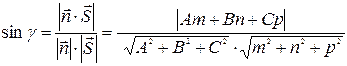 . (19)
. (19)
Примерный вариант и образец выполнения
РГЗ №1
Задача 1. Даны координаты вершин треугольника АВС:
А (–3; –1), В (4; 6), С (8; –2).
Требуется: 1) вычислить длину стороны ВС;
2) составить уравнение стороны ВС;
3) найти внутренний угол треугольника при вершине В;
4) составить уравнение высоты АК, проведенной из вершины А;
5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан);
6) сделать чертеж в системе координат.
Задача 2. Даны координаты точек – вершин пирамиды ABCD:
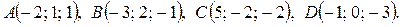
Требуется:
1) вычислить длину ребра AB;
2) найти уравнение плоскости грани ABC;
3) найти угол  между гранями ABC и BCD;
между гранями ABC и BCD;
4) составить параметрические уравнения прямой AB;
5) составить канонические уравнения высоты пирамиды DK, проведенной из вершины D;
6) найти координаты точки пересечения DK и грани ABC;
7) найти угол  между ребрами AB и BC;
между ребрами AB и BC;
8) найти угол 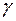 между ребром AD и гранью ABC;
между ребром AD и гранью ABC;
9) сделать чертеж пирамиды в системе координат.
Решение задачи 1.
1) Вычислим длину стороны ВС по формуле (1):
| BС |= 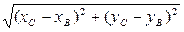 =
= 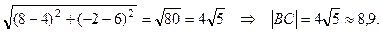
2) Составим уравнение стороны ВС, используя формулу (8):
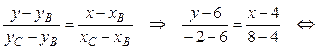
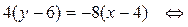
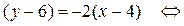 y = –2 x + 14 – уравнение ВС.
y = –2 x + 14 – уравнение ВС.
3) Внутренний угол треугольника при вершине В найдем как угол между прямыми ВА и ВС. Для этого сначала вычислим угловой коэффициент прямой ВА по формуле (7):
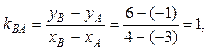
и возьмем из уравнения ВС угловой коэффициент прямой ВС: 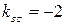 .
.
Из расположения точек A, B, C на координатной плоскости видно, что угол В в треугольнике ABC – острый, поэтому по формуле (11) вычислим
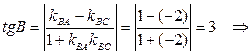
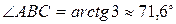 .
.
4) Для получения уравнения высоты АK, проведенной из вершины А, используем уравнение пучка прямых (6) и условие перпендикулярности прямых (10). Сначала вычислим угловой коэффициент прямой АK. Так как 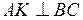 , то
, то 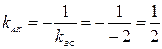 .
.
Уравнение AK получим по формуле (6):
у – уА = kAK (x – x A) 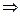 у – (–1) =
у – (–1) = 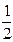 (x – (–3))
(x – (–3)) 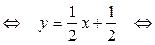
x –2 y + 1 = 0 – уравнение AK.
5) Для определения координат центра тяжести треугольника используем свойство точки пересечения его медиан: если AМ – медиана треугольника и P – точка пересечения его медиан, то P делит AМ в отношении 2: 1, начиная от точки А, т.е. 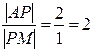 .
.
Основание медианы AМ – точка М является серединой отрезка ВС. Найдем координаты точки М по формулам (3):
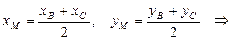
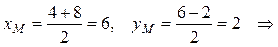 М (6; 2).
М (6; 2).
Теперь, когда координаты концов отрезка AМ известны, найдем координаты точки P, которая делит AМ в отношении 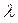 = 2, начиная от точки А, по формулам деления отрезка в заданном отношении (2):
= 2, начиная от точки А, по формулам деления отрезка в заданном отношении (2):
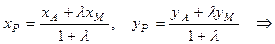
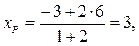
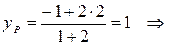
P (3; 1) – центр тяжести треугольника АВС.
6) Построим чертеж к задаче в системе координат ХОY (рис. 3). Полученные при решении задачи результаты не противоречат чертежу.
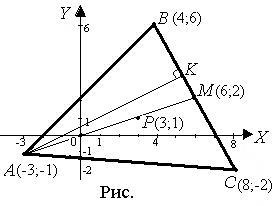
Ответы:
1) длина стороны | BС | = 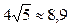 ;
;
2) уравнение стороны ВС: y = –2 x + 14;
3) угол при вершине В: 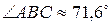 ;
;
4) уравнение высоты АK: x –2 y + 1 = 0;
5) координаты центра тяжести треугольника P (3; 1);
6) чертеж на рис. 3.
Решение задачи 2.
1) Длину ребра 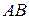 найдем по формуле:
найдем по формуле:
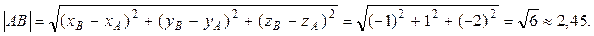
2) Чтобы получить уравнение плоскости грани ABC, необходимо найти вектор, перпендикулярный плоскости ABC, т.е. вектор, перпендикулярный векторам 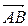 и
и 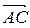 . Одним из таких векторов является векторное произведение
. Одним из таких векторов является векторное произведение 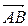 на
на 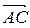 . Для того, чтобы найти его, сначала вычислим координаты векторов по формулам:
. Для того, чтобы найти его, сначала вычислим координаты векторов по формулам:
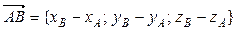 ={–3–(–2); 2–1; –1–1} = {–1; 1; –2},
={–3–(–2); 2–1; –1–1} = {–1; 1; –2},
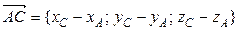 ={7; –3; –3}.
={7; –3; –3}.
Найдем векторное произведение 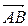 и
и 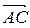 :
:
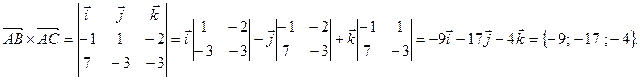 В качестве вектора нормали к плоскости ABC можно взять любой вектор, коллинеарный полученному, например,
В качестве вектора нормали к плоскости ABC можно взять любой вектор, коллинеарный полученному, например, 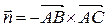 = {9; 17; 4}. Используем уравнение плоскости, проходящей через точку
= {9; 17; 4}. Используем уравнение плоскости, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору 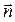 (формула (12):
(формула (12): 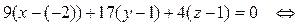
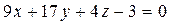 – уравнение плоскости грани ABC.
– уравнение плоскости грани ABC.
3) Прежде, чем найти угол  между гранями ABC и BCD, получим уравнение грани BCD, используя уравнение плоскости, проходящей через три заданные точки
между гранями ABC и BCD, получим уравнение грани BCD, используя уравнение плоскости, проходящей через три заданные точки 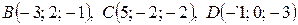 (формула (13):
(формула (13):
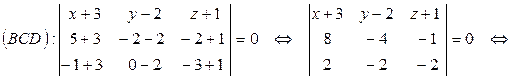
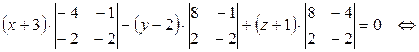
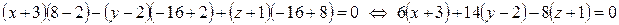
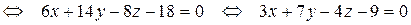 – уравнение грани BCD.
– уравнение грани BCD.
Из уравнения плоскости BCD возьмем координаты вектора нормали 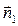 , перпендикулярного этой плоскости:
, перпендикулярного этой плоскости: 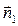 ={3; 7; –4}.
={3; 7; –4}.
Косинус угла  между плоскостями (гранями) ABC и BCD найдем по формуле(14):
между плоскостями (гранями) ABC и BCD найдем по формуле(14):
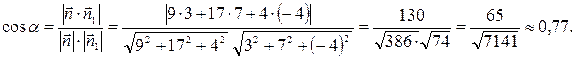
Отсюда 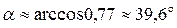 .
.
4) Уравнения ребра AB можно записать как параметрические уравнения прямой, проходящей через точку A (–2;1;1) и имеющей направляющий вектор 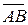 = {–1; 1; –2} (формулы (15)):
= {–1; 1; –2} (формулы (15)):
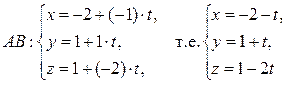 – параметрические уравнения AB.
– параметрические уравнения AB.
Другой способ: можно использовать уравнения прямой, проходящей через две точки 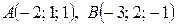 (формулы (17)):
(формулы (17)):
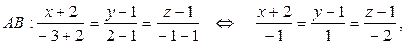
откуда, обозначив каждую из дробей буквой t, получаем:
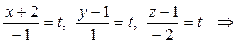
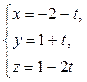 – параметрические уравнения AB.
– параметрические уравнения AB.
5) Высота пирамиды DK – это прямая, проведенная из вершины D перпендикулярно грани ABC. Она имеет направляющий вектор 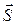 , коллинеарный вектору нормали плоскости ABC. Можно взять, например,
, коллинеарный вектору нормали плоскости ABC. Можно взять, например, 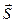 =
= 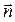 = {9; 17; 4}. Запишем канонические уравнения высоты DK, используя точку D (–1; 0; –3) и вектор
= {9; 17; 4}. Запишем канонические уравнения высоты DK, используя точку D (–1; 0; –3) и вектор 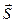 ={9; 17; 4} (формулы (16)):
={9; 17; 4} (формулы (16)):
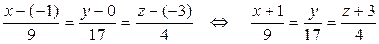 – канонические уравнения DK.
– канонические уравнения DK.
6) Прежде, чем найти точку пересечения DK и грани ABC, получим параметрические уравнения прямой DK. Обозначив каждую из дробей в канонических уравнениях буквой t, получаем:
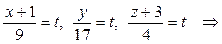
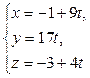 – параметрические уравнения DK.
– параметрические уравнения DK.
Точка пересечения DK и грани ABC (точка К) лежит на прямой, а значит, имеет координаты 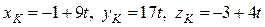 , и принадлежит плоскости, т.е. ее координаты удовлетворяют уравнению плоскости ABC. Поэтому координаты точки K найдем, решив систему:
, и принадлежит плоскости, т.е. ее координаты удовлетворяют уравнению плоскости ABC. Поэтому координаты точки K найдем, решив систему:
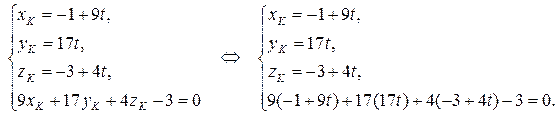
Решим последнее уравнение относительно t:
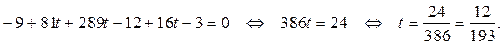
Вычислим координаты точки K, подставив найденное значениепараметра t в первые три уравнения системы:
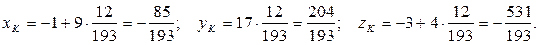

Итак, точка пересечения DK и грани ABC: 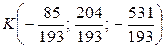 .
.
7) Угол 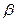 между ребрами AB и BC найдем, как угол между направляющими векторами прямых AB и BC:
между ребрами AB и BC найдем, как угол между направляющими векторами прямых AB и BC: 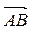 = {–1; 1; –2} и
= {–1; 1; –2} и 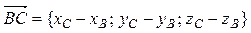 ={8; –4; –1}. Вычислим косинус угла
={8; –4; –1}. Вычислим косинус угла 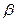 по формуле (18):
по формуле (18):
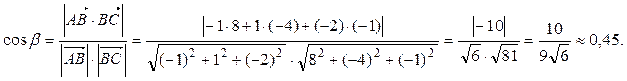
Тогда угол между ребрами AB и BC: 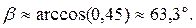
8) Чтобы определить угол 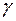 между ребром AD и гранью ABC, найдем направляющий вектор прямой:
между ребром AD и гранью ABC, найдем направляющий вектор прямой: 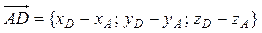 ={1; –1; –4}. Плоскость ABC имеет вектор нормали
={1; –1; –4}. Плоскость ABC имеет вектор нормали 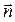 = {9; 17; 4}. Синус угла
= {9; 17; 4}. Синус угла 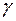 между прямой
между прямой 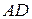 и плоскостью ABC можно вычислить по формуле (19):
и плоскостью ABC можно вычислить по формуле (19):
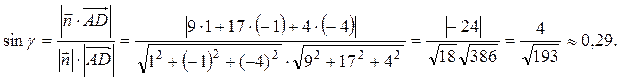
Тогда угол между ребром AD и гранью ABC: 
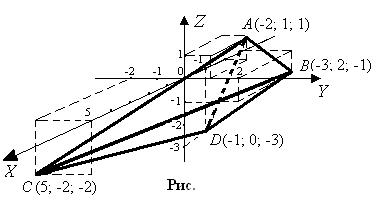
9) Выполним чертеж пирамиды в системе координат (рис.4).
Ответы:
1) 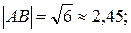
2) АВС: 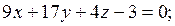
3) 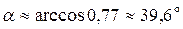 ;
;
4) 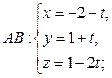
5) DK: 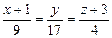 ; 6)
; 6) 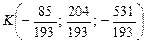 ;
;
7) 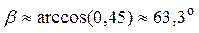 ; 8)
; 8) 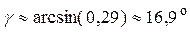 ;
;
9) чертеж пирамиды на рис. 4.






