Оглавление
Варианты контрольной работы №2………………………………………………….2
Справочный материал по теме«Аналитическая геометрия на плоскости……….3
1. Декартова система координат (ДСК) на плоскости………………….……....3
2. Прямая линия на плоскости……………………………………………………3
Справочный материал по теме «Аналитическая геометрия в пространстве»……4
1. Уравнение плоскости в пространстве…………………………….……..........4
2. Уравнения прямой в пространстве…………………………………..………..5
Примерный вариант и образец выполнения домашней контрольной №2………...6
Варианты контрольной работы №2
Задача 1. Даны координаты вершин треугольника АВС.
| № варианта | Координаты точек | № варианта | Координаты точек |
| А (–2; –3), В (2; 7), С (6; –1) | А (3; –3), В (–4; 1), С (–2; 5) | ||
| А (–5; 1), В (6; 3), С (–4; –7) | А (3; 5), В (–2; 2), С (2; –4) | ||
| А (4; 5), В (–3; 2), С (5; –4) | А (–2; 4), В (5; 6), С (3; –4) | ||
| А (7; –7), В (1; 2), С (–5; –4) | А (3; 7), В (–4; 1), С (–2; –5) | ||
| А (–2; –3), В (6; 3), С (5; –4) | А (3; 5), В (5; 6), С (3; –4) | ||
| А (–3; 4), В (4; 5), С (8; –3) | А (4; 3), В (–3; –2), С (–7; 2) |
Требуется:
1) вычислить длину стороны ВС;
2) составить уравнение стороны ВС;
3) найти внутренний угол треугольника при вершине В;
4) составить уравнение высоты АК, проведенной из вершины А;
5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан);
6) сделать чертеж в системе координат.
Задача 2. Даны координаты точек – вершин пирамиды ABCD.
| № варианта | Координаты точек |
| А (1; 2; –1), В (0; 0; 1), С (1; –3; 3), D (2; –1; –1) | |
| А (7; 2; 4), В (7; –1; –2), С (3; 3; 1), D (4; 2; 1) | |
| А (1; 3; 6), В (2; 2; 1), С (–1; 0; 1), D (–4; 6; –3) | |
| А (–2; 0; –4), В (–1; 7; 1), С (4; –8; –4), D (1; –4; 6) | |
| А (1; 2; 0), В (3; 0; –1), С (5; –2; 3), D (3; 2; –1) | |
| А (–1; 1; 2), В (2; 1; –2), С (–2; 0; 4), D (2; –1; 2) | |
| А (4; 2; 5), В (2; –3; 0), С (–10; 5; 8), D (–5; 2; 4) | |
| А (2; –1; 1), В (–1; –3; 2), С (–2; 3; 1), D (–1; 2; –3) | |
| А (7; 2; 4), В (2; 2; 1), С (4; –8; –4), D (3; 2; –1) | |
| А (–1; 1; 2), В (2; –3; 0), С (–10; 5; 8), D (–2; 1; –1) | |
| А (–1; 1; 2), В (–2; 0; 3), С (3; 6; –3), D (–1; –2; 7) | |
| А (4; –1; 3), В (–2; 1; 0), С (0; –5; 1), D (–2; 1; –1) |
Требуется:
1) вычислить длину ребра AB;
2) найти уравнение плоскости грани ABC;
3) найти угол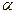 
между гранями ABC и BCD;
4) составить параметрические уравнения прямой AB;
5) составить канонические уравнения высоты пирамиды DK, проведенной из вершины D;
6) найти координаты точки пересечения DK и грани ABC;
7) найти угол 
между ребрами AB и BC;
8) найти угол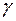 
между ребром AD и гранью ABC;
9) сделать чертеж пирамиды в системе координат.
Справочный материал по теме «Аналитическая геометрия на плоскости» (задачА 1)
Декартова система координат (ДСК) на плоскости
Расстояние |АВ| между двумя точками А (хА; уА)и В (хВ; уВ) (рис.1):
| AB | =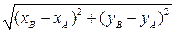 
. (1)
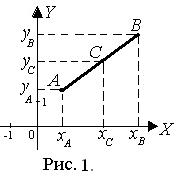Деление отрезка в заданном отношении. Если точка С делит отрезок АВ в отношении λ, начиная от точки A (рис. 1), т.е. 
, то координаты точки C:
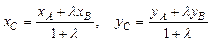. (2)
Если точка С делит отрезок АВ пополам, т.е. 
=1, то координаты точки C:
. (3)
В ДСК уравнение линии имеет вид F (х, у) = 0 или у = f (х).
Прямая линия на плоскости
Общее уравнение прямой на плоскости:
Ах + В у + С = 0.
Уравнение прямой с угловым коэффициентом (рис. 3):
у = kx+ b. (4)
Уравнение вертикальной прямой (рис. 2):
х = а. (5)
Уравнения прямых, проходящих через одну заданную точку М (х 0; у 0) (уравнение пучка прямых):
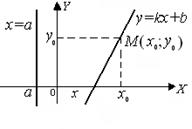у – y 0 = k (x – x 0). (6)
Угловой коэффициент прямой, проходящей через две заданные точки А (х 1; у 1) и В (х 2; у 2):
Рис.2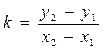 
. (7)
Уравнение прямой, проходящей через две заданные точки:
. (8)
Пусть на плоскости заданы две прямые, которым соответствуют уравнения с угловыми коэффициентами: у = k 1 x + b 1 и у = k 2 x + b 2.
Условие параллельности прямых на плоскости:
k 1 = k 2.. (9)
Условие перпендикулярности прямых:
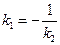. (10)
Если одна из двух перпендикулярных прямых вертикальная, т.е. k 2 не существует, то k 1 = 0 и обратно: если k 2 = 0, то k 1 не существует.
Тангенс острого угла между пересекающимися прямыми можно найти, используя формулу:
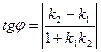, (11)
откуда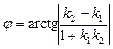 
. Если одна из прямых вертикальная, т.е. k 2 не существует, то 
.
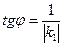Справочный материал по теме «Аналитическая геометрия В ПРОСТРАНСТВЕ» (задачА 2)
Уравнение плоскости в пространстве
Общее уравнение плоскости: 
,
где A, B, C – координаты вектора нормали вектора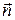 
(любого вектора, перпендикулярного данной плоскости), D – свободный член уравнения.
Уравнение плоскости, проходящей через точку 
перпендикулярно вектору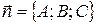 
:
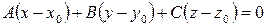. (12)
Уравнение плоскости, проходящей через три заданные точки 
:
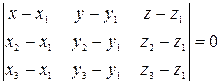. (13)
Угол 
между двумя плоскостями, заданными уравнениями 
и 
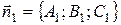определяется как угол между векторами их нормалей 
и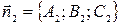 
или дополнительный к нему (обычно берется острый угол), то есть
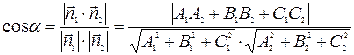. (14)
