Общие и специальные методы повышения надежности.

 

Наиболее жесткие требования по надежности предъявляются к космической РЭА и РЭА специального назначения. При этом необходимо еще учитывать, что указанные категории аппаратуры подвергаются сложным климатическим и механическим воздействиям Для таких категорий аппаратуры высокие требования по надежности не могут быть обеспечены только за счет общих мер надежности. К общим мерам по обеспечению заданной высокой надежности относятся:

– четкая регламентация условий эксплуатации изделия;

– оптимальный выбор функциональной схемы изделия;

– выбор для изделия комплектующих элементов, обладающих высокой надежностью и стабильностью характеристик, проведение схемных и конструкторских мероприятий, обеспечивающих щадящие режимы работы элементов в устройстве;

– реализация технологических мероприятий, обеспечивающих бездефектное изготовление устройств;

– проведение всесторонних конструкторских отбраковочных испытаний макетов и опытных образцов устройств, обеспечивающих наиболее полное выявление и устранение слабых мест схемы и конструкции еще на этапе разработки;

– создание системы всесторонних производственных испытаний, обеспечивающих выявление производственных дефектов аппаратуры и ее элементов;

– создание системы наблюдения за качеством работы устройств в эксплуатации, проведение профилактических мер и т.д.

Специальные методы повышения надежности связаны с введением в схему дополнительных элементов, предназначенных для повышения надежности устройства.

В теории надежности, прежде чем провести анализ радиотехнического устройства на надежность, принято переходить от электрической принципиальной схемы к эквивалентной структурной схеме надежности. В основу такого перехода положены принятые в теории надежности понятия последовательного, параллельного и смешанного вида соединения элементов, которые не следует путать с аналогичными видами электрических соединений. Виды соединения в теории надежности показаны на рис. 3.4.

 

Рис.3.4. Виды соединений в теории надежности

а – основное; б – резервное; в – смешанное.

Последовательным, или основным, называется такое соединение элементов системы, при котором отказ хотя бы одного из элементов приводит к отказу системы в целом (рис.3.4,а).

Параллельным, или резервным, соединением элементов системы называют такое соединение, при котором отказ системы наступает лишь в случае отказа всех ее элементов (рис. 3.4,б).

Смешанным соединением элементов называют сочетание основного и резервного видов соединений или более сложные структуры (рис.3.4,в).

Наиболее эффективными мерами повышения надежности на этапе проектирования является применение резервирования.

Резервирование – это метод повышения надежности путем введения запасных (резервных) элементов, являющихся избыточными по отношению к функциональной структуре РЭА, необходимой для выполнения заданных функций. Аппаратура с избыточными элементами называется резервированной. В резервированном изделии отказ наступает тогда, когда выйдут из строя все резервные устройства. Применяемые в теории надежности способы резервирования показана на рис.3.5.

 

	Резервирование

 

 

 

Резерв ненагруженный

 

Рис.3.5. Способы резервирования.

 

Основным параметром резервирования является кратность резервирования. Под кратностью резервирования понимают отношение числа резервных изделий к числу основных (резервируемых). Кратность резервирования обозначается m. Различают резервирование с целой и дробной кратностью. Например, если m =3, то это означает, что число резервных устройств равно трем, основное устройство одно, а общее число устройств равно четырем. Это резервирование с целой кратностью. Если m = 4/2, то это резервирование с дробной кратностью, при котором число резервных устройств равно четырем, число основных – двум, а число устройств – шести (сократить дробь нельзя, т.к. если m = 4/2 = 2, то это резервирование с целой кратностью, при котором число резервных устройств два, основное одно, а общее число устройств три).

В зависимости от масштаба и принятой единицы резервирования различают общий и раздельный способы резервирования. При общем резервировании резервируется вся система в целом. Общее резервирование в зависимости от способа включения резервных устройств можно разделить на постоянное резервирование и резервирование замещением.

При общем постоянном резервировании резервные устройства подключены к основным в течение всего времени работы и находятся в одинаковом с ними режиме. Схема общего постоянного резервирования показана на рис.3.6.

 

 

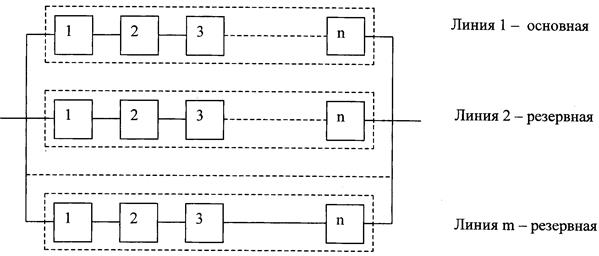
Рис.3.6. Структурная схема общего постоянного резервирования.

 

При общем постоянном резервировании может использоваться только нагруженный резерв, что требует полного состава запасных элементов, ведет к увеличению габаритов и массы системы и повышенному расходу энергии. Кроме того, резервные элементы в этом случае «стареют» в так же степени, как и основные рабочие элементы. Указанные факторы несомненно относятся к недостаткам данного вида резервирования. Основные характеристики надежности при общем постоянном резервировании с целой кратностью можно рассчитать по формулам:

P(t)_p = 1 – [1 – P(t)] ^m+1 (3.15)

 

где P(t)_p – вероятность безотказной работы резервированной системы;

P(t) = е^-λtp – вероятность безотказной работы нерезервированной системы при экспоненциальном законе распределения надежности;

m – кратность резервирования.

_m

Т_{ср. р} = Т_ср · Σ 1 / (i + 1) = Т_ср [(1+ 1/2 + … + 1/ (m + 1)] (3.16)

ⁱ⁼⁰

где Т_{ср. р} – средняя наработка на отказ резервированной системы;

Т_ср. – средняя наработка на отказ нерезервированной системы.

Для наиболее простого случая, когда m = 1, получим:

 

P(t)_p = 1 – [1 – P(t)] ² (3.17)

 

Т_{ср. р} = 1,5 Т_ср (3.18)

 

Таким образом, при одном основном и одном резервном устройстве средняя наработка на отказ увеличивается в 1,5 раза. К преимуществам общего постоянного резервирования относятся:

– относительная простота построения схем;

– отсутствие хотя бы кратковременного перерыва в работе при отказе одного или даже нескольких элементов системы;

– отсутствие дополнительных подключающих элементов, снижающих общую надежность системы.

 

При резервировании замещением резервные изделия замещают основные только после их отказа. Схема общего резервирования замещением показана на рис.3.7.

 

 

Рис.3.7. Структурная схема общего резервирования

замещением с целой кратностью.

 

При включении резерва по способу замещения резервные элементы до момента их включения в работу могут находиться в различных состояниях. Исходя из возможных режимов работы резервных элементов, различают резервы:

– нагруженный;

– облегченный;

– ненагруженный.

При резервировании замещением резервное устройство включается в работающую систему с помощью автоматических устройств или вручную. При автоматическом включении требуется чрезвычайно высокая надежность переключающих элементов. При большом количестве и невысокой надежности этих дополнительных элементов, входящих в резервированную систему, ее надежность может понизиться по сравнению с надежностью нерезервированной системы. Кроме того, даже при высокой степени быстродействия переключающих элементов имеется перерыв в работе системы на время переключения на резервные устройства. Следует заметить, что при ручной замене отказавших элементов возрастает время переключения, но надежность оператора, выполняющего функции переключающего устройства, может быть принята за единицу.

 

При использовании нагруженного резерва запасные резервные элементы находятся в том же режиме работы, что и основной элемент, независимо от того, участвуют они в работе схемы или нет. Если при этом основной и резервный элементы идентичны, то интенсивности их отказов совпадают и надежность основного и резервного устройств одинакова. При использовании нагруженного резерва, если не учитывать надежность автоматических переключающих устройств, характеристики надежности можно рассчитывать по тем же формулам, что и для общего постоянного резервирования.

 

При использовании ненагруженного резерва запасные резервные элементы до момента их включения в работающую схему полностью обесточены. В этом случае резервные устройства имеют самую высокую надежность по сравнению с основными элементами, поэтому общее резервирование замещением с использованием ненагруженного резерва обеспечивает наилучшие показатели для общего резервирования. Характеристики надежности в этом случае рассчитывают по формулам:

_m

P(t)_p = P(t) ∙ ∑ (t_p / T_ср)ⁱ∙ 1 / i! = P(t) ∙ [(1 + t_p/T_ср + 1/2! (t_p/T_ср)² + … + 1/m!(t_p/T_ср)^m] (3.19)

ⁱ⁼⁰

Т_{ср. р} = Т_ср (m + 1) (3.20)

 

где P(t)_p и P(t) – вероятность безотказной работы резервированной и нерезервированной систем;

Т_{ср. р} и Т_ср – средняя наработка на отказ резервированной и нерезервированной систем;

m – кратность резерирования.

Для наиболее простого случая, когда m = 1, получим:

 

P(t)_p = P(t) ∙ (1 + t_p / T_ср ) (3.21)

Т_{ср. р} = 2 Т_ср (3.22)

Таким образом, при использовании ненагруженного резерва средняя наработка на отказ увеличивается как минимум в два раза.

При использовании облегченного резерва резервные элементы до момента их включения в работающую схему находятся в облегченном электрическом режиме. Например, для полупроводниковых схем облегченный режим обеспечивается за счет пониженного напряжения на коллекторах транзисторов по сравнению номинальным рабочим режимом. Надежность каждого резервного элемента в этом случае выше надежности соответствующего основного элемента.

Показатели надежности в случае использования облегченного резерва занимают среднее положение, т.е.

Т_{ср р ненагр} > Т_{ср р обл} > Т _{ср р нагр}

 

Использование облегченного или ненагруженного резерва дает возможность снизить расход электроэнергии и увеличить надежность аппаратуры, т.к. надежность резервных устройств в этом случае всегда выше, чем основных. Следовательно, резервирование замещением позволяет улучшить показатели надежности и продлить срок службы РЭА. Однако не следует забывать о недостатках, основным из которых является наличие переключающих устройств., имеющих свои показатели надежности и обладающих определенной инерционностью, что приводит к появлению конечного времени переключения с основного блока на резервные, а в некоторых видах РЭА это недопустимо. Поэтому резервирование замещением применяется для систем, допускающих перерывы в работе. Кроме того, при нагруженном и облегченном резервах увеличиваются потребляемые мощности.

При раздельном резервировании резервируются отдельные составные части изделия, т.е. вводится индивидуальный резерв для каждого элемента, узла, блока неизбыточной системы. Раздельное резервирование бывает постоянным и замещаемым, Схемы раздельного резервирования показаны на рис.3.8. Раздельное резервирование может быть поэлементным, покаскадным, узловым, блочным и т.д. и используется в сложных системах, в которых требуемые показатели надежности не удается получить рассмотренными выше способами резервирования. При раздельном резервировании отказ системы может произойти только тогда, когда отказ произойдет дважды подряд в одном и том же устройстве (m = 1), что маловероятно. Поэтому показатели надежности при раздельном резервировании значительно выше. Для оценки надежности при раздельном резервировании используется специфический и сложный математический аппарат. Математический анализ таких систем показывает, что наиболее высокие показатели надежности можно получить, используя раздельное резервирование замещением с ненагруженным резервом.

Рис.3.8. Структурная схема раздельного резервирования.

а – раздельное постоянное с целой кратностью; б – раздельное

замещением с целой кратностью.

 

 

Эффективность резервирования принято оценивать с помощью коэффициента повышения надежности γ. Коэффициент повышения надежности определяется по показателям безотказности из соотношений:

 

γ _p = P(t)_p / P(t)

γ _Q = Q(t) / Q(t)_p

 

где P(t)_p, Q(t)_p и Q(t), P(t) – вероятность безотказной работы и вероятность отказа для резервированной и нерезервированной систем. Следует заметить, что независимо от способа резервирования РЭА введение резерва всегда влечет за собой резкое возрастание габаритов, массы и стоимости аппаратуры, а в отдельных случаях и потребление мощности, поэтому использовать резервирование необходимо в технически и экономически обоснованных случаях. Целесообразность применения резервирования определяется следующими факторами:

– исходным уровнем надежности комплектующих изделий;

– заданным временем эксплуатации;

– наличием эффективной системы контроля и периодичностью профилактики;

– возможностью использования других, менее избыточных методов повышения надежности.

Анализ резервированных систем показывает, что интенсивность отказов резервированной системы быстро возрастает с течением времени, хотя интенсивность отказов нерезервированной системы от времени не зависит, что показано на рис.3.9 для общего и раздельного резервирования.

 

Рис. 3.9. Зависимость интенсивности отказов

резервированной системы от времени.

1 – общее резервирование; 2 – раздельное резервирование.

 

Из графика следует, что для резервированных систем существует такой момент времени t_kp, после которого использование резервированной системы не оправдано. Поэтому если не учитывать особенности профилактики систем, то резервирование более выгодно применять для систем кратковременного действия, когда t << t_kp, тогда как для систем длительного использования, когда t >> t_kp, целесообразно использовать другие методы повышения надежности. Выбор метода повышения надежности и выбор конкретного способа резервирования в значительной степени определяются категорией РЭА. Например, для современных сложных вычислительных комплексов, насчитывающих сотни и тысячи узлов и блоков, использование резервирования замещением может привести к простою машины, необходимости повторения программ, что снижает оперативность решения задачи. Поэтому вытекает необходимость использования постоянного резервирования или разумного сочетания постоянного резервирования с резервированием замещением. Методы резервирования эффективные для цифровых устройств, могут оказаться малопригодными для устройств аналогового типа. Для аналоговых устройств чаще может использоваться резервирование замещением, что объясняется отсутствием взаимного влияния основного и резервного каналов. Таким образом, разнообразие существующих категорий РЭА затрудняет построение общих конструктивных подходов и единых требований по надежности. Поэтому выбор показателей, принятие решения о введении различных методов, повышающих надежность, делают дифференцировано в зависимости от категории проектируемой аппаратуры.

 

 

4. КОМПОНОВКА ЭЛЕКТРОННОЙ АППАРАТУРЫ.