 При движении твердого тела с двумя неподвижными точками
При движении твердого тела с двумя неподвижными точками 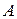 и
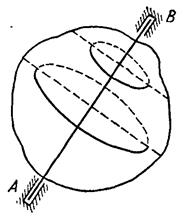
и 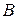 (рис. 10.4) все точки на прямой
(рис. 10.4) все точки на прямой 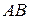 остаются неподвижными. Это следует из условия неизменяемости расстояний между точками твердого тела. Прямая
остаются неподвижными. Это следует из условия неизменяемости расстояний между точками твердого тела. Прямая 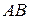 называется осью вращения, а движение тела называется вращательным. Нетрудно видеть, что все точки тела описывают дуги окружностей с центрами в основаниях перпендикуляров, опущенных из этих точек на ось вращения.
называется осью вращения, а движение тела называется вращательным. Нетрудно видеть, что все точки тела описывают дуги окружностей с центрами в основаниях перпендикуляров, опущенных из этих точек на ось вращения.

 Возьмем на оси вращения две точки
Возьмем на оси вращения две точки 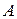 и
и 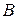 и введем систему координат
и введем систему координат 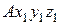 с началом в точке
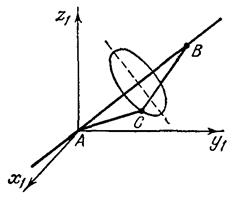
с началом в точке 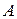 (рис. 10.5). Так как положение точек
(рис. 10.5). Так как положение точек 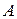 и
и 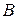 нам известно, то положение тела будет полностью определено, если мы будем знать в любой момент времени положение какой-либо точки
нам известно, то положение тела будет полностью определено, если мы будем знать в любой момент времени положение какой-либо точки 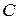 тела (не лежащей на оси вращения). Из трех координат этой точки независимой будет только одна, так как расстояния
тела (не лежащей на оси вращения). Из трех координат этой точки независимой будет только одна, так как расстояния 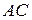 и
и 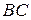 постоянны и координаты точки связаны двумя уравнениями:
постоянны и координаты точки связаны двумя уравнениями:
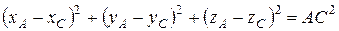 ,
,
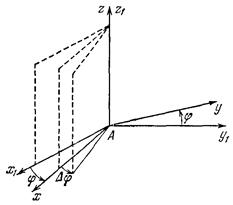
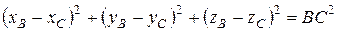 .
.
Отсюда следует, что положение твердого тела, вращающегося вокруг неподвижной оси, определяется одним параметром.
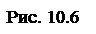 Направим ось
Направим ось 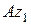 неподвижной системы координат
неподвижной системы координат 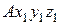 по оси вращения тела. Введем подвижную систему координат
по оси вращения тела. Введем подвижную систему координат 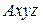 , жестко связанную с телом, ось
, жестко связанную с телом, ось 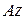 которой так же направим по оси вращения (рис. 10.6). Положение тела будет полностью определено, если задан угол
которой так же направим по оси вращения (рис. 10.6). Положение тела будет полностью определено, если задан угол 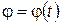 между неподвижной плоскостью
между неподвижной плоскостью 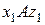 и подвижной плоскостью (жестко связанной с телом)
и подвижной плоскостью (жестко связанной с телом) 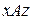 (рис. 10.6). Этот угол называется углом поворота тела.
(рис. 10.6). Этот угол называется углом поворота тела.
Для однозначного определения положения тела необходимо знать не только величину, но и направление отсчета угла 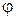 . Условимся считать положительным направлением отсчета направление против хода часовой стрелки, если смотреть с конца оси
. Условимся считать положительным направлением отсчета направление против хода часовой стрелки, если смотреть с конца оси 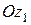 .
.
Характер вращательного движения твердого тела целиком определяется заданием угла его поворота как функции времени. Главными кинематическими характеристиками вращательного движения тела в целом будут угловая скорость и угловое ускорение. Рассмотрим эти понятия.
Пусть в момент времени 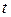 угол между неподвижной полуплоскостью
угол между неподвижной полуплоскостью 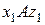 и подвижной полуплоскостью
и подвижной полуплоскостью 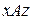 равен
равен 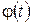 , а в момент времени
, а в момент времени 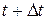 равен
равен 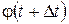 . Это значит, что за промежуток времени
. Это значит, что за промежуток времени 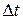 подвижная плоскость, а следовательно, и тело повернулись на угол
подвижная плоскость, а следовательно, и тело повернулись на угол 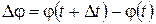 .
.
Отношение угла поворота 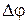 к промежутку времени
к промежутку времени 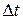 , за который тело повернулось на этот угол, называется средней угловой скоростью тела за промежуток времени
, за который тело повернулось на этот угол, называется средней угловой скоростью тела за промежуток времени 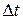 :
: 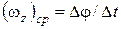 . Предел этого отношения при
. Предел этого отношения при 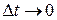 называется угловой скоростью тела в данный момент времени
называется угловой скоростью тела в данный момент времени
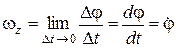 . (10.5)
. (10.5)
Абсолютное значение угловой скорости будем обозначать через 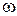 , т. е.
, т. е. 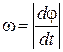 . Если угол поворота измеряется в радианах, а время – в секундах, то единицей измерения угловой скорости будет
. Если угол поворота измеряется в радианах, а время – в секундах, то единицей измерения угловой скорости будет 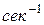 . В технике часто при равномерном вращении тела пользуются числом оборотов в минуту. Зависимость между угловой скоростью и числом оборотов в минуту определяется по следующей формуле:
. В технике часто при равномерном вращении тела пользуются числом оборотов в минуту. Зависимость между угловой скоростью и числом оборотов в минуту определяется по следующей формуле: 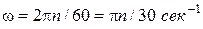 , где
, где 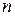 – число оборотов в минуту.
– число оборотов в минуту.
Пусть теперь в момент времени 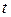 угловая скорость вращения равна
угловая скорость вращения равна  , а в момент
, а в момент 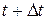 равна
равна 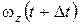 ; тогда за промежуток времени
; тогда за промежуток времени 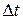 приращение угловой скорости будет равно
приращение угловой скорости будет равно 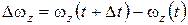 .
.
Средним угловым ускорением тела за промежуток времени 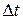 будем называть отношение приращения угловой скорости к промежутку времени, за который это изменение произошло, т. е.
будем называть отношение приращения угловой скорости к промежутку времени, за который это изменение произошло, т. е. 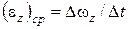 .
.
Предел этого отношения при 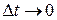 называется угловым ускорением тела в данный момент времени
называется угловым ускорением тела в данный момент времени
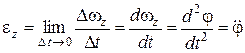 . (10.6)
. (10.6)
Угловое ускорение, характеризующее изменение угловой скорости с течением времени, равно производной по времени от угловой скорости или второй производной по времени от угла поворота. Единица измерения углового ускорения – 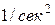 .
.
Введём в рассмотрение понятия вектора угловой скорости и вектора углового ускорения.
Вектором угловой скорости твердого тела, совершающего вращение вокруг неподвижной оси, мы будем называть вектор, модуль которого равен абсолютному значению производной угла поворота тела по времени, направленный вдоль оси вращения в ту сторону, откуда вращение тела видно происходящим против хода часовой стрелки.
Учитывая ранее введенное определение направления положительного отсчета угла 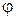 , вектор угловой скорости можно определить по формуле
, вектор угловой скорости можно определить по формуле
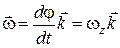 , (10.7)
, (10.7)
где 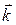 – единичный вектор оси
– единичный вектор оси 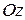 .
.
Вектором углового ускорения будем называть вектор, равный производной по времени от вектора угловой скорости, т: е.
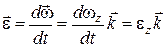 . (10.8)
. (10.8)
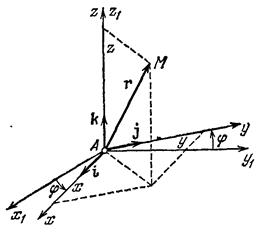 Из формулы (10.8) следует, что вектор
Из формулы (10.8) следует, что вектор 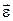 направлен, как и вектор
направлен, как и вектор 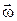 , вдоль оси вращения. Величины
, вдоль оси вращения. Величины  и
и 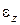 представляют проекции векторов угловой скорости
представляют проекции векторов угловой скорости 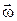 и углового ускорения
и углового ускорения 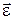 на ось вращения.
на ось вращения.
Перейдем к нахождению скорости и ускорения любой точки тела, вращающегося вокруг неподвижной оси. Пусть единичные векторы координатных осей 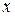 ,
, 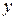 ,
, 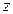 , соответственно будут
, соответственно будут 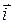 ,
, 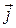 и
и 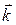 (рис. 10.7). Радиус-вектор произвольной точки
(рис. 10.7). Радиус-вектор произвольной точки 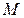 можно представить в виде
можно представить в виде

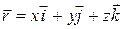 , (10.9)
, (10.9)
где 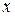 ,
, 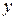 ,
, 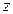 – координаты точки (постоянные величины).
– координаты точки (постоянные величины).
Скорость точки 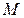 будет равна
будет равна
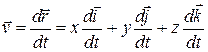 . (10.10)
. (10.10)
Так как вектор 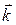 неподвижен, то
неподвижен, то 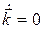 . Производные векторов
. Производные векторов 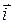 и
и 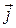 уже вычислялись при рассмотрении движение точки в полярной системе координат. Если обозначить
уже вычислялись при рассмотрении движение точки в полярной системе координат. Если обозначить 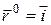 и
и 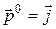 , то формулы (9.15) и (9.16) (предыдущей лекции) примут вид
, то формулы (9.15) и (9.16) (предыдущей лекции) примут вид
 ,
, 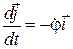 .
.
Подставляя в формулу (10.10) эти производные и учитывая, что 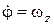 , получим
, получим 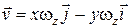 . Отсюда следует, что проекции вектора скорости точки
. Отсюда следует, что проекции вектора скорости точки 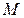 на оси
на оси 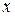 ,
, 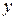 и
и 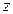 соответственно равны
соответственно равны 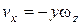 ,
, 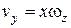 ,
, 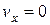 .
.
Так как векторное произведение 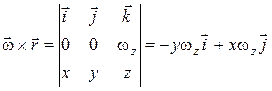 имеет те же проекции на оси
имеет те же проекции на оси 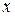 ,
, 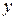 и
и 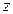 , что и вектор скорости
, что и вектор скорости 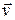 , то имеем
, то имеем
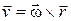 . (10.13)
. (10.13)
Таким образом, скорость любой точки твердого тела, вращающегося вокруг неподвижной оси, равна векторному произведению вектора угловой скорости тела на радиус-вектор этой точки.
Из формулы (10.13) следует, что 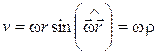 , т. е. модуль скорости любой точки твердого тела равен произведению модуля угловой скорости тела на расстояние от точки до оси вращения. Направлен же вектор скорости по касательной к окружности, по которой перемещается точка
, т. е. модуль скорости любой точки твердого тела равен произведению модуля угловой скорости тела на расстояние от точки до оси вращения. Направлен же вектор скорости по касательной к окружности, по которой перемещается точка 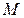 , в сторону ее движения.
, в сторону ее движения.
Взяв производную по времени от обеих частей равенства (10.13), получим
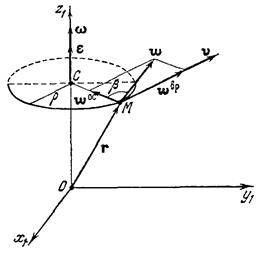
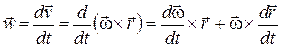 .
.
Но 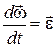 – угловое ускорение, а
– угловое ускорение, а
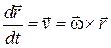 – скорость точки
– скорость точки 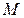 . Тогда
. Тогда
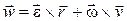 .
.
 Вектор
Вектор 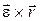 направлен по касательной к траектории точки (к окружности радиуса
направлен по касательной к траектории точки (к окружности радиуса 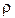 ), т. е. параллельно скорости (так как вектор
), т. е. параллельно скорости (так как вектор 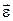 направлен по оси вращения (рис. 10.8)). Эта составляющая ускорения является касательным ускорением точки
направлен по оси вращения (рис. 10.8)). Эта составляющая ускорения является касательным ускорением точки 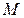 тела. В дальнейшем будем называть эту составляющую вращательным ускорением, т. е.
тела. В дальнейшем будем называть эту составляющую вращательным ускорением, т. е.
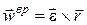 .
.
Численное значение вращательного ускорения равно 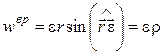 .
.
Вектор 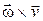 направлен в плоскости окружности радиуса
направлен в плоскости окружности радиуса 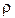 от точки
от точки 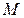 к точке
к точке 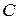 , т. е. направлен к оси вращения по нормали к траектории и является нормальным ускорением точки
, т. е. направлен к оси вращения по нормали к траектории и является нормальным ускорением точки 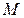 . Этот вектор
. Этот вектор 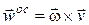 , направленный к оси вращения, будем называть осестремительным ускорением.
, направленный к оси вращения, будем называть осестремительным ускорением.
Так как вектор 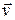 перпендикулярен вектору
перпендикулярен вектору 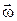 , то численное значение осестремительного ускорения равно
, то численное значение осестремительного ускорения равно
 .
.
Модуль полного ускорения точки 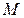 будет
будет
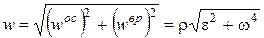 .
.
Угол 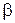 , образованный векторами полного и осестремительного ускорений, определяется из формулы
, образованный векторами полного и осестремительного ускорений, определяется из формулы
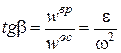 .
.






