Шифрование одиночной перестановкой по ключу.

Содержание

Введение

1. Порядок выполнения курсовой работы.....................................................3

2. Варианты заданий........................................................................................3

3. Методические указания...............................................................................5

4. Структура и содержание пояснительной записки.................................5

5. Литература....................................................................................................5

Приложение 1..............................................................................................7

Приложение 2 Структура и содержание пояснительной записки........15

Приложение 3. Титульний лист.............................................................17

Введение

Курсовая работа предназначена для формирования у студентов навыков самостоятельной научно-исследовательской деятельности, практической деятельности, грамотного оформления полученных результатов в печатном виде, представления результатов своей работы в виде пояснительной записки в рамках дисциплины «Программное обеспечение систем защиты информации».

Целью курсовой работы является закрепление и углубление знаний, полученных студентами в курсе «Программное обеспечение систем защиты информации» и разработка программного средства защиты информации.

Порядок выполнения курсовой работы

Курсовая работа по курсу «Программное обеспечение систем защиты информации» выполняется индивидуально каждым студентом в соответствии с выданным преподавателем вариантом. Курсовая работа выполняется в среде Delphi на языке Object Pascal.

В процессе работы студент должен:

1. Освоить метод программной защиты информации.

2. Выбрать форму представления исходных данных и результатов.

3. Разработать алгоритмы, используемые при решении задачи.

4. Разработать пользовательский интерфейс для ввода и получения информации.

5. Провести отладку и тестирование программы.

6. Оформить документацию программы.

Все этапы работы должны быть отражены в пояснительной записке.

Варианты заданий

1. Шифрування методом простої підстановки.

2. Шифрування методом афінною системою підстановки Цезаря.

3. Шифрування методом підстановки Цезаря з ключовим словом.

4. Шифрування методом таблиць Трисемуса.

5. Шифрування методом біграм Плейфейра.

6. Шифрування методом багатоалфавітної одноконтурної звичайної підстановки.

7. Шифрування методом багатоалфавітної одноконтурної монофонічної підстановки.

8. Шифрування методом багатоалфавітної багатоконтурної підстановки.

9. Шифрування методом «подвійний квадрат» Уітстона.

10. Шифрування методом простого переміщення.

11. Шифрування методом одиничного переміщення за ключем.

12. Шифрування методом подвійного переміщення.

13. Шифрування методом магічних квадратів.

14. Шифрування методом ускладненого переміщення за таблицею.

15. Шифрування методом ускладненого переміщення за маршрутами.

16. Шифрування методом з кінцевою короткою гамою (символи алфавіту представляються у цифровому еквіваленті, а довжина гами дорівнює 5 елементів).

17. Шифрування методом з кінцевою короткою гамою (символи алфавіту представляються у вигляді двійкового коду, а довжина гами дорівнює 5 елементів).

18. Шифрування методом з кінцевою короткою гамою (символи алфавіту представляються у цифровому еквіваленті, а довжина гами дорівнює 7 елементів).

19. Шифрування методом з кінцевою короткою гамою (символи алфавіту представляються у вигляді двійкового коду, а довжина гами дорівнює 7 елементів).

20. Шифрування методом з кінцевою довгою гамою (символи алфавіту представляються у цифровому еквіваленті 10 елементів).

21. Шифрування методом з кінцевою довгою гамою (символи алфавіту представляються у вигляді двійкового коду 10 елементів).

22. Шифрування методом з кінцевою довгою гамою (символи алфавіту представляються у цифровому еквіваленті 20 елементів).

23. Шифрування методом з кінцевою довгою гамою (символи алфавіту представляються у вигляді двійкового коду 20 елементів).

24. Шифрування методом з кінцевою довгою гамою (символи алфавіту представляються у цифровому еквіваленті 27 елементів).

25. Шифрування методом з кінцевою довгою гамою (символи алфавіту представляються у вигляді двійкового коду 27 елементів).

26. Шифрування методом з кінцевою довгою гамою (символи алфавіту представляються у цифровому еквіваленті 40 елементів).

27. Шифрування методом з кінцевою довгою гамою (символи алфавіту представляються у вигляді двійкового коду 40 елементів).

28. Шифрування методом з безкінечною гамою (символи алфавіту представляються у цифровому еквіваленті).

29. Шифрування методом з безкінечною гамою (символи алфавіту представляються у вигляді двійкового коду).

30. Шифрування методом з використанням аналітичних перетворень за правилами алгебри матриць.

Примерный вид формы приложения по некоторым вариантам

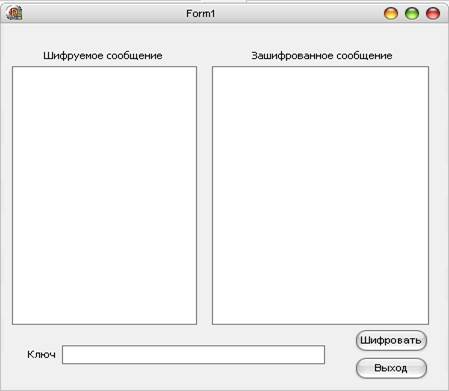
Методические указания

Курсовая работа выполняется в среде Delphi как Windows -приложение.

При выполнении курсовой работы обязательным является использование методов и средств объектно-ориентированного программирования.

Методы шифрования данных рассмотрены в Приложении 1.

Структура и содержание пояснительной записки

Структура, содержание и рекомендации по оформлению пояснительной записки приведены в Приложениях 2, 3.

К пояснительной записке прилагается диск с файлами разработанного проекта.

Литература

1. Вирт Н. Алгоритмы + структуры данных = программы. – М.: Мир, 1985.

2. Буч Г. Объектно-ориентированное проектирование с примерами применения. 1992.

3. Дантеманн Д., Мишел Д., Тейлор Д. Программирование в среде Delphi. – К.: НИПФ «ДиаСофт Лтд.», 1995.

4. Немнюгин С.А. Turbo Pascal. – СПб.: Изд-во «Питер», 2000.

5. Гофман В.Э., Хомоненко А.Д. Работа с базами данных в Delphi. – СПб.: БХВ – Санкт-Петербург, 2003.

6. Гофман В.Э., Хомоненко А.Д. Delphi 6. – СПб.: БХВ – Санкт-Петербург, 2001.

7. Фаронов В.В. Delphi 6: Учебный курс. – М.:, 2001.

8. Культин Н.Б. Delphi 6. Программирование на Object Pascal.

9. Ставровский А.Б. Первые шаги в программировании. Самоучитель. – М.: Издательский дом «Вильямс», 2003.

10. Галисеев Г.В. Программирование в среде Delphi 7. Самоучитель. – М.: Издательский дом «Вильямс», 2004.

11. 32 урока по Delphi. http://books.kulichki.net/data/delphi/del2/.

12. Флёнов М.Е. Библия Delphi. СПб.: БХВ-Петербург, 2005.

Приложение 1

Шрифты перестановки

Шифрование простой перестановкой.

Для простой перестановки ключом служит размер таблицы.

Например:

ТЕРМИНАТОР ПРИБЫВАЕТ СЕДЬМОГО В ПОЛНОЧЬ

записывается в таблицу поочередно по столбцам.

 

Т	Н	П	В	Е	Г	Л
Е	А	Р	А	Д	О	Н
Р	Т	И	Е	Ь	В	О
М	О	Б	Т	М	П	Ч
И	Р	Ы	С	О	О	Ь

 

После заполнения таблицы текстом сообщения по столбцам для формирования шифртекста считывают содержимое таблицы по строкам. Если шифртекст записывать группами по пять букв, получается такое шифрованное сообщение:

 

ТНПВЕ ГЛЕАР АДОНР ТИЕЬВ ОМОБТ МПЧИР ЫСООЬ

 

Естественно, отправитель и получатель сообщения должны заранее условиться об общем ключе в виде размера таблицы. Следует заметить, что объединение букв шифртекста в 5-буквенные группы не входит в ключ шифра и осуществляется для удобства записи несмыслового текста. При расшифровании действия происходят в обратном порядке.

Шифрование одиночной перестановкой по ключу.

Этот метод отличается от предыдущего тем, что столбцы таблицы переставляются по ключевому слову, фразе или набору чисел длиной в строку таблицы.

Применим в качестве ключа, например, слово

ПЕЛИКАН,

а текст сообщения возьмем из предыдущего примера.

 

Ключ П	Е	Л	И	К	А	Н
Т	Н	П	В	Е	Г	Л
Е	А	Р	А	Д	О	Н
Р	Т	И	Е	Ь	В	О
М	О	Б	Т	М	П	Ч
И	Р	Ы	С	О	О	Ь

До перестановки

 

А	Е	И	К	Л	Н	П
Г	Н	В	Е	П	Л	Т
О	А	А	Д	Р	Н	Е
В	Т	Е	Ь	И	О	Р
П	О	Т	М	Б	Ч	М
О	Р	С	О	Ы	Ь	И

После перестановки

В верхней строке левой таблицы записан ключ, а номера под буквами ключа определены в соответствии с естественным порядком соответствующих букв ключа в алфавите. Если бы в ключе встретились одинаковые буквы, они бы были понумерованы слева направо. В правой таблице столбцы переставлены в соответствии с упорядоченными номерами букв ключа.

При считывании содержимого правой таблицы по строкам и записи шифртекста группами по пять букв получим шифрованное сообщение:

 

ГНВЕП ЛТООА ДРНЕВ ТЕЬИО РПОТМ БЧМОР СОЫЬИ

 

Шифрование двойной перестановкой.

В случае двойной перестановки столбцов и строк таблицы перестановки определяются отдельно для столбцов и отдельно для строк. Сначала в таблицу записывается текст сообщения, а потом поочередно переставляются столбцы, а затем строки. При расшифровании порядок перестановок должен быть обратным.

Например:

ПРИЛЕТАЮ ВОСЬМОГО

 

	П	Р	И	Л
	Е	Т	А	Ю
	В	О	С	Ь
	М	О	Г	О

Исходная таблица

 

	Р	Л	И	П
	Т	Ю	А	Е
	О	Ь	С	В
	О	О	Г	М

Перестановка столбцов

 

	Т	Ю	А	Е
	О	О	Г	М
	Р	Л	И	П
	О	Ь	С	В

Перестановка строк

Если считывать шифртекст из правой таблицы построчно блоками по четыре буквы, то получится следующее:

ТЮАЕ ООГМ РЛИП ОЬСВ

Ключом к шифру двойной перестановки служит последовательность номеров столбцов и номеров строк исходной таблицы (в нашем примере последовательности 4132 и 3142 соответственно).

Шифрование методом магических квадратов.

Магическими квадратами называют квадратные таблицы с вписанными в их клетки последовательными натуральными числами, начиная от 1, которые дают в сумме по каждому столбцу, каждой строке и каждой диагонали одно и тоже число.

Шифруемый текст записывается в магические квадраты в соответствии с нумерацией их клеток. Если затем выписать содержимое такой таблицы по строкам, то получится шифртекст, сформированный благодаря перестановке букв исходного сообщения.

Например:

ПРИЛЕТАЮ ВОСЬМОГО

 

О	И	Р	М
Е	О	С	Ю
В	Т	А	Ь
Л	Г	О	П

Шифртекст, получаемый при считывании содержимого правой таблицы по строкам:

 

ОИРМ ЕОСЮ ВТАЬ ЛГОП

Усложненный метод перестановки по таблицам.

Усложненный метод перестановки по таблицам заключается в том, что для записи символов шифруемого текста используется специальная таблица, в которую введены некоторые усложняющие элементы. Таблица представляет собой матрицу, размеры которой могут быть выбраны произвольно (например 10 ´ 10). В нее, как и в случае простой перестановки, записываются знаки шифруемого текста. Усложнение состоит в том, что определенное число клеток таблицы не используется. Количество и расположение неиспользуемых элементов является дополнительным ключом шифрования. Шифруемый текст блоками по m ´ n – S элементов записывается в таблицу (m ´ n — размеры таблицы, S — количество неиспользуемых элементов). Далее процедура шифрования аналогична простой перестановке.

Варьируя размерами таблицы, последовательностью символов ключа, количеством и расположением неиспользуемых элементов, можно получить требуемую стойкость зашифрованного текста.

Усложненный метод перестановок по маршрутам.

Весьма высокую стойкость шифрованию можно обеспечить, используя усложненный метод перестановок по маршрутам типа гамильтоновских. При этом для записи символов шифруемого текста используются вершины некоторого гиперкуба, а знаки зашифрованного текста считываются по маршрутам Гамильтона, причем используется несколько различных маршрутов (рис. 1).

Следует заметить, что все процедуры шифрования и расшифровки по методу перестановки являются в достаточной степени формализованным и могут быть реализованы алгоритмически.

 

 

Рис. 1. Схема шифрования перестановкой по маршрутам Гамильтона. Открытый текст "КРИПТОГР", зашифрованный текст — "ТОРКИПРГ" (вверху) и "ТКИПРОРГ" (внизу)

Шифрование заменой.

При шифровании заменой (подстановкой) символы шифруемого текста заменяются символами того же или другого алфавита с заранее установленным правилом замены.

Шифрование простой заменой.

В шифре простой замены каждый символ исходного текста заменяется символами того же алфавита одинаково на всем протяжении текста. Часто шифры простой замены называют шифрами одноалфавитной подстановки.

Частным случаем шифра простой замены является шифр Цезаря.

При шифровании исходного текста каждая буква заменялась на другую букву того же алфавита по следующему правилу. Заменяющая буква определялась путем смещения по алфавиту от исходной буквы на К букв. При достижении конца алфавита выполнялся циклический переход к его началу. Цезарь использовал шифр замены при смещении К=3.

Например:

 

VENI VIDI VICI (В ПЕРЕВОДЕ НА РУССКИЙ «Пришел, Увидел, Победил»

в зашифрованном виде: YHQL YLGL YLFL

 

Таблица соответствия для шифрования методом Цезаря

 

A®D	J®M	S®V
B®E	K®N	T®W
C®F	L®O	U®X
D®G	M®P	V®Y
E®H	N®Q	W®Z
F®I	O®R	X®A
G®J	P®S	Y®B
H®K	Q®T	Z®C
I®L	R®U

Шифрование аффинной системой подстановок Цезаря.

Этот шифр получается путем применения одновременно операции сложения и умножения по модулю m над порядковыми номерами символов алфавита.

E(t)= at+b(mod m),

E(t) – порядковый номер символа алфавита на который происходит замена;

t – порядковый номер символа алфавита, который заменяется;

a, b – целые числа;

m – количество символов в алфавите.

 

t

3t+5

 

Преобразуя числа в буквы английского языка, получаем следующее соответствие для букв открытого текста и шифртекста:

 

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

F

I

L

O

R

U

X

A

D

G

J

M

P

S

V

Y

B

E

H

K

N

Q

T

W

Z

C

Шифрование методом Цезаря с ключевым словом.

Система шифрования Цезаря с ключевым словом является одноалфавитной системой подстановки. Особенностью этой системы является использование ключевого слова для смещения и изменения порядка символов в алфавите подстановки.

Выберем некоторое число k, 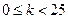, и слово или короткую фразу в качестве ключевого слова. Желательно, чтобы все буквы ключевого слова были различными. Пусть выбраны слово DIPLOMAT в качестве ключевого слова и число k=5.

Ключевое слово записывается под буквами алфавита, начиная с буквы, числовой код которой совпадает с выбранным числом k:

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

D

I

P

L

O

M

A

T

 

Оставшиеся буквы алфавита подстановки записываются после ключевого слова в алфавитном порядке:

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

V

W

X

Y

Z

D

I

P

L

O

M

A

T

B

C

E

F

G

H

J

K

N

Q

R

S

U

 

Теперь мы имеем подстановку для каждой буквы произвольного сообщения.

Исходное сообщение SEND MORE MONEY

шифруется как HZBY TCGZ TCBZS

Следует отметить, что требование о различии всех букв ключевого слова не обязательно. Можно просто записать ключевое слово (или фразу) без повторения одинаковых букв. Например, ключевая фраза

КАК ДЫМ ОТЕЧЕСТВА НАМ СЛАДОК И ПРИЯТЕН

и число k=3 порождают следующую таблицу подстановок:

А

Б

В

Г

Д

Е

Ж

З

И

Й

К

Л

М

Н

О

П

Р

С

Т

У

Ф

Х

Ц

Ч

Ш

Щ

Ь

Ы

Ъ

Э

Ю

Я

Ъ

Э

Ю

К

А

Д

Ы

М

О

Т

Е

Ч

С

В

Н

Л

И

П

Р

Я

Б

Г

Ж

З

Й

У

Ф

Х

Ц

Ш

Щ

Ь

 

Шифрование методом таблиц Трисемуса.

В этом шифре замены обычно используется таблица для записи букв алфавита и ключевое слово (или фраза). В таблицу сначала вписывалось по строкам ключевое слово, причем повторяющиеся буквы отбрасывались. Затем эта таблица дополнялась не вошедшими в нее буквами алфавита по порядку. Поскольку ключевое слово или фразу легко хранить в памяти, то такой подход упрощал процессы шифрования и расшифрования.

Например:

Для русского алфавита шифрующая таблица может иметь размер 4х8. Выберем в качестве ключа слово БАНДЕРОЛЬ. Шифрующая таблица с таким ключом:

Б	А	Н	Д	Е	Р	О	Л
Ь	В	Г	Ж	З	И	Й	К
М	П	С	Т	У	Ф	Х	Ц
Ч	Ш	Щ	Ы	Ъ	Э	Ю	Я

При шифровании находят в этой таблице очередную букву открытого текста и записывают в шифртекст букву, расположенную ниже ее в том же столбце. Если буква текста оказывается в нижней строке таблицы, тогда для шифртекста берут самую верхнюю букву из того же столбца.

При шифровании с помощью этой таблицы сообщения

ВЫЛЕТАЕМПЯТОГО

получаем шифртекст

ПДКЗЫВЗЧШЛЫЙСЙ.

Шифрование методом биграмного шифра Плейфейра.

Шифрующие таблицы позволяют шифровать сразу по две буквы. Такие шифры называют биграммными.

Основой шифра Плейфейра является шифрующая таблица со случайно расположенными буквами алфавита исходных сообщений.

Для удобства запоминания шифрующей таблицы можно использовать ключевое слово (или фразу) при заполнении начальных строк таблицы. В целом структура шифрующей таблицы системы Плейфейра полностью аналогична структуре шифрующей таблицы Трисемуса.

Процедура шифрования включает следующие шаги.

1. Открытый текст исходного сообщения разбивается на пары букв (биграммы). Текст должен иметь четное количество букв и в нем не должно быть биграмм, содержащих две одинаковые буквы. Если эти требования не выполнены, то текст модифицируется даже из-за незначительных орфографических ошибок.
2. Последовательность биграмм открытого текста преобразуется с помощью шифрующей таблицы в последовательность биграмм шифртекста по следующим правилам:
1. Если обе буквы биграммы открытого текста не попадают на одну строку или столбец (как, например, буквы А и Й в таблице Трисемуса), тогда находят буквы в углах прямоугольника, определяемого данной парой букв. (В нашем примере это – буквы АЙОВ. Пара букв АЙ отображается в пару ОВ. Последовательность букв в биграмме шифртекста должна быть зеркально расположенной по отношению к последовательности букв в биграмме открытого текста.)
2. Если обе буквы биграммы открытого текста принадлежат одному столбцу таблицы, то буквами шифртекста считаются буквы, которые лежат под ними. (Например, биграмма НС дает биграмму шифртекста ГЩ). Если при этом буква открытого текста находится в нижней строке, то для шифртекста берется соответствующая буква из верхней строки того же столбца. (Например, биграмма ВШ дает биграмму шифртекста ПА.)
3. Если обе буквы биграммы открытого текста принадлежат одной строке таблицы, то буквами шифртекста считаются буквы, которые лежат справа от них. (Например, биграмма НО дает биграмму шифртекста ДЛ.) Если при этом буква открытого текста находится в крайнем правом столбце, то для шифра берут соответствующую букву из левого столбца в той же строке. Например, биграмма ФЦ дает биграмму ширтекста ХМ.)

Зашифруем текст

ВСЕ ТАЙНОЕ СТАНЕТ ЯВНЫМ

Разбиение этого текста на биграммы дает

ВС ЕТ АЙ НО ЕС ТА НЕ ТЯ ВН ЫМ

Данная последовательность биграмм открытого текста преобразуется с помощью шифрующей таблицы в следующую последовательность биграмм шифртекста:

ГП ДУ ОВ ДЛ НУ ПД ДР ЦЫ ГА ЧТ

При расшифровании применяется обратный порядок действий.

Шифрование методом многоалфавитной одноконтурной обыкновенной подстановкой.

При полиалфавитной одноконтурной обыкновенной подстановке для замены символов исходного текста используется несколько алфавитов, причем смена алфавитов осуществляется последовательно и циклически, т.е. первый символ заменяется соответствующим символом первого алфавита, второй — символом второго алфавита и т.д. до тех пор, пока не будут использованы все выбранные алфавиты. После этого использование алфавитов повторяется.

В качестве примера рассмотрим шифрование с помощью таблицы Виженера. Таблица Виженера представляет собой матрицу с n² элементами, где n — количество символов используемого алфавита. Каждая строка матрицы получена циклическим сдвигом алфавита на символ. Для шифрования выбирается буквенный ключ, в соответствии с которым формируется рабочая матрица шифрования. Осуществляется это следующим образом. Из полной таблицы выбирается первая строка и те строки, первые буквы которых соответствуют буквам ключа. Первой размещается первая строка, а под нею — строки, соответствующие буквам ключа в порядке следования этих букв в ключе.

Сам процесс шифрования осуществляется следующим образом:

· под каждой буквой шифруемого текста записывают буквы ключа (ключ при этом повторяется необходимое количество раз);

· каждая буква шифруемого текста заменяется по подматрице буквами, находящимися на пересечении линий, соединяющих буквы шифруемого текста в первой строке подматрицы и находящихся под ними букв ключа;

· полученный текст может разбиваться на группы по несколько знаков.

Шифрование методом многоалфавитной одноконтурной монофонической подстановки.

Частным случаем рассмотренной многоалфавитной подстановки является так называемая монофоническая подстановка. Особенность этого метода состоит в том, что количество и состав алфавитов выбираются таким образом, чтобы частоты появления всех символов в зашифрованном тексте были одинаковыми. При таком положении затрудняется криптоанализ зашифрованного текста с помощью его статической обработки. Выравнивание частот появления символов достигается за счет того, что для часто встречающихся символов исходного текста предусматривается использование большего числа заменяющих элементов, чем для редко встречающихся.

Шифрование методом многоалфавитной многоконтурной подстановкой.

Многоалфавитная многоконтурная подстановка заключается в том, что для шифрования используется несколько наборов (контуров) алфавитов, используемых циклически, причем каждый контур в общем случае имеет свой индивидуальный период применения. Этот период исчисляется, как правило, количеством знаков, после зашифровки которых меняется контур алфавитов. Частным случаем многоконтурной многоалфавитной подстановки является замена по таблице Вижинера, если для шифрования используется несколько ключей, каждый из которых имеет свой период применения.

Шифрование методом «двойной квадрат» Уитстона.

Этот метод использует сразу две таблицы, размещенные по одной горизонтали, а шифрование идет биграммами, как в шифре Плейфейра.

Поясним процедуру шифрования этим шифром на примере. Пусть имеются две таблицы со случайно расположенными в них русскими алфавитами (рис. 2). Перед шифрованием исходное сообщение разбивают на биграммы. Каждая биграмма шифруется отдельно. Первую букву биграммы находят в левой таблице, а вторую букву – в правой таблице. Затем мысленно строят прямоугольник так чтобы буквы биграммы лежали в его противоположных вершинах. Другие две вершины этого прямоугольника дают буквы биграммы шифртекста.

Ж	Щ	Н	Ю	Р
И	Т	Ь	Ц	Б
Я	М	Е	.	С
В	Ы	П	Ч
:	Д	У	О	К
З	Э	Ф	Г	Ш
Х	А	,	Л	Ъ

 

И	Ч	Г	Я	Т
,	Ж	Ь	М	О
З	Ю	Р	В	Щ
Ц	:	П	Е	Л
Ъ	А	Н	.	Х
Э	К	С	Ш	Д
Б	Ф	У	Ы

Рис. 2 Две таблицы со случайно расположенными символами русского алфавита для шифра «двойной квадрат»

Предположим, что шифруется биграмма исходного текста ИЛ. Буква И находится в столбце 1 и строке 2 левой таблицы. Буква Л находится в столбце 5 и строке 4 правой таблицы. Это означает, что прямоугольник образован строками 2 и 4, а также столбцами 1 левой таблицы и 5 правой таблицы. Следовательно, в биграмму шифртекста входят буква О, расположенная в столбце 1 и строке 4 левой таблицы, т.е. получаем биграмму шифртекста ОВ.

Если обе буквы биграммы сообщения лежат в одной строке, то и буквы шифртекста берут из этой же строки. Первую букву биграммы шифртекста берут из левой таблицы в столбце, соответствующем второй букве биграммы сообщения. Вторая же буква биграммы шифртекста берется из правой таблицы в столбце, соответствующем первой букве биграммы сообщения. Поэтому биграмма сообщения ТО превращается в биграмму шифртекста ЖБ. Аналогичным образом шифруются биграммы сообщения:

Сообщение ПР ИЛ ЕТ АЮ _Ш ЕС ТО ГО

Шифртекст ПЕ ОВ ЩН ФМ ЕШ РФ БЖ ДЦ