. (1.13)
Дифференцируя вышестоящее выражение
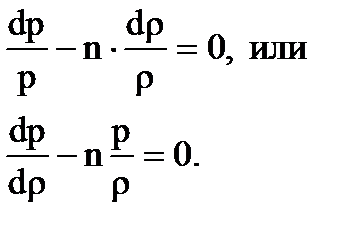(1.14)
Подставляя (1.13) в (1.14), получим
При адиабатном (изоэнтропном) процессе
,
где k – постоянная адиабаты, для воздуха равна 1,4.
Если учесть значения постоянных k и R для воздуха, а также уравнение состояния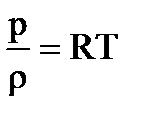 
, то при t =15°C, a =341 м/с.
.
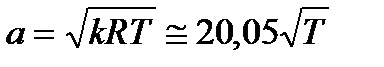Режим течения газа, при котором его местная скорость равна местной скорости звука (V=a,®М=1), называется критическим, а параметры, характеризующие течение 
критическими: 
(иногда в литературе встречаются обозначения pкр, rкр, Tкр).
Критический режим течения газа достигается в минимальном (узком) сечении сопла Лаваля (сужающе–расширяющегося сопла), а также при обтекании самолета и его частей (крыло, фюзеляж) в местах, где площадь сечения воздушных струек достигает наименьшего значения, вначале сужаясь, а потом расширяясь.
В качестве примера (рис. 1.5) можно рассмотреть обтекание струйками воздушного потока профиля крыла и реализацию критического режима на верхней поверхности профиля.
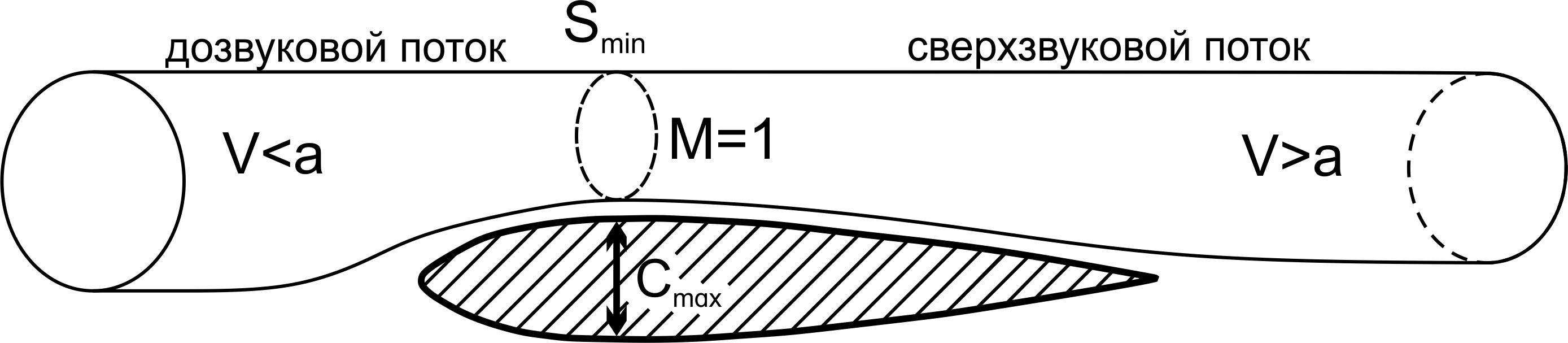
Рис. 1.5 Реализация критического режима на верхней поверхности профиля.
Если для анализа работы уравнения энергии выбрать сопло Лаваля, показанное на рис. 1.6, то скорость в его сужающейся (по направлению течения газа) части будет возрастать (работает уравнение расхода rVS=const). Значит статическая температура будет уменьшаться.
Скорость звука определяется формулой
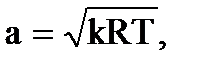
где R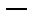 
удельная газовая постоянная и равна 287,2 
Следовательно, при уменьшении T скорость звука также будет уменьшаться. Таким образом, в области минимального сечения возможно равенство V=a, т.е. местные скорости газа и звука равны (М=1).
Критическую скорость можно определить
Рис.1.6 Течение газа в сопле Лаваля
или, используя ряд математических преобразований, получим
Из термодинамики известны соотношения между критическими параметрами и параметрами торможения (для изоэнтропного энергоизолированного или адиабатного течения)
.
Отсюда можем определить термодинамические параметры 
, 
и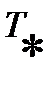 
в критическом сечении, зная параметры торможения.
Рассмотрим другие характерные скорости газа.
Число Маха 
изменяется в диапазоне от 0 до ¥.
Приведенная скорость или коэффициент скорости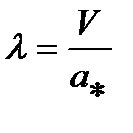 
изменяется от 0 до максимального значения 
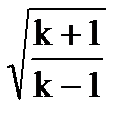»2,449 (для воздуха).
Если М=1, то и l=1.
Связь между М и l выражается формулой
Явление аэродинамического нагрева
В том случае, когда теплообмен между поверхностью ВС (например, стенкой кабины) и газом отсутствует, тепло выделившееся за счет трения (диссипации) в пограничном слое, нагревает газ. Образуется градиент температуры, направленный к стенке, и соответствующий ему тепловой поток, направленный от стенки.
Такой теплообмен для ламинарного пограничного слоя (ПС) осуществляется за счет теплопередачи (от слоя к слою), а для турбулентного пограничного слоя – за счет конвекции (переноса тепла вихрями).
Рассмотрим уравнение энергии для адиабатного течения, являющееся частным случаем уравнения закона сохранения энергии в газе, которое рассматривает переход из одного вида энергии (внутренней, кинетической, потенциальной при наличии теплообмена, совершения работы над газом и диссипации) в газе в другой
.
Проанализируем обтекание профиля крыла самолета потоком воздуха (рис. 1.7).
Известно, что в пограничном слое скорость потока изменяется от 0 на стенке до скорости невозмущенного потока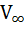 
на внешней границе пограничного слоя.
Анализ уравнения энергии показывает, что при уменьшении скорости в пограничном слое статическая температура должна возрастать от 
на внешней границе пограничного слоя до температуры торможения 
на поверхности крыла, где V=0.
Рис. 1.7 К вопросу аэродинамического нагрева ВС
Поскольку в пределах ПС по направлению к поверхности крыла температура возрастает, следует сделать вывод, что в направлении поверхности крыла действует тепловой поток, плотность которого определяется градиентом температуры по нормали к стенке
,
где q 
плотность теплового потока, 
;
dT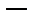 
приращение статической температуры;
n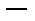 
нормаль к поверхности крыла.
Подобный нагрев газа за счет его торможения в пограничном слое называется аэродинамическим нагревом, а его величина зависит от скорости полета ВС.
Используя уравнение энергии и уравнение Бернулли для сжимаемого течения, можно определить температуру в любой точке крыла.
Для расчета обычно используют приближенную формулу
где 
скоростная доставка к статической температуре газа, град.
Варьируя значение числа М, можно получить значения прироста температуры в зависимости от скорости для условий по стандартной атмосфере (СА).
Пример. В полете со скоростью 900 км/ч (250 м/с) воздух за счет торможения в ПС нагревается примерно на 31,5° С. На высоте 10 000м, где температура составляет порядка минус 50° С, это не представляет проблемы. Но при полете у земли с такой скоростью аэродинамический нагрев становится весьма ощутимым.
Аэродинамический нагрев актуален для воздушно-космических самолетов (типа ВКС «Буран» или «Space Shuttle»), у которых на этапе входа в атмосферу необходимы специальные методы охлаждения кабин.
Для магистральных ВС экипажу следует считаться с эффектом аэродинамического нагрева при полете в условиях обледенения. Вследствие торможения на передней части крыла возникает зона относительно высоких температур. А уже, начиная со средней части крыла и далее, образуется зона обледенения (барьерный лед).
