В реляционной БД отношение между объектами (сущностями) определяет связи между таблицами. Поддерживаются связи четырех типов: «один к одному», «один ко многим», «много к одному» и «многие ко многим». Рассмотрим подробнее типы связей в применении к реляционной модели данных:
· «один к одному»
Отношение «один к одному» означает, кто каждой записи из первой таблицы соответствует одна и только одна запись из другой таблицы. Рассмотрим таблицы, содержащие персональные и служебные сведения о работниках некоторой фирмы.


Персональные сведения
| Код_пс | № паспорта | Фамилия | Имя |
| AB 2358955 | Сидоров | Сергей | |
| DB 2456886 | Петров | Петр | |
| MA 8654212 | Иванов | Иван |
Служебные сведения
| Код_сс | Место работы | Должность | Разряд |
| Бухгалтерия | Бухгалтер | ||
| Цех 2 | Токарь | ||
| Лабаратория 3 | Начальник отдела |
Между таблицами «Персональные сведения» и «Служебные сведения» существует отношение «один к одному», поскольку для одного человека, работающего в определенной фирме, может существовать только одна запись о его служебном положении. Табельные номера «Код_пс» и «Код_сс» были добавлены для однозначной идентификации записей. Эти же поля и приняты в качестве первичных ключей. Связь между этими таблицами поддерживается при помощи совпадающих значений полей «Код_пс» и «Код_сс». Легко убедиться, что между двумя ключевыми полями может существовать только связь «один к одному», поскольку любые дублирования одного и того же табельного номера исключены с обеих сторон.
· «один ко многим» и «много к одному»
Отношение «один ко многим» означает, что каждой записи из первой таблицы может соответствовать одна либо много записей из другой таблицы.
Рассмотрим таблицы, содержащие сведения о клиентах некоторой фирмы и сделанных ими заказах.
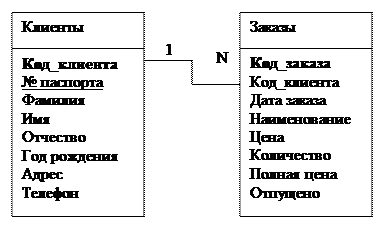

Клиенты
| Код_клиента | № паспорта | Фамилия | Имя |
| AB 2358955 | Сидоров | Сергей | |
| DB 2456886 | Петров | Петр | |
| MA 8654212 | Иванов | Иван |
Заказы
| Код_заказа | Код_клиента | Дата заказа | Наименование |
| 05.03.06 | Пылесос Вихрь | ||
| 15.04.06 | Холодильник Минск | ||
| 21.04.06 | Телевизор Горизонт | ||
| 02.10.06 | Стол компьютерный | ||
| 12.12.06 | Кресло «Президент» |
Предполагается, что один и тот же покупатель может сделать несколько заказов. Таким образом, между этими таблицами существует связь «один ко многим». Для установления связи необходимо в таблицу «Заказы» ввести поле «Код_клиента». Связь между таблицами будет осуществляться на основании значений совпадающих полей «Код_клиента». Причем подчеркнем, что связь устанавливается на основе значений совпадающих полей, а не их наименований. Таким образом, если связь устанавливается между ключевым полем одной таблицы и неключевым полем второй таблицы, то это будет связь типа «один ко многим».
· «много ко многим»
Отношение «много ко многим» возникает между двумя таблицами в тех случаях, когда:
- каждой записи из первой таблицы может соответствовать одна либо много записей из другой таблицы,
- одной записи из второй таблицы может соответствовать одна либо много записей из первой таблицы.
Типичным примером является связь между клиентами некой фирмы и покупаемыми ими товарами. Каждый товар может быть куплен несколькими клиентами и наоборот, один клиент может купить несколько товаров. Такая связь может быть реализована с помощью дополнительной таблицы, содержащей ключевые поля обеих таблиц, участвующих в связи.


Клиенты
| Код_клиента | № паспорта | Фамилия | Имя |
| AB 2358955 | Сидоров | Сергей | |
| DB 2456886 | Петров | Петр | |
| MA 8654212 | Иванов | Иван |
Товары
| Код_товара | Наименование | Цена |
| Пылесос Вихрь | ||
| Холодильник Минск | ||
| Телевизор Горизонт |
Заказы
| Код_заказа | Код_клиента | Код_товара | Дата заказа |
| 05.03.2006 | |||
| 15.04.2006 | |||
| 21.04.2006 | |||
| 02.10.2006 | |||
| 12.12.2006 | |||
| 30.12.2006 | |||
| 31.12.2006 |
Связь «много ко многим» также автоматически возникает между таблицами, связанными посредством неключевых полей. Пусть первая таблица содержит информацию о том, на каких станках могут работать рабочие некоторой бригады. Вторая таблица содержит сведения о том, кто из бригады ремонтников какие станки обслуживает.
Таблица 1 Таблица 2
| Работает | Станок |
| Иванов А. В. | станок 1 |
| Иванов А.В. | станок 2 |
| Петров Н.Г. | станок 1 |
| Петров Н.Г. | станок З |
| Сидоров В. К. | станок 2 |
| Обслуживает | Станок |
| Голубев Б. С. | станок 1 |
| Голубев Б. С. | станок 2 |
| Зыков А.Ф. | станок 2 |
| Зыков А.Ф. | станок З |
Первой и третьей записям таблицы 1 соответствует первая запись таблицы 2. Четвертой записи таблицы 1 соответствуют вторая и четвертая записи таблицы 2. Такой вид связи М:N характеризуется как слабый вид связи или даже как отсутствие связи, поскольку никакого контроля за целостностью данных в этом случае не производится.
Информация, размещенная в связанных таблицах, может быть легко объединена с помощью запросов объединения. Для нашего примера будем иметь
Заказы
| Фамилия | Имя | Наименование | Цена | Дата заказа |
| Сидоров | Сергей | Пылесос Вихрь | 05.03.2000 | |
| Петров | Петр | Холодильник Минск | 15.04.2000 | |
| Петров | Петр | Телевизор Горизонт | 21.04.2000 | |
| Сидоров | Сергей | Электрочайник BOSCH | 02.10.2000 | |
| Иванов | Иван | Пылесос Вихрь | 12.12.2000 | |
| Иванов | Иван | Телевизор Горизонт ТЦ | 30.12.2000 | |
| Сидоров | Сергей | Холодильник Минск | 31.12.2000 |
Целостноть реляционной БД
Рассмотрим подробнее ограничители целостности в применении к реляционной модели данных. Понятие ссылочной целостности неразрывно связано с понятием внешних ключей и формулируется для реляционной БД следующим образом. Реляционная БД не должна содержать несогласованных значений внешних ключей, т.е. таких значений, для которых не существует отвечающих им значений соответствующих потенциальных ключей базовых таблиц. Иначе говоря, внешние ключи могут содержать только те значения, которые принимают соответствующие им ключевые поля базовых таблиц. Если в БД уже есть клиент с номером 10 и товар с номером 25, то только тогда можно внести запись о покупке клиентом 10 товара 25 в таблицу “Заказы”. С другой стороны нельзя удалить клиента с номером 25, или даже изменить его номер, если в БД хранится хотя бы одна запись о сделанном им заказе. В противном случае согласованность внешних ключей тоже нарушается, так как запись в таблице “Заказы” будет содержать значение, указывающее на несуществующего клиента.
Есть два правила внешних ключей, обеспечивающих согласованное состояние БД. Первое заключается в ограничении обновления и удаления. При работе с базовой таблицей это правило запрещает удаление записей, которые содержат связанные записи в подчиненных таблицах и изменение значений их первичных ключей. При работе с подчиненной таблицей это правило запрещает установку внешнего ключа в значение, которого не существует для соответствующего потенциального ключа базовой таблицы. Второе из них заключается в каскадном обновлении и каскадном удалении записей подчиненных таблиц при операциях с базовой таблицей. При изменении значения базового ключа, использующегося в связи, все значения внешних ключей всех подчиненных таблиц должны быть изменены соответственно (каскадное обновление). При удалении записи из базовой таблицы все связанные с ней записи из подчиненных таблиц должны быть также удалены (каскадное удаление). Если для внешних ключей разрешены Null значения, то в некоторых реляционных СУБД вместо каскадного удаления может применяться операция Nullify, которая устанавливает внешние ключи подчиненных таблиц в Null при удалении соответствующего значения базового ключа.
Кроме ссылочной целостности можно сформулировать еще три ограничителя целостности для реляционной БД:
· Ограничители домена (domain constraints), запрещающие ввод значений атрибутов, не принадлежащих домену. К ним можно отнести также все ограничители значений (тип, формат, задание списка и диапазона значений);
· Ограничители ключей (key constraints), обеспечивающие уникальность значений потенциальных ключей (обеспечивается применением уникальных индексов);
· Ограничители записи (entity constraints), запрещающие Null значения для первичных ключей, так как в противном случае будет нарушено требование идентифицируемости записи.
Реляционная алгебра
Реляционная алгебра представляет собой совокупность операций высокого уровня над отношениями. Эти операции можно разделить на две группы:
a) пять основных операций - ОБЪЕДИНЕНИЕ, РАЗНОСТЬ, ДЕКАРТОВО ПРОИЗВЕДЕНИЕ, ПРОЕКЦИЯ, ВЫБОР;
b) дополнительные операции не расширяющие возможности основных операций, однако, обеспечивающие краткость записи, - ПЕРЕСЕЧЕНИЕ, СОЕДИНЕНИЕ, СЛИЯНИЕ, ДЕЛЕНИЕ.
Операндами операций реляционной алгебры являются постоянные и (или) переменные отношения. Для операций объединение, разность и пересечение оба участвующих в них отношения должны быть:
Совместимы по объединению (т. е. иметь одинаковую арность и атрибуты, по которым осуществляется операция), определены на одном домене.
Рассмотрим названные операции на примерах отношений R и S:
| R | (A | B | C) | S | (D | E | F) | ||||||
| p | 1 | a | p | 2 | b | ||||||||
| p | 2 | b | p | 3 | a | ||||||||
| p | 2 | c |
Основные операции. Операцией ОБЪЕДИНЕНИЕ отношений R и S называется отношение Т=R  S, включающее множество кортежей, принадлежащих R или S или им обоим. Все кортежи результатного отношения Т имеют одинаковое число компонентов, поскольку операция применяется к отношениям одной и той же арности.
S, включающее множество кортежей, принадлежащих R или S или им обоим. Все кортежи результатного отношения Т имеют одинаковое число компонентов, поскольку операция применяется к отношениям одной и той же арности.
Пример 2.8. Операция ОБЪЕДИНЕНИЕ имеет вид
R  S S
| p | 1 | a |
| p | 2 | b | |
| q | 2 | c | |
| q | 3 | a |
Операцией РАЗНОСТЬ отношений R и S, определенных на общем домене, называется отношение Т=R-S, включающее множество кортежей, принадлежащих R, но не принадлежащих S. Отношения R и S имеют одинаковую арность.
Пример 2.9: Операция РАЗНОСТЬ имеет вид:
| R - S | p | 1 | a |
| q | 2 | c |
Операция ДЕКАРТОВО ПРОИЗВЕДЕНИЕ отношений R и S, которые соответственно имеют арности К1 и К2, называется отношение Т=R×S,включающее множество кортежей длиной К1+К2, первые К1 компонентов которых образуют кортежи, принадлежащие R, а последние К2- кортежи, принадлежащие S. Другими словами, производится конкатенация кортежей из отношений R и S.
Пример 2.10. Операция ДЕКАРТОВО ПРОИЗВЕДЕНИЕ имеет вид
| R х S | (A | B | C | D | E | F) | |||
| p | 1 | a | p | 2 | b | ||||
| p | 1 | a | q | 3 | a | ||||
| p | 2 | b | p | 2 | p | ||||
| p | 2 | b | q | 3 | a | ||||
| q | 2 | c | p | 2 | b | ||||
| q | 2 | c | q | 3 | a |
Пусть t - кортеж отношения R(X) и А – атрибут Х, тогда t[А] - А -компонента кортежа t. Аналогично, если Y - подмножество Х, t[Y] - кортеж (размерности ׀ Y ׀), который содержит компоненты t, соответствующие элементам Y.
Операцией ПРОЕКЦИЯ R на Y называется отношение R[Y], которое является вертикальным подмножеством столбцов отношения R:
R[Y]={t[Y]|t Є R}
Таким образом, R[Y]- отношение на Y, включающее все кортежи, получаемые из кортежей путем отбора компонентов, соответствующих Y, и удаления одинаковых кортежей (кроме одного) из множества, полученного в результате проектирования.
Другое обозначение для операции проекция πх(R).
Пример 2.11. Операция ПРОЕКЦИЯ имеет вид
R[A C] (A C) S[E F] (E F)
p a 2 b
p b 3 a
q c
Операция ВЫБОР строит горизонтальное подмножество кортежей отношения R, удовлетворяющих определенному предикату. Пусть Θ - одна из бинарных операций «<», «≤», «>», «≥», «=», «≠», применяемая к атрибуту (атрибутам) А и кортежу t. Тогда R[AΘt] - это набор кортежей отношения, каждая А -компонента которых находится в отношении Θ к кортежу t. Вместо кортежа t можно взять множество кортежей В таких, что А и В определяются на общих доменах. Тогда R[AΘB] - это набор кортежей отношения, А -компоненты которых находятся в отношении Θ к В -компонентам.
Пример 2.12. Операция ВЫБОР имеет вид
| R[С≠b] | (A | B | C) | R[A≠q ^ B>1] | (A | B | C) | |
| p | 1 | a | p | 2 | b | |||
| q | 2 | c |
Другим обозначением операции ВЫБОР является σAΘt (R).
Операцией ПЕРЕСЕЧЕНИЕ отношений R и S называется отношение T=R∩S, которое включает кортежи, принадлежащие как R, так и S. Другими словами, R∩S=R-(R-S).
Пример 2.13. Операция ПЕРЕСЕЧЕНИЕ имеет вид
R∩S p 2 b
Пусть R(X, Y) и S(Y, Z) – отношения, где X, Y, Z – непересекающиеся множества атрибутов и Y -множество атрибутов, общее для отношений R и S.
Операцией соединение отношений R и S называется отношение Т (X, Y, Z), определяемое как Т (X, Y, Z)={(х, y, z,)| (х, y) Є S}. Таким образом, отношение Т - это множество кортежей отношений R и S, имеющих одинаковые значения общих атрибутов для этих отношений.
Можно определить операцию СОЕДИНЕНИЕ более широко с точки зрения типа отношения между атрибутами отношений R и S. Пусть даны отношения R(A, B1) S(B2, C), где B1 и B2 определены на общем домене; Θ - одна из бинарных операций «<», «≤», «>», «≥», «=», «≠», в которых могут находиться атрибуты B1 и B2. Операция СОЕДИНЕНИЕ R по B1 и S по B2 (обозначается R[B1ΘB2] S) есть соединение кортежей из отношений R и S, атрибуты которых находятся в отношении Θ.
Пример 2.14. Операция СОЕДИНЕНИЕ имеет вид
| R[A=D] S | (A | B | C | D | E | F) |
| p | a | p | b | |||
| p | b | p | b | |||
| q | c | q | a | |||
R[B≤E  C=F] S C=F] S
| (A | B | C | D | E | F) |
| p | a | q | a | |||
| p | b | p | b | |||
Заметим, что отношения R и S могут иметь одинаковые имена атрибутов, и поэтому имена результатного отношения должны быть определены. Например, для отношений R(A, B) и S(A, B), где А и В определены на общем домене, можно задать следующую операцию СОЕДИНЕНИЕ:
Т(D, E, F, G)=R(A,B) [B>B] S(A, B).
Источником значений для атрибута D в T является атрибут А в R. Аналогично для атрибутов E, F, G и T источниками будут атрибуты B в R, A и S.
Операция СЛИЯНИЕ (естественное соединение) выполняется так же, как СОЕДИНЕНИЕ, при использовании операции «=» между атрибутами или множествами атрибутов отношений; при этом в результатном отношений удаляются одинаковые столбцы. Применим операцию СЛИЯНИЕ для примера 8.
Пример 2.15. Операция СЛИЯНИ Е имеет вид
| R[A*D] S | (A | B | C | E | F) |
| p | a | b | |||
| p | b | b | |||
| q | c | a |
Операция СЛИЯНИЕ может быть также обозначен R  S.
S.
Операция ДЕЛЕНИЕ определяется следующим образом. Пусть даны отношения R(A, B) и P(C), где атрибуты B и C определены на одном домене. Тогда R[B÷C] P – подмножество R[A] (частное), которое получается в результате деления значений атрибута С и S (делитель), т.е. если отношение R и P имеют соответственно арность r и p, где r>p; p ≠0. Тогда R÷ P - множество кортежей t длиной r – p таких, что для всех кортежей длиною p, принадлежащих P, кортеж t принадлежит R. Заметим, что декартово произведение R[А] с Р[С] принадлежит отношению R.
Пример 2.16. Пусть задано отношение Р:
Р (В С)
1 a
2 c
Тогда операция ДЕЛЕНИЕ имеет вид
R÷Р(А)
р
q
Постреляционная модель
Классическая реляционная модель предполагает неделимость данных, хранящихся в полях записей таблиц. Существует ряд случаев, когда это ограничение мешает эффективной реализации приложений.
Постреляционная модель данных представляет собой расширенную реляционную модель, снимающую ограничение неделимости данных, хранящихся в ячейках таблицы. Поскольку атомарность данных постулируется первой нормальной формой, то исходя из этого определения, ее называют также непервой нормальной формой (Non-First Normal Form - NFNF или NF2) реляционной моделью. Постреляционная модель данных допускает многозначные и составные поля. Набор значений многозначных полей считается самостоятельной таблицей, встроенной в основную таблицу. Вследствие этого ее еще часто называют вложенной (Nested) реляционной моделью. Все атрибуты в постреляционной модели рассматриваются как составные, имеющие иерархическую структуру, причем на количество ветвей не накладывается каких либо ограничений. Это позволяет на одном уровне иерархии хранить целые массивы данных.
| ID | Имя | Адрес | Тел | |||||||
| Фамилия | Имя | Отчество | Страна | Город | Доп. адрес | Номер | Тип | |||
| Улица | Д. | Кв. | ||||||||
| Сидоров | Петр | Петрович | Беларусь | Минск | Пушкина | Дом. | ||||
| Толстого | Раб. | |||||||||
| (029)6257533 | Моб. | |||||||||
| Иванов | Иван | Иванович | Беларусь | Гродно | Ленина | Дом. | ||||
| Литва | Вильнюс | Лесная | Дом. |
По сравнению с реляционной в постреляционной модели данные хранятся более эффективно, а при обработке не требуется выполнять операцию соединения данных из двух и более таблиц. Помимо обеспечения вложенности полей постреляционная модель поддерживает ассоциированные многозначные поля (множественные группы). Совокупность ассоциированных полей называется ассоциацией. При этом в некоторой строке первое значение одного столбца ассоциации соответствует первым значениям всех остальных столбцов ассоциации. Аналогичным образом связаны все вторые значения столбцов и т. д. На длину полей и количество полей в записях таблицы не накладывается требование постоянства. Это означает, что структура данных и таблиц имеет большую гибкость. Но поскольку постреляционная модель допускает хранение в таблицах ненормализованных данных, возникает проблема обеспечения целостности и непротиворечивости данных. Эта проблема решается с помощью процедур, автоматически выполняемых до или после обращения к данным.
Достоинством постреляционной модели является возможность представления совокупности связанных реляционных таблиц одной постреляционной таблицей. Это обеспечивает высокую наглядность представления информации и повышение эффективности ее обработки. Недостатком постреляционной модели является сложность решения проблемы обеспечения целостности и непротиворечивости хранимых данных. Эта модель пока не реализована в полном объеме в коммерческих СУБД. Примером использования некоторых концепций этой модели может служить система Oracle 8. В этой СУБД реализована поддержка составных и многозначных атрибутов, а также вложенных таблиц (Nested Tables). Для хранения составных атрибутов в Oracle 8 используется тип данных OBJECT. Например:
CREATE TYPE Tel_Type AS OBJECT(Tel_Number CHAR(10), Tel_Descr CHAR(5));
Для хранения многозначных атрибутов используется тип данных VARRAY, представляющий собой массив некоторых объектов переменной длины, имеющий два свойства: (1) Count – число элементов в массиве и (2) Limit – максимальное число элементов в массиве (задается при определении этого типа). Для формирования массива объектов вначале требуется определить тип объектов, которые будут храниться в массиве, например:
CREATE TYPE Tel_Type AS OBJECT(Tel_Number CHAR(10), Tel_Descr CHAR(5));
CREATE TYPE Tel_List_Type AS VARRAY(5) OF Tel_Type;
Этот же набор данных можно определить и как вложенную таблицу (Nested Tables).
CREATE TYPE Tel_List_Type AS TABLE OF Tel_Type;
Оба объекта VARRAY и TABLE имеют похожие свойства, но имеют и существенные различия. Во первых, тип VARRAY имеет верхний предел число элементов, а TABLE – не имеет. Во вторых, во вложенных таблицах можно обращаться к отдельным ее элементам и дополнительно определять индексы, что не допустимо в VARRAY.
Многомерная модель
Многомерный подход к представлению данных в базе появился практически одновременно с реляционным, но реально работающих многомерных СУБД (МСУБД) до настоящего времени было очень мало. С середины 90-х годов с развитием систем OLAP (On Line Analytical Processing — оперативная аналитическая обработка данных), Data Warehousing и Data Mining (применяющихся для сложного анализа данных, принятия решений, менеджмента и получения новых знаний) интерес к ним стал приобретать массовый характер. Основное назначение OLAP систем заключается в динамическом синтезе, анализе и консолидации больших объемов многомерных данных, а это, в свою очередь, связано с необходимостью извлекать большое количество записей из больших БД и производить их оперативную обработку (например, быстро вычислять итоговые значения). Кратко определить Data Warehousing можно как предметно (проблемно) ориентированную, интегрированную, постоянную в структуре, но зависящую от времени совокупность данных, предназначенных для принятия некоторых решений. Главное ее отличие от стандартных баз данных состоит в том, что она представляется собранием данных из многих баз данных, объединенных вместе для решения какой-либо частной задачи, либо является построенной по определенным правилам выборкой из очень большой базы данных. Существенным ее отличием можно считать также отсутствие операций обновления данных.
Data Mining (добыча данных) также является системой, основанной на данных, главная задача которой состоит в исследовании данных с целью получения новых знаний. Эта система применяется преимущественно не для выборки данных и представления их в определенной форме, а для сложного анализа данных, как например, поиск цепочек ДНК и т. д. Data Mining преследует следующие цели:
предсказание (например, прогноз погоды, устойчивость развития экономики);
идентификация (по образцу, …);
классификация;
оптимизация (создание более оптимально действующих систем на основе анализа уже существующих).
Многомерные СУБД являются узкоспециализированными СУБД, предназначенными для интерактивной аналитической обработки информации. Многомерность модели данных в них означает не многомерность визуализации цифровых данных, а многомерное логическое представление структуры информации при описании и в операциях манипулирования данными. При этом зачастую создается только многомерное логическое представление данных, а не их хранение. То есть сами данные могут храниться в больших БД, например, реляционных, а в требуемый момент времени извлекаться оттуда. Обычно в этом случае доступ производится с помощью многомерных индексов. Поскольку многомерные модели предназначены в основном для аналитической обработки данных, а не для создания удобных хранилищ информации, основные задачи в них реализуются операциями консолидации, выполняющие расчет всех промежуточных и основных итоговых значений, причем по всем размерностям. Это позволяет в много раз уменьшить объем представляемой информации и значительно ускорить доступ к данным и их последующую обработку. Такое предварительное обобщение является особенно ценным при работе с иерархически связанной информацией, например, при работе с данными, зависящими от времени.
По сравнению с реляционной моделью многомерная модель данных обладает более высокой скоростью доступа к данным, наглядностью и информативностью. Для сравнения ниже приведены реляционное (таблица 1) и многомерное (таблица 2) представления одних и тех же данных о продаже товаров:
Таблица 1. Реляционное представление данных
| Клиент | Товар | Цена | Количество | Дата |
| Иванов | Масло | 1000,00 | 02.02.2005 | |
| Петров | Молоко | 400,00 | 02.02.2005 | |
| Иванов | Сметана | 750,00 | 06.02.2005 | |
| Иванов | Масло | 1000,00 | 22.02.2005 | |
| Петров | Молоко | 400,00 | 03.03.2005 | |
| Сидоров | Масло | 1000,00 | 02.03.2005 | |
| Иванов | Сметана | 1500,00 | 12.03.2005 | |
| Иванов | Молоко | 500,00 | 05.04.2005 | |
| Сидоров | Сметана | 800,00 | 14.04.2005 | |
| Петров | Масло | 1200,00 | 28.04.2005 |
Таблица 2. Многомерное представление данных
| Дата Товар | Июнь 2005 | Июль 2005 | Август 2005 |
| Масло | |||
| Молоко | |||
| Сметана |

Рис. 2.13. Пример трехмерной модели таблиц, вычисляются по заранее заданным формулам)
Консолидация включает в себя простые обобщающие операции типа расчета итоговых значений, матричную арифметику, а также расчет сложных выражений;
Срез (Slice) представляет собой подмножество гиперкуба, полученное в результате фиксации одного или нескольких размерностей. Формирование среза выполняется, если размерностей всего две (таблица 2), то такое представление называется перекрестной или сводной таблицей. Объем продаж вычисляется на основе группированного представления продаж по товарам, клиентам и месяцам. На Рис. 2.13 показан пример трехмерной модели данных, где введена еще одна размерность Клиент. Если число размерностей велико, то информация не обязательно должна представляться визуально в виде каких-то многомерных объектов (n -мерных гиперкубов), тем более, что это не представляется возможным. Пользователь привык иметь дело с двумерными таблицами, диаграммами, графиками. Многомерная модель как раз предоставляет расширенный набор средств для выборки данных из многомерного хранилища данных, выполненных с разной степенью детализации.
Основными понятиями многомерных моделей являются измерение и ячейка, а операциями – консолидация, формирование среза, вращение, агрегация и детализация:
Размерность (Dimension) – это множество однотипных данных, образующих одну из граней гиперкуба. В многомерной модели данных размерности играют роль индексов, служащих для идентификации конкретных значений в ячейках гиперкуба;
Ячейка (Cell) или показатель – это поле, значение которого однозначно определяется фиксированным набором размерности. В зависимости от того, как формируются значения некоторой ячейки, обычно она может быть переменной (значения изменяются и могут быть загружены из внешнего источника данных или сформированы программно) либо формулой (значения, подобно формульным ячейкам электронных для ограничения выборки данных, поскольку все значения гиперкуба очень трудно представить визуально.
Вращение (Rotate) заключается в изменении порядка измерений при визуальном представлении данных.
Агрегация (Drill Up) и Детализация (Drill Down) означают соответственно переход к более общему и к более детальному представлению информации пользователю из гиперкуба. Например, в БД хранится информация о дате продажи товара. Тогда с помощью операции детализации можно уточнить момент продажи, а с помощью операции агрегации представить суммарную информацию по месяцам, кварталам и годам. Основным достоинством многомерной модели данных является удобство и эффективность аналитической обработки больших объемов данных, связанных со временем. При организации обработки аналогичных данных на основе реляционной модели происходит нелинейный рост трудоемкости операций в зависимости от размерности БД и существенное увеличение затрат оперативной памяти на индексацию. Недостатком многомерной модели данных является ее громоздкость для простейших задач обычной оперативной обработки информации.
Примерами систем, поддерживающими многомерные модели данных, являются Essbase (Arbor Software), Media Multi-matrix (Speedware), Oracle Express Server (Oracle), Cache (Inter Systems). В последней СУБД, основанной на многомерной модели данных, реализованы три способа доступа к данным: прямой (на уровне узлов многомерных массивов), объектный и реляционный.






