Анализ медико-биологических данных на основе числовых статистических характеристик

Кроме графического способа для описания случайных величин используется целый ряд числовых статистических характеристик. Условно их можно разделить на характеристики положения и характеристики разброса. Если эти характеристики определены по выборке, то они называются выборочными. Необходимо помнить, что выборочные характеристики являются лишь оценкой (приближением) генеральных характеристик, т.е. отражают их с некоторой ошибкой. Учитывая, что в основном, исследователь имеет дело с выборкой, в дальнейшем мы будем опускать слово «выборочный».

Пусть имеется случайная величина X (x₁, x₂, x₃ …..x_i……x_n)

К характеристикам положения относятся

Среднее значение (выборочная средняя обозначается как , генеральная средняя - буквой μ )

(1)

Среднее значение показывает, где на числовой оси располагается изучаемая совокупность, другими словами это некоторое значение случайной величины, возле которого группируются все другие. Из рисунка 8 видно, что первая совокупность группируется около значения 184,1 см, вторая – вокруг значения 165,5 см. По числовой оси вторая группа расположена ниже, чем первая.

Рисунок 8. Две выборки с различными средними значениями

Медиана (Ме) – это значение случайной величины, которое делит ранжированную выборку на две равные части. Если число объектов выборки четное, то медиана равна среднему двух соседних центральных значений. Половина объектов выборки имеет значение меньше медианы, половина – больше медианы.

Пример. Сопоставим возраст женщин-первородок за 2001 и 2010 годы. Выборочные исследования дали следующие результаты Таблица 4. Данные по женщинам-первородкам

год

Возраст женщин-первородок, лет

В первой выборке Ме = 23 года, во второй – Ме = 27 лет. Вывод: если в 2001 году половина женщин рожала впервые до 23 лет, то в 2010 году стали рожать позже – до 27 лет.

Мода (Мо) – наиболее часто встречающееся значение случайной величины. Для того, чтобы определить моду все значения выборки выстраиваются в ранжированный ряд (по возрастанию или по убыванию). Может быть несколько значений моды, может ее и не быть.

Мы уже упоминали о том, что одних средних значений недостаточно для описания групповых свойств. Такой случай представлен на рисунке 9. При равенстве средних значений состав этих совокупностей значительно разница – если члены первой группы все одинаковые по росту, то во второй встречаются низкорослые, среднего роста и высокие – т.е. здесь больше разброс изучаемого признака.

Рисунок 9. Две выборки с различными дисперсиями

К характеристикам разброса (рассеяния) относятся

Дисперсия (D)

(2)

Чем больше дисперсия, тем больше разброс данных, однако, это не просто разница между минимальным и максимальным значениями. В случае, который представлен на рисунке 10, размах (от min до max) в обеих выборках одинаков, но вторая дисперсия больше первой, поскольку, как видно из формулы, при вычислении дисперсии учитывается отклонение каждой величины от среднего значения.

Рисунок 10.

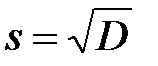
Если рост измеряется в см, то дисперсия измеряется в см², т.е. сама случайная величина и ее разброс выражены в различных единицах измерения, что не очень понятно, и не удобно. Поэтому была введена еще одна характеристика, которая позволяет избавиться от квадрата единицы измерения. Это среднеквадратическое отклонение или ее еще называют стандартным отклонением (посчитанное по выборке обозначается как s, генеральное значение - буквой σ)

(3)

Коэффициент вариации представляет собой относительную меру разброса, выраженную в процентах V% (иногда обозначается C_v)

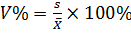(4)

Коэффициент вариации используют для сравнения разброса двух и более признаков, имеющих различные единицы измерения. Он позволяет судить об однородности совокупности: считаем выборку однородной при V% ≤ 33%. Однако это правило не всегда приемлемо, например нормальные значения в крови фосфатазы щелочной: 30-120 Ед/л. – т.е. может быть достаточно большой разброс.

Пример. В таблице 5 приведены результаты расчета статистических характеристик роста по группе взрослых и детей. Дисперсия по абсолютной величине выше у взрослых, но это связано с тем, что и рост у них значительно выше. Если же судить по коэффициенту вариации (по относительной величине), то у детей разброс в росте больше. Таблица 5. Рост взрослых и детей

	, см	D, см²	s, см	V%
рост взрослых		56,4	7,5	4,2
рост детей			4,9	7,4

Пример. При анализе состава работников промышленного предприятия были получены следующие данные.

Таблица 6. Состав работников предприятия

признак		s	V%
Стаж (лет)	8,7	2,8	32,1
Возраст (лет)	37,2	4,1	11,0
Образование (классов)	9,2	1,1	11,9

Согласно коэффициенту вариации коллектив относительно однороден по возрасту и образовательному уровню, однако не устойчив, поскольку отмечается большой разброс в стаже работы.

Минимальное значение , максимальное значение и размах

Нижний квартиль Q₂₅ – это значение случайной величины, ниже которого находится 25% выборки.

В ранжированном ряду нижний квартиль находится под номером, определяемым по формуле:

(округлить до ближайшего целого) (5)

Верхний квартиль Q₇₅ – это значение случайной величины, выше которого находится 25% выборки.

В ранжированном ряду верхний квартиль находится под номером, определяемым по формуле:

(округлить до ближайшего целого) (6)

Если номер квартиля получился дробным, то его можно округлить до ближайшего целого.

Межквартильный (интерквартильный) размах ΔQ=Q₇₅- Q₂₅. (7)

50 % данных лежит в пределах от нижнего до верхнего квартилей.

Еще одно понятие, которое мы должны ввести, это стандартная ошибка среднего. Так как среднее значение, как правило, определяется по ограниченной выборке, то оно отличается от истинной (генеральной) средней, то есть имеет определенную ошибку. Если вычислить средние по многим выборкам и усреднить их стандартные отклонения от генеральной средней мы и получим эту величину, которая обозначается буквой m и вычисляется по формуле

(8)

Статистические характеристики удобно отображать с помощью графика «ящик с усами» (whiskers box).

При анализе таких графиков обязательно надо обратить внимание на «легенду» - условные обозначение, которые приводятся в нижней части графика (рисунок 11). Если на первом графике (11А) приведены минимальное, максимальное, среднее значения и стандартное отклонение, то из второго графика (11Б) мы получаем информацию о медиане и квартилях.

А	Б

Рисунок 11. График «whiskers box»

Рассмотрим примеры практического использования перечисленных характеристик и убедимся, что они реально помогают оценивать ситуацию, когда анализируются большие по объему и разнообразные по свойствам совокупности.

Пример. Было проведено скрининговое исследование содержание глюкозы в крови мужчин возраста 45-60 лет. Известно, что норма составляет 3,55-5,55 ммоль/л. Необходимо сделать выводы по результатам, приведенным в таблице 7. Таблица 7. Статистические данные по содержанию глюкозы

(ммоль/л)	D (ммоль/л ²)	Мо (ммоль/л)	Ме (ммоль/л)	Q₂₅ (ммоль/л)	Q₇₅ (ммоль/л)
4,45	72	4,2	4,0	3,3	6,0

По этим данным видно, что среднее значение, мода и медиана входят в пределы нормы. Однако, нижний квартиль Q₂₅ соответствует нижней границе нормы, т.е. 25% обследованных лиц имеют показатель меньше 3,3 ммоль/л - пониженное содержание сахара в крови. Аналогично верхний квартиль Q₇₅ показывает, что 25% совокупности имеют повышенные показатели, более 6,0 ммоль/л. Таким образом, половина обследованных нуждаются в пристальном внимании врачей.

Пример. На графике приведены изменения пульса у группы лиц после пробежки на короткую дистанцию. В среднем пульс остался на прежнем уровне - 73-74 уд/мин. Но значительно изменились размах и дисперсия. Это свидетельствует о том, что реакции на нагрузку были разнообразными, не просто увеличилась разница между минимальным и максимальным пульсом (размах), а у каждого из испытуемых произошли изменения – у одних увеличение по отношению к среднему, у других – уменьшение ЧСС, как результат произошел рост дисперсии.

Пример. У врачей появилось подозрение, что подростки, перенесшие некое инфекционное заболевание, отстают в росте от своих сверстников. Для проверки этого было проведено исследование среди данного контингента детей. Результаты сведены в нижеприведенную таблицу 8.

Таблица 8. Статистические данные по росту подростков

Возраст (лет)	(см)	М_о (см)	М_е (см)	нормативы
10-12	138,5			133-142 см

Средний рост 138,5 см укладывается в нормативы роста для этой возрастной группы. Наиболее часто встречающееся значение роста (мода=139 см) также в пределах нормы. Настораживает медиана – значение, находящееся в центре ранжированного ряда и делящее его пополам. Согласно ей половина мальчиков имеет рост меньше 128 см, т.е. отстают от своих сверстников.

Контрольное задание 3:

По данным из таблицы 9 найдите среднее значение, моду, медиану, нижний и верхний квартили, межквартильный размах.

Таблица 9. Таблица частот

Сон (час/сут)	Число случаев	Процент случаев