Квадратное уравнение
aх 2+ bх + c =0 (a, b, c Î R, a ¹ 0)
D = b 2-4 ac
· D >0 Þ $ x 1¹ x 2Î R (если дискриминант положителен, то квадратное уравнение имеет два различных действительных корня):
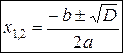· D =0 Þ $ x 1= x 2Î R (если дискриминант равен нулю, то квадратное уравнение имеет два совпавших действительных корня):
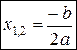· D <0 Þ  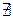R – корней(если дискриминант отрицателен, то квадратное уравнение не имеет действительных корней).
| Теорема Виета
· Пусть х 1, х 2 – корни неприведённого квадратного уравнения ах 2+ bх + c =0, тогда:
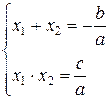· Пусть х 1, х 2 – корни приведённого квадратного уравнения х 2+ bх + c =0, тогда:
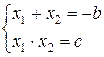– сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно третьему коэффициенту.
|
Задание 1. Решить уравнение (на множестве комплексных чисел) и проверить его корни подстановкой и по теореме Виета:
1)
| Проверка 1:
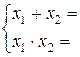Проверка 2:
| 2)
| Проверка 1: Проверка 2: |
3)
х 2+4 х +5=0
D =16-20=-4 D <0 Þ 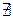R – корней, но существуют два сопряжённых комплексных корня
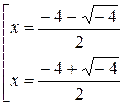
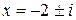
| Проверка 1: Проверка 2: | 4) х 2-4 х +5=0 | Проверка 1: Проверка 2: |
| 5) х 2-6 х +10=0 | Проверка 1: Проверка 2: | 6) х 2+6 х +10=0 | Проверка 1: Проверка 2: |
Задание 2. Произвести действия над комплексными числами в алгебраической форме:
z 1=2-5 i; z 2=-3+ i
1) z 1+ z 2= z 2+ z 1=(2-5 i)+(-3+ i)=
– коммутативность сложения;
2) z 1- z 2=-(z 2- z 1)=(2-5 i)-(-3+ i)=
– антикоммутативность вычитания или коммутативность сложения;
3) z 1· z 2= z 2· z 1=(2-5 i)·(-3+ i)=
– коммутативность умножения;
4) 
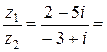5) 
или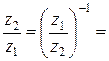 
| z 1=-4+2 i; z 2=1-3 i
1) z 1+ z 2= z 2+ z 1=
– коммутативность сложения;
2) z 1- z 2=-(z 2- z 1)=
– антикоммутативность вычитания или коммутативность сложения;
3) z 1· z 2= z 2· z 1=
– коммутативность умножения;
4) 
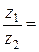5) 
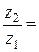или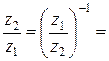
|
Задание 3.
1. произвести действия над комплексными числами в алгебраической форме;
2. представить комплексные числа в тригонометрической форме;
3. произвести действия над комплексными числами в тригонометрической форме;
4. сравнить полученные результаты:
z 1=-2+2 i; z 2=1- i
| 1) z 1+ z 2= z 2+ z 1=
2) z 1- z 2=
3) z 2- z 1=
4) z 1· z 2= z 2· z 1=
5)
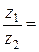6)
| |
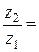
| Переведём комплексное число z 1 из алгебраической формы в тригонометрическую:
z 1=-2+2 i; а 1=; b 1=;
Вычислим модуль r 1 комплексного числа z 1:
Вычислим аргумент[1] j 1 комплексного числа z 1(в данном случае не будем вычислять, а воспользуемся знаниями из тригонометрии – так как «угол поворота – имеет точное значение»:
|
| z 1=-2+2 i = | |
|
| Переведём комплексное число z 1 из алгебраической формы в тригонометрическую:
z 2=1- i; а 2=; b 2=;
Вычислим модуль r 2 комплексного числа z 2:
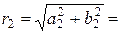Вычислим аргумент j 2 комплексного числа z 2(в данном случае не будем вычислять, а воспользуемся знаниями из тригонометрии – так как «угол поворота – имеет точное значение»:
|
| z 2=1- i = | |
| 1) z 1+ z 2= z 2+ z 1=
2) z 1- z 2=
3) z 2- z 1=
4) z 1· z 2= z 2· z 1=
5)
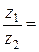6)
|
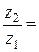
z 1=-2-2 i; z 2=4-4 i
| 1) z 1+ z 2= z 2+ z 1=
2) z 1- z 2=
3) z 2- z 1=
4) z 1· z 2= z 2· z 1=
5)
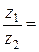6)
| |
|
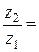
| Переведём комплексное число z 1 из алгебраической формы в тригонометрическую:
z 1=-2-2 i; а 1=; b 1=;
Вычислим модуль r 1 комплексного числа z 1:
Вычислим аргумент j 1 комплексного числа z 1(в данном случае не будем вычислять, а воспользуемся знаниями из тригонометрии – так как «угол поворота – имеет точное значение»:
|
| z 1=-2-2 i = | |
|
| Переведём комплексное число z 1 из алгебраической формы в тригонометрическую:
z 2=4-4 i; а 2=; b 2=;
Вычислим модуль r 2 комплексного числа z 2:
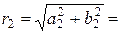Вычислим аргумент j 2 комплексного числа z 2(в данном случае не будем вычислять, а воспользуемся знаниями из тригонометрии – так как «угол поворота – имеет точное значение»:
|
| z 2=4-4 i = | |
| 1) z 1+ z 2= z 2+ z 1=
2) z 1- z 2=
3) z 2- z 1=
4) z 1· z 2= z 2· z 1=
5)
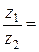6)
|
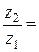
Домашнее задание
