1 – 25. Решить систему трех линейных уравнений с тремя неизвестными методом Крамера.
1. 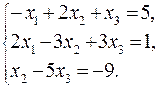 2.
2. 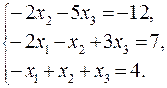
3.  4.
4. 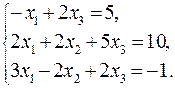
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 
13.  14.
14. 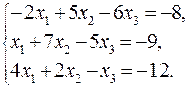
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 
21.  22.
22. 
23.  24.
24. 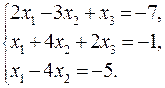
25. 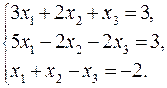
26 - 50. Даны координаты вершин пирамиды  .
.
Найти:
1) длину ребра  ;
;
2) угол между ребрами  и
и  ;
;
3) площадь грани  ;
;
4) объем пирамиды;
5) уравнение прямой  .
.
26. А1 (-1; 2; 1), А2 (-2; 2; 5), А3 (-3; 3; 1), А4 (-1; 4; 3).
27. А1 (7; 7; 3), А2 (6; 5; 8), А3 (3; 5; 8), А4 (8; 4; 1).
28. А1 (4; 2; 5), А2 (0; 7; 2), А3 (0; 2; 7), А4 (1; 5; 0).
29. А1 (4; 4; 10), А2 (-4; 10; 2), А3 (2; 8; 4), А4 (9; 6; 9).
30. А1 (-2; 1; -1), А2 (-3; 1; 3), А3 (-4; 2; -1), А4 (-2; 3; 1).
31. А1 (1; 1; 2), А2 (0; 1; 6), А3 (-1; 2; 2), А4 (1; 3; 4).
32. А1 (-1; -2; 1), А2 (-2; -2; 5), А3 (-3; -1; 1), А4 (-1; 0; 3).
33. А1 (2; -1; 1), А2 (1; -1; 5), А3 (0; 0; 1), А4 (2; 1; 3).
34. А1 (-1; 1; -2), А2 (-2; 1; 2), А3 (-3; 2; -2), А4 (-1; 3; 0).
35. А1 (4; 6; 5), А2 (6; 9; 4), А3 (2; 10; 10), А4 (7; 5; 9).
36. А1 (3; 5; 4), А2 (8; 7; 4), А3 (5; 10; 4), А4 (4; 7; 8).
37. А1 (10; 6; 6), А2 (-2; 8; 2), А3 (6; 8; 9), А4 (7; 10; 3).
38. А1 (1; 8; 2), А2 (5; 2; 6), А3 (5; 7; 4), А4 (4; 10; 9).
39. А1 (6; 6; 5), А2 (4; 9; 5), А3 (4; 6; 11), А4 (6; 9; 3).
40. А1 (7; 2; 2), А2 (5; 7; 7), А3 (5; 3; 1), А4 (2; 3; 7).
41. А1 (8; 6; 4), А2 (10; 5; 5), А3 (5; 6; 8), А4 (8; 10; 7).
42. А1 (1; 2; 1), А2 (0; 2; 5), А3 (-1; 3; 1), А4 (1; 4; 3).
43. А1 (-2; -1; 1), А2 (-3; -1; 5), А3 (-4; 0; 1), А4 (-2; 1; 3).
44. А1 (1; -1; 2), А2 (0; -1; 6), А3 (-1; 0; 2), А4 (1; 1; 4).
45. А1 (1; -2; 1), А2 (0; -2; 5), А3 (-1; -1; 1), А4 (1; 0; 3).
46. А1 (0; 3; 2), А2 (-1; 3; 6), А3 (-2; 4; 2), А4 (0; 5; 4).
47. А1 (-1; 2; 0), А2 (-2; 2; 4), А3 (-3; 3; 0), А4 (-1; 4; 2).
48. А1 (2; 2; 3), А2 (1; 2; 7), А3 (0; 3; 3), А4 (2; 4; 5).
49. А1 (0; -1; 2), А2 (-1; -1; 6), А3 (-2; 0; 2), А4 (0; 1; 4).
50. А1 (3; 0; 2), А2 (2; 0; 6), А3 (1; 1; 2), А4 (3; 2; 4).
51 – 75. Вычислить пределы функций а), б), г), не пользуясь правилом Лопиталя. Предел функции в) вычислить по правилу Лопиталя.
51. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 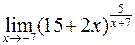 .
.
52. а) 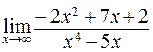 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
53. а)  ; б)
; б) 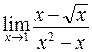 ;
;
в)  ; г)
; г)  .
.
54. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
55. а)  ; б)
; б) 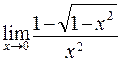 ;
;
в)  ; г)
; г) 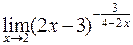 .
.
56. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
57. а)  ; б)
; б) 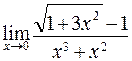 ;
;
в) 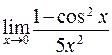 ; г)
; г)  .
.
58. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 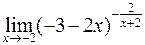 .
.
59. а) 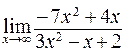 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
60. а) 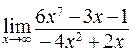 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
61. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
62. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
63. а) 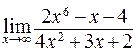 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
64. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
65. а)  ; б
; б 
в) 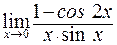 ; г)
; г)  .
.
66. а)  ; б)
; б) 
в) 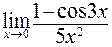 ; г)
; г)  .
.
67. а) 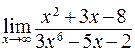 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
68. а) 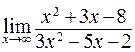 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
69. а)  б)
б)  ;
; 
в)  ; г)
; г)  .
.
70. а)  ; б)
; б)  ;
; 
в)  ; г)
; г)  .
.
71. а)  ; б)
; б) 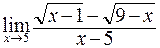 ;
;
в)  ; г)
; г)  .
.
72. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 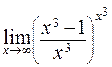 .
.
73. а)  ; б)
; б) 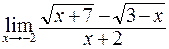 ;
;
в)  ; г)
; г)  ;
;
74. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 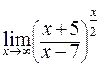 .
.
75. а)
 ; б)
; б)  ;
; 
в)  ; г)
; г)  .
.
76 – 100. Найти производную функции:
76.  . 77.
. 77.  .
.
78.  . 79.
. 79.  .
.
80.  . 81.
. 81.  .
.
82.  . 83.
. 83.  .
.
84.  . 85.
. 85.  .
.
86.  . 87.
. 87.  .
.
88.  . 89.
. 89. 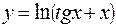 .
.
90.  . 91.
. 91.  .
.
92.  . 93.
. 93.  .
.
94.  . 95.
. 95.  .
.
96.  . 97.
. 97.  .
.
98.  . 99.
. 99. 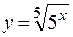 .
.
100.  .
.
101 – 125. Исследовать функцию средствами дифференциального исчисления и, используя результаты исследования, построить график.
101.  . 102.
. 102.  .
.
103.  . 104.
. 104.  .
.
105.  . 106.
. 106.  .
.
107.  . 108.
. 108.  .
.
109.  . 110
. 110  .
.
111.  . 112.
. 112.  .
.
113.  . 114.
. 114.  .
.
115.  . 116.
. 116.  .
.
117. 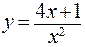 . 118.
. 118.  .
.
119.  . 120.
. 120.  .
.
121.  . 122.
. 122.  .
.
123.  . 124.
. 124. 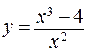 .
.
125.  .
.
Решите задачи
126. Имеются 5 карточек разрезной азбуки с буквами Р, О, П, А, Ж. Какова вероятность того, что выбранные наугад три карточки образуют слово «жар»?
127. В партии из 30 деталей – 4 дефектных. Определите вероятность того, что среди 5 выбранных деталей ровно две детали окажутся дефектными.
128. Имеются 5 карточек с цифрами 1, 2, 3, 4, 5. Найти вероятность того, что на разложенных в произвольном порядке карточках получится число 24315.
129. Набирая номер телефона, абонент забыл последние две цифры и, помня, что они различны, набрал их наугад. Найти вероятность того, что набраны нужные цифры.
130. В партии из 10 деталей семь деталей стандартных. Найти вероятность того, что среди взятых наугад пяти деталей три детали стандартные.
131. Восемь различных книг расставляются наудачу на одной полке. Найти вероятность того, что две определенные книги окажутся поставленными рядом.
132. Из карточек оставлено слово ПОБЕДА. Буквы перемешаны. Найти вероятность того, что две наугад выбранные буквы – гласные.
133. Набирая номер телефона, абонент забыл последние 3 цифры и набрал их наудачу, помня, что они различны. Найти вероятность того, что набраны нужные цифры.
134. В ящике 15 деталей, среди которых 10 деталей являются стандартными. Сборщик наудачу выбрал 3 детали. Найти вероятность того, что все детали будут стандартными.
135. Из колоды карт (52 штуки) наугад выбирают 3 карты. Какова вероятность того, что это будут тройка, семерка, туз?
136. В группе 30 студентов, среди которых 8 отличников. Случайным образом отбирают 12 студентов. Найти вероятность того, что отберут 5 отличников.
137. В ящике 6 белых и 4 черных шарика. Из ящика наугад вынимается 3 шарика. Чему равна вероятность того, что все шарики окажутся белыми?
138. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5.
139. Круговая мишень состоит из зон с номерами 1, 2, 3. Вероятности попадания в эти зоны при одном выстреле соответственно равны 0,1; 0,35 и 0,4. Найти вероятность попадания в первую или третью зону.
140. Пусть А и В – некоторые события, связанные с одним опытом, причем Р(А) = 0,25 и Р(В) = 0,35. Предполагая, что А и В независимы, вычислите вероятность того, что произошло одно из событий А и В.
141. Студент разыскивает нужную ему формулу в трех справочниках. Вероятность того, что формула содержится в 1, 2 и 3 справочнике соответственно равна 0,6; 0,7; 0,8. Найти вероятность того, что формула содержится только в двух справочниках.
142. Брошены 3 игральные кости. Определить вероятность того, что выпадет три «шестерки».
143. В группе 25 студентов, из них 10 юношей и 15 девушек. Какова вероятность того, что из вызванных наудачу трех студентов первые две девушки, третий – юноша?
144. Ученик получает оценку от 2 до 5 баллов. Вероятности того, что ему поставят «4», «3» и «2», соответственно равны 0,45, 0,23 и 0,09. Определите вероятность того, что он получит оценку не ниже «4».
145. В группе, состоящей из 25 студентов, спортивный разряд по борьбе имеют 10 человек, по стрельбе – 12. Вероятность того, что студент этой группы имеет разряды по обоим видам спорта, равна 0,32. Найдите вероятность того, что наугад выбранный студент имеет какой-нибудь разряд.
146. Из 40 деталей в ящике 5 бракованных. Наудачу одну за другой берут две детали, не возвращая их обратно. Какова вероятность того, что первой возьмут стандартную деталь, а второй нестандартную?
147. В коробке 10 черных и 14 красных шаров. Найти вероятность того, что первым возьмут черный шар, а вторым красный.
148. Два стрелка произвели по одному выстрелу. Вероятность попадания в мишень первым стрелком равна 0,5, вторым 0,7. Найти вероятность того, что хотя бы один из стрелков попадет в мишень.
149. Имеются два ящика, содержащих по 10 деталей. В первом ящике 8, во втором 7 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найдите вероятность того, что обе взятые детали окажутся стандартными.
150. В ящике 40 апельсинов: 20 - первого сорта, 15 - второго сорта, 5 - третьего сорта. Найти вероятность того, что наугад извлеченный апельсин окажется не третьего сорта.
151 – 175. Вычислить:
а) неопределенный интеграл;
б) неопределенный интеграл;
в) определенный интеграл.
151. а)  б)
б)  ;
;
в)  .
.
152. а)  ; б)
; б)  ;
;
в)  .
.
153. а)  ; б)
; б)  ;
;
в)  .
.
154. а) 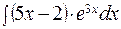 ;
;
б)  ;
;
в) 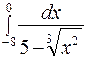 .
.
155. а)  ; б)
; б)  ;
;
в)  .
.
156. а) 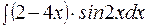 ; б)
; б)  ;
;
в)  .
.
157. а)  ; б)
; б)  ;
;
в)  .
.
158. а)  ; б)
; б) 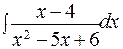 ;
;
в);  .
.
159. а)  ; б)
; б)  ;
;
в)  .
.
160. а)  ; б)
; б)  ;
;
в)  .
.
161. а)  ; б)
; б)  ;
;
в)  .
.
162. а)  ; б)
; б)  ;
;
в)  .
.
163. а)  ; б)
; б)  ;
;
в) 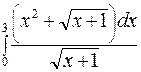 .
.
164. а) 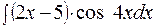 ; б)
; б)  ;
;
в)  .
.
165. а)  ; б)
; б) 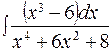 ;
;
в)  .
.
166. а)  ; б)
; б)  ;
;
в)  .
.
167. а) 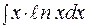 ; б)
; б)  ;
;
в)  .
.
168. а)  ; б)
; б)  ;
;
в)  .
.
169. а)  ; б)
; б)  ;
;
в)  .
.
170. а)  ; б)
; б)  ;
;
в)  .
.
171. а)  ; б)
; б)  ;
;
в)  .
.
172. а)  ; б)
; б)  ;
;
в)  .
.
173. а)  ; б)
; б)  ;
;
в) 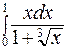 .
.
174. а) 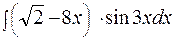 ; б)
; б)  ;
;
в)  .
.
175. а)  ; б)
; б)  ;
;
в)  .
.
176 – 188. Решить задачу с использованием формулы Бернулли.
176. Найти вероятность того, что при четырех подбрасываниях игральной кости 5 очков появится два раза.
177. Вероятность выбора отличника на факультете равна 1/7. Из 28 студентов группы наудачу вызываются три студента. Определить вероятности всех возможных значений числа отличников, которые могут оказаться среди вызванных трех студентов.
178. Вероятность того, что родится мальчик, равна 0,51. Какова вероятность того, что в семье, имеющей 6 детей, больше девочек, чем мальчиков?
179. В телевизоре 10 ламп. Для любой из ламп вероятность, что она останется исправной в течение года, равна 0,9. Какова вероятность того, что в течение года ровно одна лампа выйдет из строя?
180. Какова вероятность того, что из 5 подбрасываний монеты герб выпадет более двух раз?
181. Вероятность победы спортсмена в матче равна 0,6. Какова вероятность того, что в 10 поединках он одержит более 8 побед?
182. В семье 5 детей. Считая вероятности рождений мальчика и девочки одинаковыми, найти вероятность того, что среди этих детей не более двух мальчиков.
183. Игральная кость подбрасывается 7 раз. Определить вероятность того, что грань с «единицей» выпадет не менее 5 раз.
184. Из набора домино 5 раз случайно выбирается кость и возвращается обратно. Найдите вероятность того, что 3 раза будет вынута кость, являющаяся дублем.
185. В семье 5 детей. Считая вероятности рождений мальчика и девочки одинаковыми, найти вероятность того, что среди этих детей не менее двух и не более трех мальчиков.
186. Найти вероятность того, что при четырех подбрасываниях игральной кости 5 очков появится хотя бы один раз.
187. В телевизоре 10 ламп. Для любой из ламп вероятность, что она останется исправной в течение года, равна 0,99. Какова вероятность того, что в течение года хотя бы одна лампа выйдет из строя?
188. В квартире 4 лампочки. Для каждой лампочки вероятность того, что она останется исправной в течение года, равна 5/6. Какова вероятность того, что в течение года придется заменить не меньше половины лампочек?
189 - 200. Решить задачу с использованием формулы полной вероятности или формулы Байеса.
189. В ящике содержится 20 деталей с завода № 1, 15 деталей с завода № 2, 15 деталей с завода № 3. Вероятность того, что деталь с завода № 1 отличного качества, равна 0,6. Вероятность того, что деталь с завода № 2 отличного качества, равна 0,9. Вероятность того, что деталь с завода № 3 отличного качества, равна 0,8. Найти вероятность того, что наудачу извлеченная деталь отличного качества.
190. На складе имеются 60 телефонных аппаратов, из них 15 изготовлены на 1-ом заводе, 20 изготовлены на 2-ом заводе, 25 изготовлены на 3-ем заводе. Вероятность выпуска аппаратов высшего сорта на 1-ом заводе равна 2/3, на 2-ом заводе равна 3/4, на 3-ем заводе равна 4/5. Найти вероятность того, что взятый наудачу аппарат окажется высшего сорта.
191. В двух корзинах имеются шары. В 1-ой корзине 14 шаров, из них 3 зеленого цвета. Во 2-ой корзине 10 шаров, из них 2 зеленого цвета. Из второй корзины взят один шар (наудачу) и переложен в первую корзину. Найти вероятность того, что взятый наугад шар из первой корзины окажется зеленым.
192. Сборщик получил 5 коробок с завода № 1 и 3 коробки с завода № 2. Вероятность того, что деталь завода № 1 стандартная, равна 0,8, а завода № 2 равна 0,9. Сборщик наудачу извлек деталь из наугад взятой коробки. Найти вероятность того, что извлечена стандартная деталь.
193. В первой урне находятся 2 белых шара и 3 черных, во второй 6 белых и 4 черных, в третьей – поровну белых и черных. Наудачу выбирается урна, и из нее вынимается шар. Найдите вероятность того, что он будет белым.
194. В пирамиде 19 винтовок, из них 3 с оптическим прицелом. Стрелок, стреляя из винтовки с оптическим прицелом, может поразить мишень с вероятностью 0,81, без оптического прицела – с вероятностью 0,46. Найти вероятность того, что стрелок поразит мишень, стреляя из винтовки, взятой наугад из пирамиды.
195. Покупатель с равной вероятностью посещает 3 магазина. Вероятность того, что он купит товар в первом магазине, равна 0,4, во втором - 0,3, в третьем - 0,2. Определить вероятность того, что покупатель купит товар только в одном магазине.
196. В первой бригаде производится в три раза больше продукции, чем во второй. Вероятность того, что производимая продукция окажется стандартной для первой бригады, равна 0,7, для второй – 0,8. Взятая наугад единица продукции оказалась стандартной. Какова вероятность того, что она из второй бригады?
197. Имеется 5 урн. В первой, второй и третьей находится по 4 белых и 6 черных шаров, в четвертой и пятой урнах - по 2 белых и 3 черных шара. Случайно выбирается урна и из нее извлекается шар. Какова вероятность того, что была выбрана четвертая, если извлеченный шар оказался белым?
198. 1/3 ламп производится на первом заводе, 1/4 – на втором, остальные – на третьем. Вероятности брака в продукции первого, второго и третьего заводов соответственно равны 0,2, 0,15 и 0,05. Найдите вероятность того, что бракованная лампа произведена на первом заводе.
199. Каждое изделие проверяется одним из двух контролеров. Первый обнаруживает дефекты с вероятностью 0,85, второй – с вероятностью 0,7. Имевшийся в изделии дефект не был обнаружен. Какова вероятность того, что его проверял второй контролер?
200. В коробке находятся 4 новых и 2 уже использованных теннисных мяча. Для первой игры берут из коробки 2 мяча, а затем их возвращают после игры в коробку. Найти вероятность того, что для второй игры будут вытянуты два новых мяча.
Основные формулы
1. | 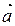 | =
| = 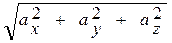 - модуль вектора
- модуль вектора
2. Формулы деления отрезка в данном отношении:
 ,
,  , где
, где  - отношение
- отношение  .
.
3. Линейные операции над векторами в координатной форме:
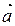 = (ax, ау, аz) и
= (ax, ау, аz) и  = (bx; bу; bz)
= (bx; bу; bz)
· 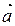

 = (ax
= (ax  bx; ау
bx; ау  bу; аz
bу; аz  bz).
bz).
· 
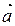 = (
= ( ax;
ax;  ау ;
ау ;  аz).
аz).
· 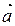 =
= 

· коллинеарность векторов:  =
=  .
.
4. Формула скалярного произведения 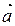
 = |
= |  | * |
| * |  | cos (
| cos ( ,
,  ), где φ = (
), где φ = (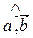 ).
).
5. Скалярное произведение в координатной форме 
 = axbx + ауbу + аzbz.
= axbx + ауbу + аzbz.
6. Формула для нахождения угла между векторами cos ( ,
,  ) =
) =  .
.
7. Векторное произведение в координатной форме
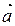

 =
=  .
.
8. 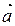 ||
|| 

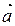

 =
=  (и наоборот), т.е.
(и наоборот), т.е. 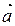

 =
=  =
= 

 =
=  =
=  .
.
9. Sпар. = | 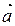

 |, Sтр. =
|, Sтр. = 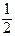 |
| 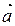

 |.
|.
10. Смешанное произведение векторов в координатной форме
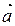

 =
=  .
.
11. 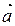

 = 0
= 0 
 = 0
= 0  векторы
векторы 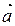 ,
,  ,
,  компланарны.
компланарны.
12. Объем параллелепипеда: V = | 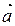

 |.
|.
Объем треугольной пирамиды: V =  |
| 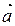

 |.
|.
13. Ах + By + С = 0 - общее уравнение прямой, где А, В, С – произвольные числа.
14. Уравнение прямой, проходящей через данную точку мо (хо; уо)с направляющим вектором (с; d)
 .
.
1. Уравнение прямой, проходящей через две точки
М1 (x1; y1)и М2 (x2; y2):
 .
.
16. А (х - х0) + В (у – у0) = 0 - уравнение прямой, проходящей через заданную точку перпендикулярно заданному вектору, где (А; В)координаты нормального вектора прямой, (х0; у0) координаты текущей точки,а х и у переменные.
17. Формула для нахождения расстояния от точки (х 1; у 1) до прямой Ах + By + С = 0:  .
.
18. (х + х 0)2 + (у + у 0)2 = r 2– каноническое уравнение окружности с центром в точке (х 0; у 0), радиусом r.
19.  - каноническое уравнение эллипса.
- каноническое уравнение эллипса.
20.  - каноническое уравнение гиперболы.
- каноническое уравнение гиперболы.
21. Канонические уравнения парабол: у2 = 2рх, у2 = —2рх, х2 = 2ру,
х2 = —2ру (р > 0).
22. Основные теоремы о пределах:
· Если  f(х) = А, то он единственный.
f(х) = А, то он единственный.
·  (f(х) ± g(x)) =
(f(х) ± g(x)) =  f(х) ±
f(х) ±  g(x) = А ± В
g(x) = А ± В
·  (f(х) * g(x)) =
(f(х) * g(x)) =  f(х) *
f(х) *  g(x) = А * В
g(x) = А * В
·  С f(х) = С
С f(х) = С  f(х)
f(х)
·  (f(х)) n = (
(f(х)) n = ( f(х)) n = Аn
f(х)) n = Аn
· 
 =
=  =
=  (
( g(x)
g(x)  0)
0)
23. Первый замечательный предел:
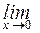
 = 1;
= 1; 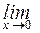
 = 1;
= 1; 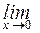
 = 1.
= 1.
24. Второй замечательный предел:
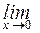 (1 + х)
(1 + х)  = е;
= е;  (1 +
(1 +  )х = е.
)х = е.
25. Производная функции  в точке
в точке  :
: 
26.  - уравнение касательной.
- уравнение касательной.
27.  - уравнение нормали.
- уравнение нормали.
28. 
29. 
30. 
31. Производная сложной функции:  .
.
32. Производная функции, заданная параметрически:
 х =
х =  ,
,  х х =
х х =  .
.
33. Формулы дифференцирования
| № п/п | Производная простой функции | Производная сложной функции |

| ||

| ||

| 
| |

| 
| |

| 
| |

| 
| |

| 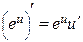
| |

| 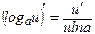
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 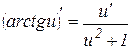
| |

| 
|
34. Формула дифференциала функции:  .
.
35.  .
.
36. 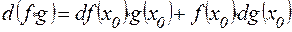 .
.
37.  .
.
38.
·  ,
,
·  ,
,
· 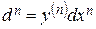 .
.






