ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ СВЕРДЛОВСКОЙ ОБЛАСТИ
«УРАЛЬСКИЙ КОЛЛЕДЖ СТРОИТЕЛЬСТВА, АРХИТЕКТУРЫ И ПРЕДПРИНИМАТЕЛЬСТВА»
Математика
(базовый уровень)
Методические указания и варианты контрольной работы
для студетов факультета заочного обучения
2016 г.
Выполнение и оформление контрольных работ
Слушатели выполняют контрольную работу в соответствии с учебным рабочим планом в сроки, установленные факультетом заочного обучения.
Слушатели должны выполнить один из 100 вариантов, номер которого определяется по двум последним цифрам номера зачетной книжки.
Контрольная работа выполняется в отдельной тетради в клеточку ручкой любого цвета, кроме зеленого и красного, аккуратно и разборчивым почерком, чертежи выполняются простым карандашом с использованием инструмента.
На титульном листе следует указать фамилию, имя, отчество, номер зачетной книжки, номер варианта.
Задания в контрольных работах выполняются по порядку, согласно расположению их в варианте.
Варианты контрольной работы
| № варианта | Задания | № варианта | Задания |
| 1, 50, 74, 98, 122, 146, 170, 176 | |||
| 2, 26, 75, 99, 123, 147, 171, 177 | 3, 27, 51, 100, 124, 148, 172, 178 | ||
| 4, 28, 52, 76, 125, 149, 173, 179 | 5, 29, 53, 77, 101, 150, 174, 180 | ||
| 6, 30, 54, 78, 102, 126, 175, 181 | 7, 31, 55, 79, 103, 127, 151, 182 | ||
| 8, 32, 56, 80, 104, 128, 152, 183 | 9, 33, 57, 81, 105, 129, 153, 184 | ||
| 10, 34, 58, 82, 106, 130, 154, 185 | 11, 35, 59, 83, 107, 131, 155, 186 | ||
| 12, 36, 60, 84, 108, 132, 156, 187 | 13, 37, 61, 85, 109, 133, 157, 188 | ||
| 14, 38, 62, 86, 110, 134, 158, 189 | 15, 39, 63, 87, 111, 135, 159, 190 | ||
| 16, 40, 64, 88, 112, 136, 160, 191 | 17, 41, 65, 89, 113, 137, 161,192 | ||
| 18, 42, 66, 90, 114, 138, 162, 193 | 19, 43, 67, 91, 115, 139, 163, 194 | ||
| 20, 44, 68, 92, 116, 140, 164, 195 | 21, 45, 69, 93, 117, 141, 165, 196 | ||
| 22, 46, 70, 94, 118, 142, 166, 197 | 23, 47, 71, 95, 119, 143, 167, 198 | ||
| 24, 48, 72, 96, 120, 144, 168, 199 | 25, 49, 73, 97, 121, 145, 169, 200 | ||
| 1, 48, 51, 99, 101, 149, 151, 176 | 2, 48, 52, 98, 102, 148, 152, 177 | ||
| 3, 47, 53, 97, 103, 147, 153, 178 | 4, 46, 54, 96, 104, 146, 154, 179 | ||
| 5, 45, 55, 95, 105, 145, 155, 180 | 6, 44, 56, 94, 106, 144, 156, 181 | ||
| 7, 43, 57, 93, 107, 143, 157, 182 | 8, 42, 58, 92, 108, 142, 158, 183 | ||
| 9, 41, 59, 91, 109, 141, 159, 184 | 10, 40, 60, 90, 110, 140, 160, 185 | ||
| 11, 39, 61, 89, 111, 139, 161, 186 | 12, 38, 62, 88, 112, 138, 162, 187 | ||
| 13, 37, 63, 87, 113, 137, 163, 188 | 14, 36, 64, 86, 114, 136, 164, 189 | ||
| 15, 35, 65, 85, 115, 135, 165, 190 | 16, 34, 67, 84, 116, 134, 166, 191 | ||
| 17, 33, 67, 83, 117, 133, 167, 192 | 18, 32, 68, 82, 118, 132, 168, 193 | ||
| 19, 31, 69, 81, 119, 131,169, 194 | 20, 30, 70, 80, 120, 130, 170, 195 | ||
| 21, 29, 71, 79, 121, 129, 171, 196 | 22, 28, 72, 78, 122, 128, 172, 197 | ||
| 23, 27, 73, 77, 123, 127, 173, 198 | 24, 26, 74, 76, 124, 126, 174, 199 | ||
| 25, 50, 75, 100, 125, 150,175, 200 | 1, 50, 51, 100, 101, 150, 151, 176 | ||
| 2, 49, 52, 99, 102, 149, 152, 177 | 3, 48, 53, 98, 103, 148, 153, 178 | ||
| 4, 47, 54, 97, 104, 147, 154, 179 | 5, 46, 55, 96, 105, 146, 155, 180 | ||
| 6, 45, 56, 95, 106, 145, 156, 181 | 7, 44, 57, 94, 107, 144, 157, 182 | ||
| 8, 43, 58, 93, 108, 143, 158, 183 | 9, 42, 59, 92, 109, 142, 159, 184 | ||
| 10, 41, 60, 91, 110, 141, 160, 185 | 11, 40, 61, 90, 111, 140, 161, 186 | ||
| 12, 39, 62, 89, 112, 139, 162, 187 | 13, 38, 63, 88, 113, 138, 163, 188 | ||
| 14, 37, 64, 87, 114, 137, 164, 189 | 15, 36, 65, 86, 115, 136, 165, 190 | ||
| 16, 35, 66, 85, 116, 135, 166, 191 | 17, 34, 67, 84, 117, 134, 167, 192 | ||
| 18, 33, 68, 83, 118, 133, 168, 193 | 19, 32, 69, 82, 119, 132, 169, 194 | ||
| 20, 31, 70, 81, 120, 131, 170, 195 | 21, 30, 71, 80, 121, 130, 171, 196 | ||
| 22, 29, 72, 79, 122, 129, 172, 197 | 23, 28, 73, 78, 123, 128, 173, 198 | ||
| 24, 27, 74, 77, 124, 127, 174, 199 | 25, 26, 75, 76, 125, 126, 175, 200 | ||
| 1, 49, 72, 95, 118, 141, 164, 176 | 2, 50, 73, 96, 119, 142, 165, 177 | ||
| 3, 26, 74, 97, 120, 143, 166, 178 | 4, 27, 75, 98, 121, 144, 167, 179 | ||
| 5, 28, 51, 99, 122, 145, 168, 180 | 6, 29, 52, 100, 123, 146, 169, 181 | ||
| 7, 30, 53, 76, 124, 147, 170, 182 | 8, 31, 54, 77, 125, 148, 171, 183 | ||
| 9, 32, 52, 78, 101, 149, 172, 184 | 10, 33, 56, 79, 102, 150, 173, 185 | ||
| 11, 34, 57, 80, 103, 126, 174, 186 | 12, 35, 58, 81, 104, 127, 175, 187 | ||
| 13, 36, 59, 82, 105, 128, 151, 188 | 14, 37, 60, 83, 106, 129, 152, 189 | ||
| 15, 38, 61, 84, 107, 130, 153, 190 | 16, 39, 62, 85, 108, 131, 154, 191 | ||
| 17, 40, 63, 86, 109, 132, 155, 192 | 18, 41, 64, 87, 110, 133, 156, 193 | ||
| 19, 42, 65, 88, 111, 134, 157, 194 | 20, 43, 66, 89, 112, 135, 158, 195 | ||
| 21, 44, 67, 90, 113, 136, 159, 196 | 22, 45, 68, 91, 114, 137, 160, 197 | ||
| 23, 46, 69, 92, 115, 138, 161, 198 | 24, 47, 70, 93, 116, 139, 162, 199 | ||
| 25, 48, 71, 94, 117, 140, 163, 200 |
Указания к выполнению контрольной работы
Примеры решения типовых задач
№ 1. Даны координаты вершин пирамиды А1 А2 А3 А4.:
А1 (0; 2; - 2), А2 (1; 0; - 1), А3 (0; 5; - 1), А4 (0; 2; 1).
Найти: 1) длину ребра А1 А2; 2) угол между ребрами А1 А2 и А1 А4; 3) площадь грани А1 А2 А3; 4) объем пирамиды; 5) уравнение прямой А1 А2.
Решение
1. Найти длину ребра А1 А2.
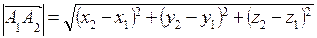
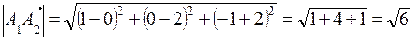 (ед)
(ед)
2. Найти угол между ребрами А1 А2 и А1 А4.
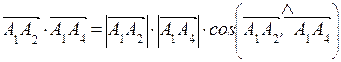 , отсюда
, отсюда
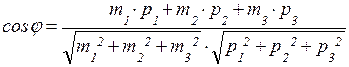 ,
,
где 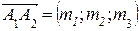 и
и 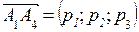 .
.
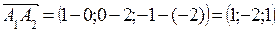 и
и 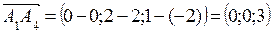 ,
,
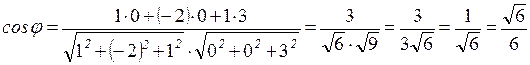 , значит,
, значит, 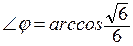 .
.
3. Найти площадь грани А1 А2 А3.
Найдем векторное произведение векторов 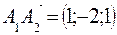 и
и 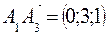 .
.
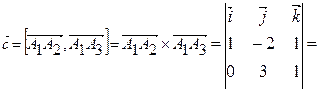
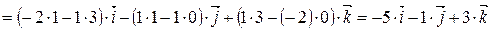
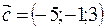
Площадь треугольника равна половине площади параллелограмма, т.е. Sтреугольника = 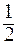
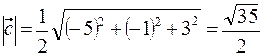 (ед2).
(ед2).
4. Найти объем пирамиды А1 А2 А3 А4.
Объем пирамиды равен одной шестой модуля смешанного произведения трех векторов, т.е.
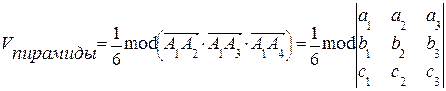 ,
,
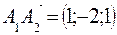 ,
, 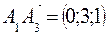 и
и  .
.
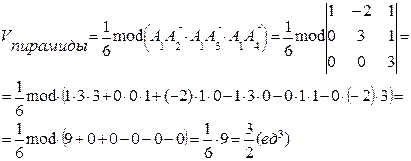
5. Составить уравнение прямой А1 А2.
 - направляющий вектор прямой
- направляющий вектор прямой  , точка
, точка  лежит на прямой. Тогда каноническое уравнение прямой
лежит на прямой. Тогда каноническое уравнение прямой 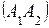 имеет вид:
имеет вид:  ,
,  .
.
№ 2. Вычислить:
1) Примеры и решение пределов с использованием теорем о пределах:
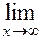 (1+
(1+ 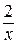 ) = 1 + 0 = 1;
) = 1 + 0 = 1;
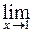 (4x3 - х + 2) =
(4x3 - х + 2) = 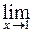 4x3 -
4x3 - 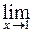 х +
х + 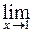 2 =4(
2 =4(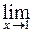 x)3 -
x)3 - 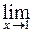 х +
х + 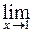 2= 4 * 1 - 1 + 2 = 5.
2= 4 * 1 - 1 + 2 = 5.
2) Примеры и решение пределов с использованием методов раскрытия неопределенностей, а также теорем о пределах:
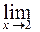
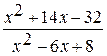 = [
= [ 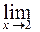
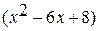 = 0,
= 0, 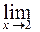 (
(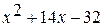 ) = 0] =
) = 0] =
= 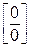 =
=
Для того чтобы раскрыть неопределенность вида 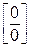 , надо под знаком предела числитель и знаменатель разложить на множители и сократить их далее на общий множитель.
, надо под знаком предела числитель и знаменатель разложить на множители и сократить их далее на общий множитель.
= 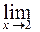
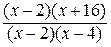 =
= 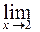
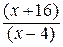 =
=  = - 9.
= - 9.
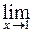
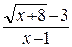 =
=
Здесь мы также имеем неопределенность вида 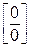 . Домножим числитель и знаменатель дроби на выражение, сопряженное числителю (избавляемся от иррациональности в числителе):
. Домножим числитель и знаменатель дроби на выражение, сопряженное числителю (избавляемся от иррациональности в числителе):
= 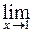
 =
= 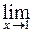
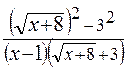 =
=
= 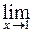
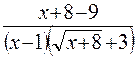 =
= 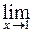
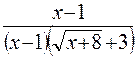 =
=
= 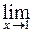
 = =
= = 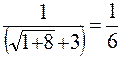 .
.
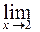
 =
=
Здесь мы также имеем неопределенность вида 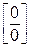 . Домножим числитель и знаменатель дроби на неполный квадрат суммы выражений
. Домножим числитель и знаменатель дроби на неполный квадрат суммы выражений 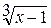 и 1, чтобы получить разность кубов в числителе:
и 1, чтобы получить разность кубов в числителе:
= 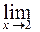
 =
= 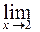
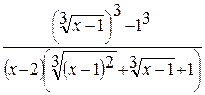 =
=
= 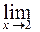
 =
= 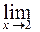
 =
=
= 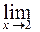
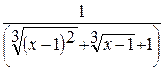 =
= 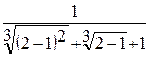 =
=  .
.
3) Вычислить:
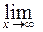
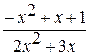 =
= 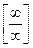 =
=
Для того чтобы раскрыть неопределенность вида 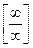 , надо под знаком предела числитель и знаменатель дроби разделить на переменную х с наивысшим показателем.
, надо под знаком предела числитель и знаменатель дроби разделить на переменную х с наивысшим показателем.
= 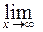
 =
= 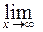
 =
=
Осталось воспользоваться теоремами о пределах, а также тем, что функции 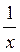 ,
,  и
и 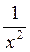 - бесконечно малые при х
- бесконечно малые при х 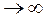 .
.
=  =
=  .
.
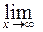
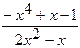 =
= 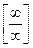 =
=
Для того чтобы раскрыть неопределенность вида 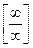 , надо под знаком предела числитель и знаменатель дроби разделить на переменную х с наивысшим показателем.
, надо под знаком предела числитель и знаменатель дроби разделить на переменную х с наивысшим показателем.
= 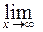
 =
= 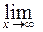
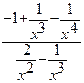 =
=
Осталось воспользоваться теоремами о пределах, а также тем, что функции 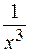 ,
,  и
и  - бесконечно малые при х
- бесконечно малые при х 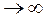 .
.
= 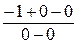 =
= 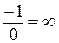 .
.
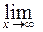
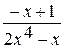 =
= 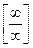 =
=
Для того чтобы раскрыть неопределенность вида 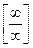 , надо под знаком предела числитель и знаменатель дроби разделить на переменную х с наивысшим показателем.
, надо под знаком предела числитель и знаменатель дроби разделить на переменную х с наивысшим показателем.
= 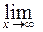
 =
= 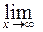
 =
=
Осталось воспользоваться теоремами о пределах, а также тем, что функции 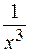 и
и  - бесконечно малые при х
- бесконечно малые при х 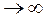 .
.
= 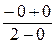 =
=  .
.
4) Примеры и решение пределов с помощью замечательных пределов:
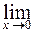
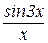 =
=
Домножим числитель и знаменатель дроби на «3» и получим:
= 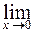
 =
=
Используя теоремы о пределах и первый замечательный предел, получаем:
= 3 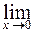
 =3.
=3.
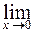
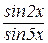 =
=
Поделим числитель и знаменатель дроби под знаком предела на х, после чего воспользуемся предыдущим примером, получим:
= 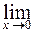
 =
= 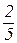 .
.
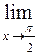
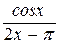 =
=
Сведем данный предел к первому замечательному пределу, для этого сделаем замену у = х - 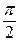 . Тогда
. Тогда 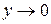 при х
при х 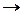
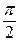 , а х = у +
, а х = у + 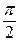 , откуда
, откуда
= 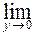
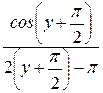 =
=
В числителе дроби используем формулу приведения, тогда
= 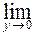
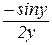 =
= 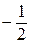
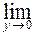
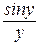 =
= 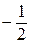 .
.
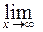 (1 +
(1 + 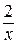 )
) 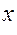 =
=
В данном случае неопределенность вида 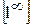 , для ее раскрытия сделаем замену у =
, для ее раскрытия сделаем замену у = 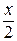 . Тогда
. Тогда  при
при 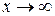 и исходный предел сводится ко второму замечательному пределу:
и исходный предел сводится ко второму замечательному пределу:
= 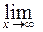
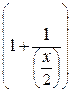
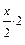 =
= 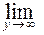
 =
= 
 =
= 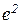 .
.
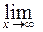
 =
=
Поделив числитель и знаменатель дроби на х, сведем данный предел ко второму замечательному пределу, т.е.
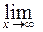
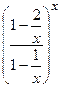 =
=  =
=
В числителе дроби сделаем замену у =  , а в знаменателе дроби t =
, а в знаменателе дроби t =  . Тогда
. Тогда  и
и  при
при 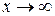 и исходный предел сводится ко второму замечательному пределу:
и исходный предел сводится ко второму замечательному пределу:
=  =
= 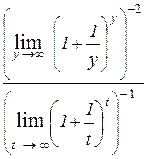 =
= 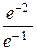 =
= 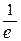 .
.
5) Вычислить предел по правилу Лопиталя.
 .
.
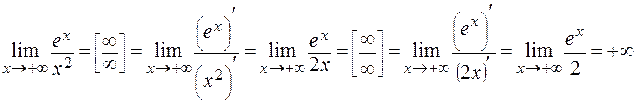 При вычислении производных используется таблица производных элементарных функций, применяются правила дифференцирования суммы, разности, произведения и частного функций, а также правило дифференцирования сложной функции.
При вычислении производных используется таблица производных элементарных функций, применяются правила дифференцирования суммы, разности, произведения и частного функций, а также правило дифференцирования сложной функции.
№ 4. Найти производную сложной функции:
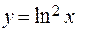
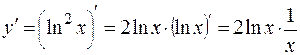 .
.
2) 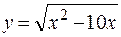
 .
.
3) 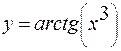
 .
.
№ 5.1) Исследовать функцию 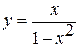 и построить ее график.
и построить ее график.
Решение
1. Функция терпит разрыв при х = 1 и х = - 1. При всех других значениях аргумента она непрерывна. Область ее определения состоит из трех интервалов 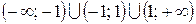 , а график из трех ветвей.
, а график из трех ветвей.
2. Функция является нечетной, так как у (-х) = -у (х), т.е.
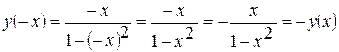 .
.
Следовательно, график ее симметричен относительно начала координат.
3. Найдем интервалы возрастания и убывания функции. Так как
 , то
, то
 > 0 в области определения, и функция является возрастающей на каждом интервале области определения.
> 0 в области определения, и функция является возрастающей на каждом интервале области определения.
4. Исследуем функцию на экстремум. Так как  , то критическими точками являются точки х = 1 и х = - 1 (
, то критическими точками являются точки х = 1 и х = - 1 ( не существует), но они не принадлежат области определения функции. Функция экстремумов не имеет.
не существует), но они не принадлежат области определения функции. Функция экстремумов не имеет.
5. Исследуем функцию на выпуклость. Найдем  :
:
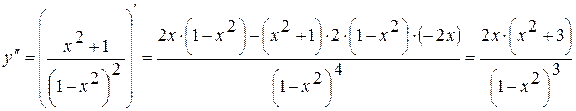 .
.
Вторая производная равна нулю или не существует в точках х =0, х=1 и х =-1.





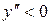

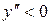
- 1 0 1 х
Точка О (0; 0) – точка перегиба графика функции.
График выпуклый вверх на интервале (-1; 0) и 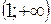 ; выпуклый вниз на интервалах
; выпуклый вниз на интервалах  и (0; 1).
и (0; 1).
6. Определим асимптоты графика функции. Прямые х=1 и х =-1 являются вертикальными асимптотами. Используя соответствующие формулы, выясним вопрос о наличии наклонной асимптоты:
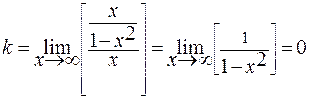
(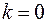 при
при 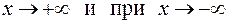 ),
),
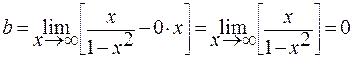 .
.
Следовательно, есть горизонтальная асимптота, ее уравнение у = 0.
7. Строим график:
 у
у
- 1 0 1 х
2) Исследовать функцию у = х 3 - 2 х 2 +2 х – 1 и построить ее график.
Решение
1. Область определения функции: D (f) = (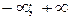 ). Функция непрерывна и определена при всех значениях х.
). Функция непрерывна и определена при всех значениях х.
2. Найдем (если это можно) точки пересечения графика с осями координат.
Точки пересечения с осью ординат находим, подставив значение х = 0 в функцию у = х 3 - 2 х 2 +2 х – 1:
у (0) = 03 -2·02 + 2∙0 – 1 = - 1, откуда получаем у = - 1.
Точки пересечения с осью абсцисс находим из уравнения
х 3 - 2 х 2 + 2 х – 1 = 0
Решим кубическое уравнение, для этого найдем один из корней.
При х = 1 получаем верное равенство, т.е. 13 -2∙12 + 2∙1 – 1 = 0.
Разделим х 3 - 2 х 2 + 2 х – 1 на х – 1:
 х 3 - 2 х 2 + 2 х – 1 х – 1
х 3 - 2 х 2 + 2 х – 1 х – 1
х3 - х2 х 2 – х + 1
– х 2 + 2 х – 1
– х 2 + х
х – 1
х – 1
х 3 - 2 х 2 + 2 х – 1 = (х - 1)(х 2 – х + 1).
Решим уравнение (х - 1)(х 2 – х + 1) = 0, х - 1 = 0 или х 2 – х + 1 = 0,
х = 1 D = - 3 < 0
Итак, функция проходит через точки (0; - 1) и (1; 0).
3. Исследуем функцию на четность, изменив знак аргумента на противоположный: у (- х)=(- х)3 – 2(- х)2 + 2(- х) – 1 = - х 3 - 2 х 2 - 2 х – 1 = - (х 3 + 2 х 2 + 2 х + 1)  у (х).
у (х).
Получили совсем другую функцию, значит, исходная функция является функцией общего вида.
4. Функция является непрерывной, значит, нет вертикальных асимптот. Проверим, есть ли наклонная асимптота вида у = kx + b. Для этого найдем угловой коэффициент прямой:
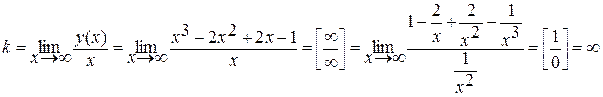 Отсюда следует, что наклонной асимптоты нет.
Отсюда следует, что наклонной асимптоты нет.
5. Найдем интервалы монотонности. Вычислим производную и приравняем ее к нулю:
у ' = (х 3 - 2 х 2 +2 х – 1) = 3 х 2 - 4 х +2 = 0. Из уравнения 3 х 2 - 4 х +2 = 0 найдем критические точки: D = - 8 < 0. Критических точек нет, функция монотонно возрастает на всей области определения.
6. Точек экстремума нет.
7. Найдем интервалы выпуклости и точки перегиба графика функции, если они есть. Вычислим вторую производную и приравняем ее к нулю:
у"= (3 х 2 - 4 х +2) = 6 х – 4 = 0. Из уравнения 6 х – 4 = 0 найдем точки, подозрительные на перегиб: 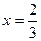 .
.
| Х | 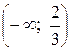
| 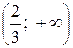
|
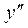
|  – –
|  + +
|
| У |
1.  На основании проведенного исследования построим график функции
На основании проведенного исследования построим график функции
у
- 1 0 1 х
- 1
№ 7.
1) Вычислить интеграл 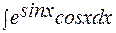 .
.
Решение
Данный интеграл вычисляется методом замены переменной.
Имеем:
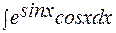 =
=  =
= 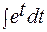 = e
= e 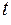 + C = e
+ C = e  +C.
+C.
Проверка
Если интеграл вычислен верно, то производная e  +C должна равняться подынтегральной функции
+C должна равняться подынтегральной функции 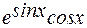 .
.
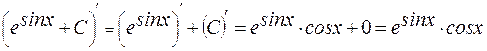 .
.
Вычислить интеграл  .
.
Решение
Данный интеграл вычисляется методом замены переменной.
Имеем:
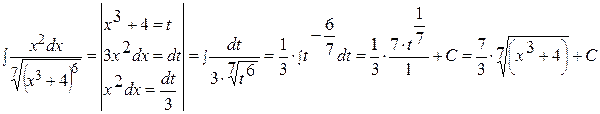 .
.
Проверка
Если интеграл вычислен верно, то производная 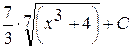 должна равняться подынтегральной функции
должна равняться подынтегральной функции 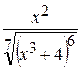 .
.
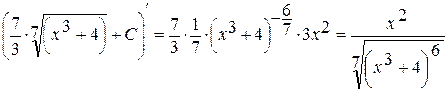 .
.
2) Вычислить интеграл  .
.
Решение
Под знаком интеграла неправильная дробь; выделим целую часть путем деления числителя на знаменатель.
 =
= 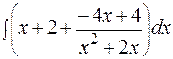
(разложим правильную рациональную дробь на простейшие дроби)
 ,
,
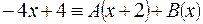 , т.е.
, т.е.
 .
.
Отсюда следует, что

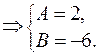
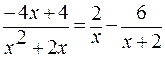 и
и 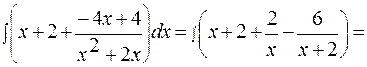
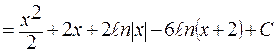 .
.
Проверка
Найдем производную выражения 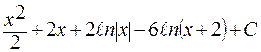 .
.
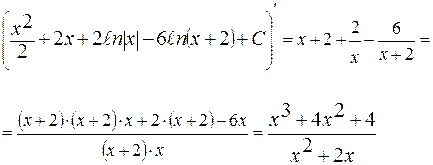 .
.
Интеграл вычислен правильно, так как производная первообразной равна подынтегральной функции.
№ 8. Вычислить интеграл 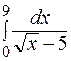 .
.
Решение
При вычислении определенных интегралов используются такие же методы, что и при вычислении неопределенных интегралов, но не стоит забывать о пределах интегрирования.
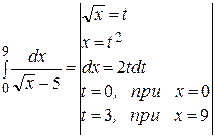 =
= 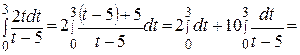
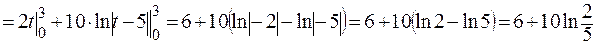 .
.
Решить задачу с использованием классического определения
Вероятности.
1) В урне содержатся 5 белых и 4 черных шара. Наудачу вынимают 2 шара. Найти вероятность того, что: а) оба шара белые; б) хотя бы один из них черный.
Решение:
а) 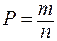 .
.
 . Т.к. должны появиться следующие шары:
. Т.к. должны появиться следующие шары: 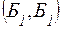 ,
, 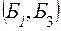 ,
,  ,
,  и т.д.
и т.д.
 . Т.к. должны появиться следующие шары:
. Т.к. должны появиться следующие шары:  ,
,  ,
, 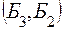 ,
, 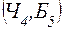 и т.д.
и т.д.
Поэтому 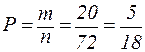 .
.
б)  . Т.к. должны появиться следующие шары:
. Т.к. должны появиться следующие шары:  ,
,  ,
,  ,
, 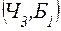 ,
, 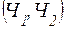 ,
, 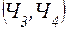 и т.д.
и т.д.
 .
.
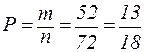 .
.
2) В коробке 5 синих, 4 красных и 3 зеленых карандаша. Наудачу вынимают 3 карандаша. Какова вероятность того, что: а) все они одного цвета; б) все они разных цветов; в) среди них 2 синих и 1 зеленый карандаш?
Решение:
а) Выбрать 3 синих карандаша из 5 можно 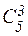 ; 3 красных карандаша из имеющихся четырех можно выбрать
; 3 красных карандаша из имеющихся четырех можно выбрать 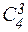 способами; 3 зеленых из 3 зеленых -
способами; 3 зеленых из 3 зеленых - 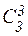 способами.
способами.
Следовательно, по правилу сложения, 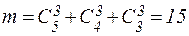 .
.
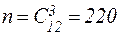 .
.
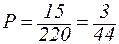 .
.
б) По правилу умножения число элементарных исходов, благоприятствующих событию, равно  .
.
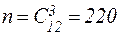 .
.
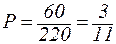 .
.
в) По правилу умножения 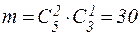 .
.
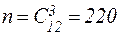 .
.
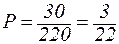 .
.
3) Дано 6 карточек с буквами Н, М, И, Я, Л, О. Найти вероятность того, что получится слово МОЛНИЯ, если наугад одна за другой выбираются 6 карточек и располагаются в ряд в порядке появления.
Решение:
Шестибуквенные «слова» отличаются друг от друга лишь порядком расположения букв (НОЛМИЯ, ЯНОЛИМ, ОЛНИЯМ и т.д.). Их число равно числу перестановок из 6 букв, т.е. 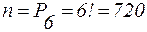 . Тогда вероятность появления слова молния равна
. Тогда вероятность появления слова молния равна 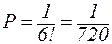 .
.
№ 2. Решить задачу с использованием теорем сложения и умножения вероятностей.
1) В корзине находится 13 деталей, из них 7 стандартные. Из корзины наудачу берут последовательно (сначала одну, потом другую) две детали, не возвращая их обратно. Найти вероятность того, что обе детали стандартны.
Решение
Пусть событие С – обе взятые детали стандартные.
Событие С – сложное и состоит из двух простых событий А и В.
Сформулируем простые события А и В: событие А – первая взятая деталь стандартная; событие В – вторая взятая деталь стандартная.
Для того, чтобы наступило событие С, необходимо, чтобы события А и В произошли одновременно, следовательно, 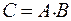 .
.
События А и В являются зависимыми, значит, для нахождения вероятности события С воспользуемся теоремой произведения вероятностей зависимых событий:
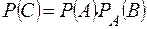 .
.
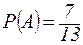 ,
,  .
.
Тогда  .
.
2) Вероятность выхода из строя станка в течение одного рабочего дня равна 0,01. Какова вероятность того, что за 5 дней станок ни разу не выйдет из строя?
Решение
Вероятность того, что станок выйдет из строя в течение дня, равна 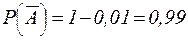 . Тогда по теореме умножения вероятностей
. Тогда по теореме умножения вероятностей  - вероятность того, что станок не выйдет из строя в течение 5 дней.
- вероятность того, что станок не выйдет из строя в течение 5 дней.
3) В ящике а белых и b черных шаров. Какова вероятность того, что из двух вынутых шаров один белый, а другой черный? (Вынутый шар в урну не возвращается).
Решение. Пусть:
событие А – появление белого шара при первом вынимании;
событие В – появление черного шара при втором вынимании;
событие С – появление черного шара при первом вынимании;
событие D – появление белого шара при втором вынимании.
Вычислим вероятность того, что первый вынутый шар белый, а второй черный:  .
.
Найдем вероятность того, что первый вынутый шар черный, а второй белый:
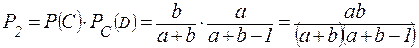 .
.
Таким образом, вероятность того, что один из вынутых шаров белый, а другой – черный, определится по теореме сложения:  , т.е.
, т.е.
 .
.
№ 3. Решить задачу с использованием формулы Бернулли.
1) В урне 20 шаров: 15 белых и 5 черных. Вынули подряд 5 шаров, причем каждый вынутый шар возвращается в урну и перед извлечением следующего шары в урне тщательно перемешиваются. Найти вероятность того, что из пяти вынутых шаров будет два белых шара.
Решение.
Вероятность появления белого шара в каждом испытании равна 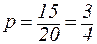 , а вероятность не появления белого шара равна
, а вероятность не появления белого шара равна 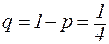 . По формуле Бернулли находим:
. По формуле Бернулли находим: 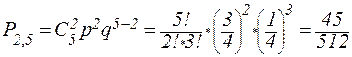 .
.
№ 4. Решить задачу и использованием формулы полной вероятности или формула Байеса.
1) Имеются три одинаковые по виду урны. В первой урне 15 белых шаров, во второй – 10 белых и 5 черных, а в третьей – 15 черных шаров. Из выбранной наугад урны вынули белый шар. Найти вероятность того, что шар вынут из первой урны.
Решение.
Событие А – появление белого шара;
гипотеза 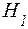 - выбор первой урны;
- выбор первой урны;
гипотеза  - выбор второй урны;
- выбор второй урны;
гипотеза  - выбор третьей урны.
- выбор третьей урны.
Имеем: 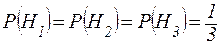 ,
,  ,
, 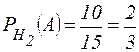 ,
,  .
.
Искомую вероятность 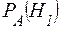 находим по формуле Байеса:
находим по формуле Байеса:
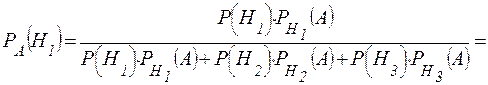
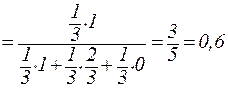 .
.






