Проводники и диэлектрики в электростатическом поле

Проводник – вещество, содержащее достаточное количество свободных зарядов. Обычно проводник не заряжен, так как в любом физически бесконечно малом объеме находятся равные количества положительных и отрицательных зарядов. Попадая в электрическое поле (рис.24), заряды начинают перемещаться под действием электрических сил, и возникает поле наведенных зарядов (электризация через влияние или электростатическая индукция). Результирующая напряженность , если заряды покоятся, так как в противном случае продолжалось бы их перераспределение.

Диэлектрики различают с жесткими и с квазиупругими диполями. Диполь (рис.25) характеризуется плечом , направленным от минуса к плюсу, и дипольным моментом . Если для данного диэлектрика величина постоянная (в не очень сильных полях), то диполи называются жесткими. Если — линейная функция напряженности, то диполи квазиупруги.

Диэлектрик в отсутствие электрического поля электронейтрален, так как в любом физически бесконечно малом объеме векторная сумма дипольных моментов равна нулю (из-за хаотичности расположения молекул).

При наложении электрического поля напряженности на электронные оболочки молекул диэлектрика с жесткими диполями действуют механические моменты, стремящиеся развернуть дипольные моменты вдоль поля (рис.26). Под действием этих моментов повернутся вдоль поля некоторые дипольные моменты (не все и не точно вдоль поля), т.е. будет наблюдаться преимущественная ориентация дипольных моментов (рис. 27). В диэлектрике с квазиупругими диполями дипольный момент молекулы в отсутствие внешнего поля равен нулю. Это можно представить себе, если заменить все движущиеся электроны молекулы одним неподвижным отрицательным зарядом, а все ядра – эквивалентным положительным зарядом. Такие центры положительных и отрицательных зарядов молекулы в отсутствие внешнего поля могут совпадать. Внешнее поле «растаскивает» эти центры в противоположные стороны, тем самым наводя дипольный момент каждой молекулы (рис.28). Процесс появления преимущественной ориентации диполей называется поляризацией диэлектрика. Поляризация диэлектрика с жесткими диполями называется ориентационной (рис.27), поляризация диэлектрика с квазиупругими диполями электронной поляризацией смещения (рис.29).

Для характеристики степени поляризации вводится вектор поляризации – векторная сумма дипольных моментов молекул, содержащихся в единице объема диэлектрика:

.

где n – число диполей физически бесконечно малого объема D V.

В любом физически бесконечно малом объеме внутри однородного диэлектрика будет одинаковое количество положительных и отрицательных полюсов молекул. Поэтому в таком диэлектрике невозможен объемный заряд. На граничных поверхностях появляются поляризационные заряды и, следовательно, появляется наведенное поле, характеризующееся напряженностью (рис.30). Напряженность результирующего поля не равна нулю (если бы она стала равной нулю, дезориентация диполей немедленно повлекла бы за собой уменьшение ).

При увеличении внешнего поля дипольный момент каждой молекулы диэлектрика с квазиупругими диполями растет пропорционально напряженности:

, ,

где n ₀ – концентрация молекул; диэлектрическая восприимчивость. Итак,

.

Аналогичная формула справедлива и для диэлектрика с жесткими диполями, так как степень ориентации диполей возрастает при увеличении напряженности поля.

Диэлектрическая восприимчивость b – величина, численно равная вектору поляризации данного вещества (деленному на e₀) в поле единичной напряженности.

Рассмотрим элемент диэлектрика в электрическом поле (рис.31). Этот элемент представляет собой диполь с зарядами 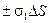, где ±s¢ – поверхностная плотность поляризационного заряда. Дипольный момент этого диполя является векторной суммой дипольных моментов молекул этого элемента 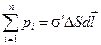. Отсюда вектор поляризации . Следовательно, . Если образующая элемента не параллельна вектору , то это равенство справедливо для нормальной составляющей вектора поляризации:

.

Нормальная составляющая вектора поляризации численно равна поверхностной плотности поляризационных зарядов. Умножив формулу для напряженности результирующего поля почленно на e₀, получим:

, но

( – напряженность поля в вакууме). По теореме Гаусса – Остроградского для поля плоского конденсатора только связанных зарядов (см. рис.31) . Вектор смещения поля только поляризационных зарядов (если представить, что только поляризационные заряды создают поле в вакууме). Но . Так как (см. рис.30) вектора и противоположно направлены . Таким образом, получаем:

или

Выясняется, что вектор характеризует поле свободных зарядов (или поле в вакууме); вектор – поле связанных (поляризационных) зарядов; вектор – суммарное поле (результирующее поле в каждой точке данной среды).

(квазиупругие или жесткие диполи). Согласно формуле для вектора смещения

.

Приравнивая коэффициенты и раскрывая, получаем:

.

Диэлектрическая проницаемость вещества так же, как диэлектрическая восприимчивость, характеризует поляризуемость диэлектрика.

 

Контрольная работа № 1-2

 

Номер варианта	Номера заданий
	1-1	1-15	1-26	1-30	2-1	2-10	2-25	2-31	2-43	2-50
	1-2	1-16	1-27	1-35	1-43	2-2	2-17	2-24	2-31	2-44
	1-3	1-17	1-28	1-36	1-44	2-3	2-18	2-23	2-32	2-45
	1-4	1-18	1-29	1-37	1-49	2-4	2-10	2-22	2-38	2-46
	1-5	1-19	1-30	1-40	1-48	2-7	2-19	2-21	2-38	2-47
	1-6	1-14	1-20	1-31	1-41	2-5	2-15	2-20	2-48	2-50
	1-7	1-13	1-21	1-32	1-46	2-6	2-19	2-25	2-39	2-49
	1-8	1-12	1-22	1-33	1-47	2-8	2-18	2-30	2-47	2-50
	1-9	1-11	1-23	1-34	1-45	2-9	2-17	2-27	2-33	2-41
	1-2	1-10	1-24	1-35	1-48	2-16	2-26	2-34	2-40	2-49
	1-11	1-14	1-25	1-36	1-44	2-11	2-15	2-28	2-35	2-48
	1-6	1-12	1-16	1-29	1-37	2-5	2-13	2-29	2-37	2-46
	1-4	1-13	1-17	1-27	1-38	2-14	2-28	2-30	2-39	2-45
	1-1	1-14	1-20	1-39	1-42	2-2	2-12	2-21	2-31	2-41
	1-12	1-15	1-22	1-39	1-41	2-3	2-11	2-23	2-32	2-42
	1-3	1-16	1-31	1-40	2-1	2-10	2-13	2-26	2-33	2-43
	1-10	1-17	1-28	1-34	1-42	2-2	2-9	2-24	2-34	2-34
	1-9	1-18	1-26	1-33	1-43	2-8	2-11	2-20	2-35	2-40
	1-8	1-19	1-27	1-38	1-44	2-7	2-14	2-22	2-36	2-47
	1-5	1-20	1-32	1-45	2-5	2-9	2-16	2-27	2-37	2-41
	1-6	1-11	1-21	1-34	1-46	2-6	2-16	2-25	2-38	2-45
	1-8	1-22	1-33	1-45	1-47	2-3	2-12	2-28	2-39	2-42
	1-4	1-14	1-23	1-38	1-48	2-4	2-17	2-29	2-36	2-40
	1-7	1-18	1-24	1-39	1-49	2-1	2-8	2-28	2-41	2-43
	1-2	1-15	1-25	1-3	1-40	2-4	2-15	2-27	2-36	2-42

 

 

Контрольная работа №1

1.1. Шарик падает с высоты 1 м на небольшую наклонную плоскость, расположенную под углом 45° к горизонту. Найти скорость шарика через 2 с после удара его о плоскость. Удар считать упругим, происходящим без вращения шарика, сопротивление воздуха не учитывать.

1-2. Со скалы над морем брошен камень в горизонтальном направлении. Через 4,04 с был увиден всплеск от падения камня, а через 4,34 с услышан звук падения камня. Считать скорость распространения звука равной 333 м/с, определить: а) дальность полета камня; б) высоту скалы; в) скорость, с которой был брошен камень; г) скорость в момент падения камня. Сопротивлением воздуха пренебречь.

1-3. Камень брошен с вышки в горизонтальном направлении со скоростью 20 м/с. Определить скорость, а также тангенциальное и нормальное ускорения камня в конце второй секунды после начала движения.

1-4. Наибольшая высота подъема тела, брошенного под углом к горизонту со скоростью 20 м/с, составляет 10 м. Под каким углом оно брошено?

1-5. Материальная точка движется по окружности, диаметр которой равен 40 м. Зависимость пути от времени ее движения определяется уравнением s = t³ + 4t² - t+8. Определить пройденный путь, скорость, нормальное, тангенциальное и полное ускорения через 39 с от начала движения точки по окружности. Построить векторную диаграмму скорости и ускорения.

1-6. Точка равномерно движется в вертикальной плоскости по окружности радиусом 0,2 м с угловой скоростью w=10 с^-1. Составить уравнение движения проекции точки на вертикальный диаметр. Начальный угол, отсчитанный от горизонтального диаметра, равен p/4. Найти зависимость ускорения от времени.

1-7. Точка движется по окружности радиусом 60 см с тангенциальным ускорением 10 м/с². Чему равны нормальное и полное ускорения в конце третьей секунды после начала движения? Чему равен угол между векторами полного и нормального ускорений в этот момент?

1-8. Снаряд массой 20 кг летит под углом 60° к горизонту со скоростью 200 м/с. В наивысшей точке подъема он встретил цель и полностью погасил скорость в течение 0,02 с. Определить среднюю силу удара. Сопротивление воздуха не учитывать.

1-9. Средняя высота спутника над поверхностью Земли равна 1700 км. Определить его скорость и период обращения, если радиус Земли равен 6400 км.

1-10. Какое нормальное ускорение должен иметь искусственный спутник на высоте, равной половине земного радиуса, чтобы он мог обращаться вокруг Земли по окружности?

1-11. Найти изменение ускорения свободного падения тела с изменением глубины от поверхности Земли. На какой глубине это ускорение составит 0,3 от ускорения на поверхности Земли? Плотность Земли считать постоянной. Учесть, что со стороны вышележащего сферического слоя тело не испытывает никакого притяжения.

1-12. Маховик начал вращаться равноускоренно из состояния покоя и, сделав 16 полных оборотов, приобрел угловую скорость, соответствующую 8 оборотам в секунду. Определить угловое ускорение маховика и продолжительность равноускоренного вращения.

1-13. Четыре груза весом 250 Н каждый закреплены на крестообразном маятнике на расстоянии 20 см от оси вращения и приводятся во вращение посредством гири весом 900 Н. Гиря привязана к концу веревки, намотанной на находящийся на той же оси шкив радиусом 10 см и падает под действием собственного веса. Через сколько времени скорость вращения маятника достигнет 540 об/мин? Какую скорость будет иметь гиря, когда она опускается на 2,5 м?

1-14. Диск весом 150 Н и радиусом 20 см вращался по инерции, делая 10 об/с. Через 5 с после начала торможения диск остановился. Найти момент тормозящей силы.

1-15.Сплошной однородный диск массой 250 г насажен на вал, радиус которого 0,2 см. Диск подвешен на двух параллельных нитях, намотанных на вал (маятник Максвелла). Момент инерции диска вместе с валом относительно оси вала 2490 г×см². Если опустить диск, то он будет падать вниз под действием силы тяжести, а натяжение нитей приведет его во вращательное движение. Определить ускорение поступательного движения диска.

1-16. С какой высоты должен скатиться по желобу шарик, чтобы он мог описать замкнутую петлю радиусом 4 м?

1-17. Маховик, массу которого, равную 50 кг, можно считать равномерно распределенной по окружности радиуса 70 см, вращается, делая 10 об/с. Вследствие трения, скорость вращения его уменьшилась до 5 об/с в течении 25 с. Определить тормозящий момент сил трения и число оборотов, сделанных маховиком за это время.

1-18. Обруч массой 5 кг катится без скольжения с постоянной скоростью 14 м/с. Определить: а) кинетическую энергию обруча; б) через сколько времени обруч остановится, если сила трения равна 50 Н?

1-19. Цилиндр массой 7 кг катится без скольжения с постоянной скоростью 19 м/с. Определить: а) кинетическую энергию цилиндра; б) через сколько времени цилиндр остановится, если сила трения равна 50 Н?

1-20.Шар массой 6 кг катится без скольжения с постоянной скоростью 15 м/с. Определить: а)кинетическую энергию шара; б) через сколько времени шар остановится, если сила трения равна 50 Н.

1-21. Какой скоростью должен обладать цилиндр, катящийся без скольжения, чтобы подняться по наклонной плоскости, составляющей с горизонтом угол 30°, на высоту 1,5 м, если сила трения равна 0,4 силы давления цилиндра на плоскость? Сколько времени будет продолжаться подъем?

1-22. Какой скоростью будет обладать цилиндр после скатывания с наклонной плоскости высотой 1,5 м и углом наклона 30°, если сила трения равна 0,4 силы давления цилиндра на плоскость? Сколько времени он будет скатываться?

1-23. Тело массой 10 кг брошено под углом 45° к горизонту. Какова была начальная скорость, если в наивысшей точке подъема кинетическая энергия тела была равна 100 Дж? Сопротивлением воздуха пренебречь.

1-24.Стержень массой 1,5 кг и длиной 0,5 м может вращаться около оси, проходящей через его середину перпендикулярно стержню. В конец стержня попадает пуля массой 10 г, летящая перпендикулярно к оси и к стержню со скоростью 300 м/с. Определить угловую скорость, которую получит стержень, если пуля застрянет в нем.

1-25. В подвешенный мешок с песком весом 50,1 Н ударилась пуля массой 10 г. При этом мешок откачнулся на высоту 10 см. Определить скорость пули при ударе.

1-26. Человек, сидя в неподвижной лодке, бросает на берег груз весом 100 Н со скоростью 7 м/с относительно берега. Определить вес лодки с человеком, если лодка отплыла на 2 м, а сила трения лодки о воду равна 10 Н.

1-27. Стальной стержень падает с высоты 19,5 м и своим концом ударяется об абсолютно твердую поверхность. Считая, что вся энергия, выделившаяся при ударе, пошла на деформацию стержня, определить его относительное укорочение.

1-28. С высоты 50 см на наклонную плоскость, расположенную под углом 30° к горизонту, падает шарик массой 50 г. Считая удар шарика упругим и происходящим без вращения, найти силу его удара о плоскость. Продолжительность удара равна 0,1 с.

1-29. Скорости двух центрально соударяющихся шаров равны 0,1 и 0,05 м/с, их массы соответственно равны 4 и 3 кг. Определить скорости после удара при неупругом соударении.

1-30.Скорости двух центрально соударяющихся шаров равны 0,1 и 0,05 м/с, их массы соответственно равны 4 и 3 кг. Определить скорости после удара при соударении.

1-31.Какое растягивающее напряжение нужно приложить к стальному стержню, чтобы получить такое же относительное удлинение, как при нагревании на 100°С?

1-32. Какую работу нужно совершить, чтобы растянуть на 1 мм стальной стержень длиной 1 м и сечением 1 мм²?

1-33. Какую силу надо приложить к стальной проволоке длиной 5 м и диаметром 2 мм, чтобы растянуть ее на 1 см? Определить напряжение материала растянутой проволоки и работу растяжения.

1-34. Определить длину стальной проволоки площадью поперечного сечения 10^-6 м², если сила в 1,96´10² Н растягивает ее на 10^-3 м.

1-35. Тело А движется вверх по наклонной плоскости под действием груза В. Коэффициент трения k=0,05, угол наклона a=30°. Определить ускорение движения тела А, если вес его и груза В одинаков и равен 50 Н. (рисунок).

1-36. Груз лежит на наклонной плоскости, составляющей с горизонтом угол 30°. На груз действует сила, направленная параллельно наклонной плоскости. Коэффициент трения груза по плоскости равен 0,1. Определить во сколько раз приложенная сила меньше веса груза, если груз движется равномерно вверх?

1-37. Вагонетка начинает подниматься вверх по наклонной плоскости, составляющей с горизонтом угол 45°. Коэффициент трения колес вагонетки о рельсы 0,02. Начальная скорость 10 м/с. Определить: 1) на какую высоту поднимется вагонетка; 2)сколько времени будет продолжается подъем; 3)с какой скоростью вагонетка скатится обратно?

1-38. Вал радиусом 20 см и весом 200 Н вращается по инерции, делая 5 об/с. К цилиндрической поверхности вала прижали тормозную колодку с силой 80 Н. Через 20 с вал остановился. Определить коэффициент трения.

1-39. Тонкий стержень длиной 0,5 м и массой 1 кг колеблется в вертикальной плоскости около горизонтальной оси, проходящей через конец стержня. Насколько изменится частота колебаний стержня, если ось опустить вниз на 10 см от верхнего конца?

1-40. Два маятника в одном и том же месте Земли за одинаковое время совершают один 30, а второй 40 колебаний. Какова длина каждого маятника, если разность их длин 0,07 м?

1-41. Тонкий прямой стержень совершает гармонические колебания около горизонтальной оси, проходящей через его конец. Какова длина стержня, если он делает 39 полных колебаний в минуту.

1-42. К пружине подвешен груз. Зная, что максимальная кинетическая энергия колебаний груза равна 1 Дж, найти коэффициент деформации пружины. Амплитуда колебаний 0,05 м.

1-43. Точка участвует в двух взаимно перпендикулярных колебаниях. Одного периода с одинаковыми начальными фазами. Амплитуда колебаний 20 и 21 мм. Найти амплитуду результирующего колебания.

1-44. Тело массой 20 г совершает гармоническое колебание с амплитудой 5 см и частотой 100 Гц. Определить кинетическую, потенциальную и полную энергии колеблющегося тела в момент, когда смещение равно половине амплитуды.

1-45. Груз, подвешенный к пружине, колеблется с амплитудой 1 см. Чему равна максимальная кинетическая энергия груза, если коэффициент упругости пружины 10 Н/см?

1-46. Частота колебаний тела 20 Гц. В какие моменты времени потенциальная энергия колебаний в четыре раза меньше кинетической? Уравнение колебаний считать синусоидальным, начальную фазу принять равной p/2.

1-47. Написать уравнение гармонического колебания тела при условии, что кинетическая энергия колебаний тела в момент времени 0,0125 с в 4 раза больше потенциальной энергии; период колебаний равен 0,05 с, амплитуда колебаний – 0,2м.

1-48. Уравнение гармонического колебания тела массой 0,2 кг записывается так: . За сколько времени кинетическая энергия тела уменьшится от 0,2 до 0,1 Дж?

1-49. Стальной и медный стержни приведены в соприкосновение своими торцами. Как изменится скорость звука при переходе из стали в медь?

Контрольная работа №2

2-1. Сколько молекул газа находится в сосуде емкостью 15 л при нормальных условиях?

2-2. Сколько киломолей и молекул содержится в сосуде емкостью 250 см³, если газ находится в нем при давлении 566 мм.рт.ст. и температуре 10°С?

2-3. В сосуде емкостью 40 л находится гелий при температуре 24°С. Произошла утечка газа и давление в нем снизилось на 2 атм.Какое количество газа было потеряно? Температуру газа считать постоянной.

2-4. Каков молекулярный вес газа, если он при температуре 27°С и давлении 2 атм имеет плотность, равную 2,6 г/л?

2-5. В закрытом сосуде емкостью 2 м³ находятся 1,4 кг азота и 2 кг кислорода. Определить температуру газовой смеси, если давление смеси равно 1,4×10⁵ Н/м ².

2-6. Какой объем занимает смесь 1 кг кислорода и 2 кг гелия при нормальных условиях?

2-7. Баллон емкостью 20 л содержит смесь азота и гелия при тем­пературе 47°С и давлении 15 атм. Определить массу как азота, так и гелия, если их общая масса равна 250 г.

2-8. Воздух состоит из 76% азота, 23% кислорода и 1% аргона. Определить кажущийся или средний молекулярный вес воздуха. Молекулярный вес аргона 40 г/моль.

2-9. Определить температуру газа, если средняя кинетическая энергия поступательного движения одной молекулы равна 6,9 ´10^-21 Дж.

2-10. Средняя кинетическая энергия поступательного движения отдельных молекул газа равна 5×10^-14 эрг, число молекул в 1 см³составляет 3×10¹⁹. Определить давление газа.

2-11. Баллон объемом 0,1 м³ содержит 150 г кислорода при давлении 1,25 атм. Определить суммарную кинетическую энергию поступательного движения молекул газа в джоулях.

2-12. Определить среднюю кинетическую энергию поступательного и вращательного движения одной молекулы водяного пара при температуре 150° С.

2-13. Сколько молекул содержится в 1 см³ газа, при давлении 10^-5 мм.рт.ст. и температуре 15°С?

2-14. Определить число Лошмидта, т. е. число молекул, содержащихся в 1 см³ при нормальных условиях.

2-15. В колбе емкостью 200 см³ находится газ при температуре 47°С. Из-за утечки газа из колбы просочилось 10²¹ молекул. На сколько снизится давление в колбе (в мм.рт.ст.)?

2-16. Определить давление, оказываемое водородом на стенки со­суда, если средняя арифметическая скорость молекул газа 1850 м/си в 1 см³ находится 3×10²⁰ молекул.

2-17. При какой температуре молекулы кислорода имеют такую же среднюю квадратичную скорость, как и молекулы азота при t=7⁰ С?

2-18. Баллон емкостью 8 л содержит 2 кг газа при давлении 5 атм. Определить среднюю квадратичную, среднюю арифметическую и наиболее вероятную скорости молекул газа.

2-19. В воздухе при t = 27°С находятся молекулы водорода и взве­шенные мельчайшие пылинки массой 10 ^-8 г. Определить среднюю квадратичную скорость молекул водорода и пылинок, а также их среднюю Кинетическую энергию поступательного движения.

2-20. Определить среднюю длину свободного пробега молекул, если в сосуде емкостью 5 л находится 1 г кислорода.

2-21. Определить среднюю длину свободного пробега молекул азо­та, если плотность разреженного газа 1,8×10 ^-6 кг/м³.

2-22. Определить коэффициент диффузии и коэффициент теплопроводности водорода, находящегося при температуре 0°С и давле­ний 760 мм.рт.ст.

2-23. Сколько соударений в секунду в среднем испытывают, молекулы азота при температуре 0 °С и давлении 760 мм рт. ст.

2-24. Подсчитать молярные и удельные теплоемкости C _ри C _vуглекислого газа, считая его идеальным газом.

2-25. Определить молярные и удельные теплоемкости С _р и С _v кислорода, считая его идеальным газом.

2-26. Масса кислорода,100 г. При постоянном давлении он был нагрет на 30°. Определить работу расширения газа.

2-27. Определить работу расширения 1 кмоль азота, если ему передано 1000 Дж тепла и он расширяется при постоянном давлении.

2-28. Какое количество тепла необходимо подвести к системе, чтобы нагреть 220 г углекислого газа на 20°: а) при постоянном объеме; б) при постоянном давлении?

2-29. При расширении 1 кмоль кислорода была совершена работа в 1000 Дж. Рассчитайте тепловые затраты при изотермическом и изобарическом процессах. Почему при изотермическом расширении газа на ту же работу затрачивается меньшее количество тепла?

2-30. Семь граммов азота при температуре 37° С расширили до тройного объема. Определить работу расширения газа при изотермическом и адиабатическом процессах.

2-31. Сколько выделится тепла, если кислород, занимающий объем 16 л при давлении 5 атм, сжать до объема, равного 4 л. Изотермически, изобарически? Почему в одном случае тепла выделится больше?

2-32. Кислород, находящийся под давлением 100 атм, адиабатически расширился, так, что его объем увеличился в 16 раз. Определить давление кислорода после расширения.

2-33. Определить изменение энтропии 4 кг расплавленного свинца, взятого при температуре плавления, при охлаждении до 0°С? (t_пл =327°С).

2-34. Определить прирост энтропии при превращении 100 г льда при t = -30°С в пар.

2-35. В результате изобарического расширения объем 5 г водорода увеличился с 5 до 10 л. Определить изменение энтропии газа.

2-36. Определить работу идеальной тепловой машины за один цикл, если она в течение цикла получает от нагревателя 500 кал тепла. Температура нагревателя 400° К, температура холодильника 300⁰К.

2-37. Температура нагревателя тепловой машины, работающей по циклу Карно, 207⁰С, а температура холодильника 117°С. Какова должна быть температура нагревателя (при неизменной температуре холодильника), чтобы К.П.Д. машины увеличился в 3 раза?

2-38. За счет каждой килокалории тепла, полученной от нагревателя тепловой машины, работающей по циклу Карно, машина совершает работу, равную 1700 Дж. Определить температуру нагревателя и тепловой, машины, если температура охладителя равна 280° К.

2-39. В цилиндре под поршнем находится газовая смесь, воспламеняющаяся при температуре 927° С. Смесь быстро сжимается до воспламенения. Во сколько раз нужно уменьшить объем смеси, чтобы она воспламенилась, если начальная температура смеси 27° С? Считать процесс адиабатическим и k =1,5.

2-40. Найти постоянные а и b в уравнении Ван-дер-Ваальса для углекислого газа и их наименование, если для него Т_к равно 304 К и р_к равно 73 атм.

2-41. Один моль гелия занимает объем 2 л при температуре 27⁰С. Определить давление гелия, пользуясь уравнением Ван-дер-Ваальса. Для гелия критическая температура 5,2 К и критическое давление 2,25 атм.

2-42. Критическая температура для воды 374,3 К, критическое давление 2256 Н/см². Написать уравнение Ван-дер-Ваальса для водяного пара.

2-43. В одной и той же капиллярной трубке вода поднимается на 50 мм, а керосин на 26 мм. Определить коэффициент поверхностного натяжения керосина. Коэффициент поверхностного натяжения воды 0,071 Н/м.

2-44. Спирт, коэффициент поверхностного натяжения которого 0,022 Н/м налит в U-образную трубку. Определить разность диаметров каналов в коленах трубки, если разность уровней спирта составляет 1 см. Плотность спирта равна 800 кг/м³.

2-45. На какую высоту поднимается вода между двумя плоскопараллельными стеклянными пластинками, если расстояние между ними равно 1 мм? Коэффициент поверхностного натяжения воды равен 0,071 Н/м.

2-46. Объем 24 капель воды, вытекающей из капиллярной трубки, равен 1см³. Определить диаметр отверстия трубки, зная, что диаметр шейки капли и диаметр отверстия трубки одинаковы. Коэффициент поверхностного натяжения воды равен 0,071 Н/м.

2-47. U-образный сосуд налита ртуть, плотность которой при 20⁰С равна 13,6 г/см³. Колена сосуда представляют собой капилляры с диаметрами 0,1 и 1,0 мм. Разность уровней ртути составляет 15 см. Найти коэффициент поверхностного натяжения ртути.

2-48. Определить и молекулярный вес газа, если скорость распространения звука равна 333 м/с, а средняя квадратичная скорость движения молекул газа равна 484,5 м/с при t=0⁰С.

2-49. Определить , если скорость распространения звука в газе при нормальном давлении 1260 м/с, а плотность его равна 0,09 кг/м³.

2-50. Зная скорость звука в гелии 968 м/с, вычислить скорость звука в водороде при той же температуре.

 

Розв‘язування кінематичних задач по темі: “Кінематика поступального, криволінійного та обертального руху матеріальної точки.”

Задача 1 Із точки з координатами x ₀, y ₀ кинуто тіло під кутом a₀ до горизонту з початковою швідкістю . Знайти:

1. положення і швидкість тіла через час t;

2. рівняння траєкторії польоту тіла ;

3. нормальне і тангенціальне прискорення тіла;

4. радіус кривизни траєкторії в момент часу t;

5. повний час польоту;

6. найбільшу висоту підйому;

7. кут, під яким треба кинути тіло, щоб висота його підйому дорівнювала далекості польоту (при умові, що );

8. найбільшу далекість польоту;

Направимо осі X iY вздовж горизонтального та вертикального переміщення точки. Векторні рівняння руху тіла:

Для знаходження положення тіла в момент часу t знайдемо проекції на осі координат:

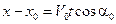
Якщо спроектувати друге векторне рівняння на осі координат, можна знайти складові швидкості:

Тоді результуюча швидкість .

Тангенс кута між напрямком результуючої швидкості та вісі X дорівнює

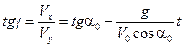, тобто він змінюється протягом часу t. Це й зрозуміло, оскільки швидкість геометрично характеризується нахилом дотичної до траєкторії польоту

Щоб визначити тангенціальне та нормальне прискорення тіла в точці з координатами x, y замітимо, що повне прискорення тіла весь час направлено вниз і являє собою прискорення сили тяжіння .

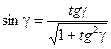Тангенціальне прискорення дорівнює проекції вектора на дотичну до траєкторії (тобто , що видно з рисунку), а нормальне прискорення дорівнює проекції – на нормаль, тобто

; , то ,

Знайдемо приблизне значення радіуса кривизни (R) траєкторії в момент часу t. Приймаючи, що точка рухається по дузі кола, скористуємося формулою 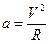, звідки .

Найбільшу далекість польоту 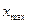знайдемо за умови . Якщо в рівнянні траєкторії прийняти , то одержамо квадратне рівняння, з якого можна знайти : . Якщо тіло кинуте з точки на поверхні де і , то задача значно спрощується. Скорочуючи на 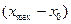, знаходимо, що . Загальний час польоту можна визначити із формули при , звідки

Найбільшої висоти підйому тіло досягає в момент часу t, коли 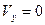. Враховуючи що складова швидкості вздовж осі Y дорівнює , то при : .

Тепер скористаємося рівнянням проекції положення тіла на вісь Y, прийнявши : 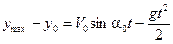. Виключаючи t з обох рівнянь, одержимо . Очевидно що найбільша висота підйому буде при , тобто коли тіло кинуте вертикально вгору.

Прирівнявши та один одному (при умові, що , ), одержимо

, звідки ;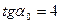

Знайдемо швидкість тіла в момент приземлення (при умові, що , ).

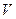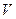Для цього підставимо значення у виразі для швидкостей та , а також у формулу для кута між і віссю X.

При цьому одержимо: ; ; ;

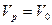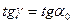
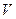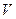Ми бачимо, що вертикальна складова швидкості тіла протягом часу польоту змінюється від до нуля, а потім до . Горизонтальна складова залишається сталою і дорівнює . Таким чином модуль швидкості в польоті весь час змінюється. Змінюється також і напрямок швидкості, в зв‘язку з тим що кута між і віссю X зменшується від до нуля (в точці максимального підйому) і потім до (в точці приземлення).