Рассмотрим поле какого-либо вектора 
, определенного в каждой точке своего поля. Линиями этого вектора называются линии, касательные к которым совпадают с вектором в каждой точке. Линии приписывают направление, совпадающее с направлением вектора. Условимся проводить через каждую единичную площадку, перпендикулярную линиям , количество линий, равное значению этого вектора в данной точке. Если поле неоднородно, выбирают элементарную площадку dS 0, перпендикулярную линиям, настолько малой, чтобы во всех ее точках вектор можно было считать одинаковым (в пределе – бесконечно малой):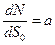 
, где dN – число линии, проведенных через нормальную площадку dS 0. Потоком линий вектора через произвольную поверхность S называется число линий вектора, проходящих сквозь эту поверхность (если они проведены по сформулированному выше правилу). Элементарный поток 
. Выберем элементарную площадку dS, не перпендикулярную линиям вектора , так, чтобы ее пронизывал тот же элементарный поток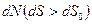 
. Из рис.19 
. Следовательно, 
. Введем новый вектор 
, где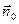 
– единичный вектор нормали к площадке dS. Тогда
,
так как a – угол между и 
(см. рис.19). Поток линий вектора через конечную поверхность S
.
Поток через замкнутую поверхность или полный поток линий вектора
.
В векторе использован единичный вектор внешней нормали. Таким образом, полный поток – алгебраическая величина. Выходящие из замкнутой поверхности линии считаются со знаком плюс (
), входящие – со знаком минус (
).
Аналогично линиям напряженности электрического поля вводятся линии вектора смещения.
Поток этих линий через произвольную площадку S
.
Сосчитаем полный поток линий вектора смещения через замкнутую сферическую поверхность, в центре которой расположен точечный заряд Q 0, создающий поле (рис.20):
.
Как видим, полный поток линий вектора смещения не зависит от формы поверхности и от того, где внутри нее расположен заряд (рис.21).
Линии вектора 
пересекают поверхность S нечетное число раз, причем, кроме одного, с попарно противоположными знаками (входят, выходят). Поэтому в поток линий вектора каждая линия войдет один раз со знаком, определяемым ее направлением. Значит, полный поток вектора смещения через любую замкнутую поверхность, охватывающую создающий поле заряд, равен этому заряду: 
.
Здесь – вектор смещения на элементе поверхности dS (рис.21). Пусть теперь поле создано n зарядами (рис.22). Для каждого из зарядов Q 0, попавших внутрь мысленной поверхности S, можно написать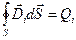 
, где 
– вектор смещения поля i -го заряда в точках dS. Для каждого из зарядов, не попавших внутрь этой поверхности (рис.23), 
(четное число пересечений линий с поверхностью). Суммируя все такие уравнения почленно, имеем:
.
где k – число зарядов, охваченных поверхностью S. Иначе 
.
Вынесем общий для всех членов суммы элемент dS за знак суммирования: 
. Здесь все векторы относятся к одному элементу поверхности dS. По принципу суперпозиции полей вектор смещения результирующего поля 
, где n – число всех зарядов, создающих поле в данной точке (а не только охваченных поверхностью). Получаем теорему Гаусса – Остроградского
или 
.
Полный поток линий вектора смещения через любую (замкнутую) поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью.
Если в поле можно выбрать какую-либо замкнутую поверхность, через которую не равен нулю поток линий соответствующего вектора, эти линии не замкнуты. То, что такую замкнутую поверхность можно выбрать сколь угодно близкой к заряду (и охватывающей его), доказывает, что точки, в которых находятся заряды, – особые точки поля (вспомним, что для этих точек теряют смысл все характеристики поля: 
; ; j и т.д.), заряды — его источники, как и предполагалось ранее. Линии напряженности электростатического поля и линии вектора смещения начинаются и заканчиваются на зарядах (или в бесконечности).
Теорема Гаусса – Остроградского во многих случаях позволяет рассчитать вектор смещения в данной точке электрического поля. Для этого надо мысленную поверхность S провести через точку, в которой определяется вектор . Поверхность выбирается так, чтобы, по возможности, проще разрешалось уравнение относительно искомого вектора , лучше всего, если на всей поверхности или на конечном числе ее частей вектор постоянен и составляет постоянный угол с нормалью к поверхности. В тех случаях, когда применение теоремы не встречает непреодолимых математических трудностей, рассчитывают вектор , вектор , затем потенциал, т.е. сравнительно просто получают важнейшие характеристики данной точки электростатического поля.
Например, для бесконечной равномерно заряженной плоскости 
, где 
– поверхностная плотность зарядов. Для поля плоского конденсатора 
.
