Цель работы:
1. Дать представление о финансовых функциях, описать их возможности.
2. Показать возможность расчета суммы вклада и стоимости инвестиции, расчета величины и продолжительности процентных платежей.
3. Рассмотреть финансовые функции для анализа инвестиций, для расчета амортизационных отчислений при использовании различных методик расчета амортизации.
Финансовые функции используют в планово-экономических расчетах. Всего в категории "Финансовые" имеется 53 функции. Среди полного перечня финансовых функций выделяется группа функций, используемая для анализа инвестиций и расчета операций по кредитам, ссудам и займам.
Таблица 2 - Назначение и форматы финансовых функций для анализа инвестиций
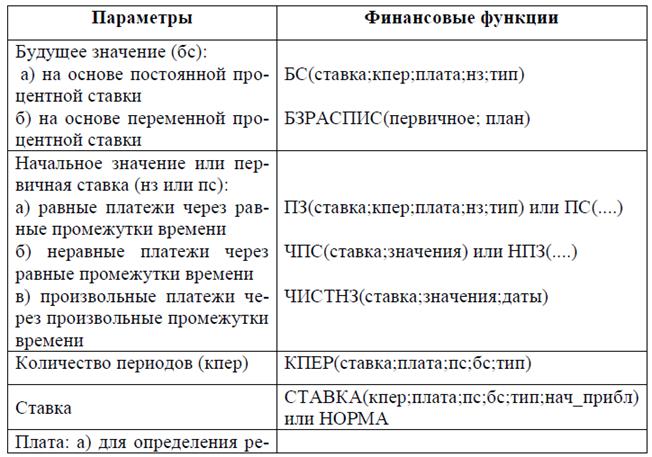
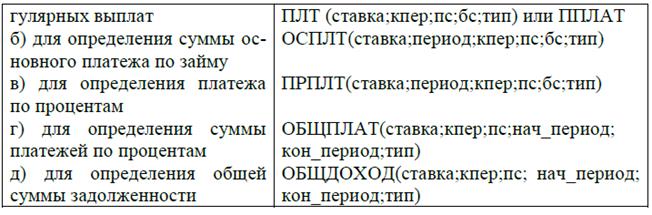
Особенности использования финансовых функций:
При создании формул следует устанавливать одинаковую размерность периода для процентной ставки и числа платежей. Например, если платежи производятся один раз в год, то и процентная ставка должна быть дана в годовом исчислении, если платежи производятся ежемесячно, то должна быть задана месячная процентная ставка.
Все аргументы, означающие денежные средства, которые должны быть выплачены (например сберегательные вклады), представляются отрицательными числами; денежные средства, которые должны быть получены (например дивиденды), представляются положительными числами.
Рассмотрим примеры решения следующих задач, связанных с расчетом операций по кредитам, ссудам и займам:
· определение наращенной стоимости (будущей стоимости);
· определение начального значения (текущей стоимости);
· определение срока платежа и процентной ставки;
· расчет периодических платежей, связанных с погашением займов.
Пример 1. 1) Необходимо рассчитать будущую сумму вклада в размере 1000 руб., внесенного на 10 лет с ежегодным начислением 10% (рис. 6.1.), и будущую сумму вклада при тех же условиях, но с ежегодным внесением 1000 руб. (рис.6.2.).
2) Требуется рассчитать, какую сумму можно занять на 8 лет под 6% годовых, если есть возможность выплачивать ежемесячно по 200 руб.
Решение.
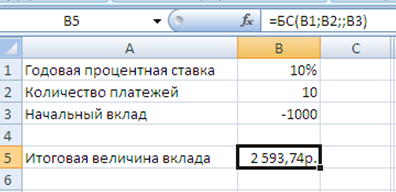
Рисунок 6.1. - Расчет величины вклада с начальным взносом
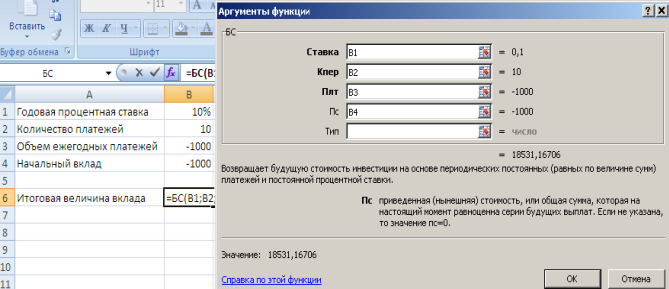
Рисунок 6.2. - Расчет величины вклада с начальным взносом при регулярном пополнении
Результат вычисления: в первом случае - 2593,74 руб., во втором - 18531,17руб.
Эту же функцию БС можно использовать и для расчета величины возможного займа.
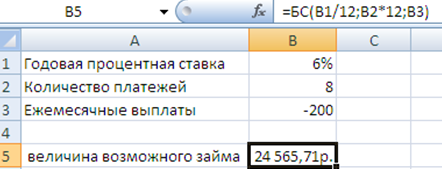
Рисунок 6.3. - Расчет величины возможного займа при помощи функции БС
Пример 2. Необходимо:
1) рассчитать величину вложения под 10 % годовых, которое будет ежегодно в течение 10 лет приносить доход 1000 руб.
2) рассчитать величину вложения под 10 % годовых, которое через 10 лет принесет доход 10000 руб.
Решение: 1)
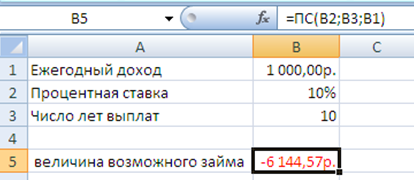
Рисунок 6.4. - Расчет стоимости инвестиции
Результат вычисления получается отрицательным (-6 144,57 руб.), поскольку эту сумму необходимо заплатить. 2)
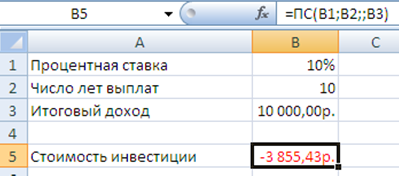
Рисунок 6.5. - Расчет стоимости инвестиции.
Результат вычисления получается отрицательным (-3855,43 руб.), поскольку эту сумму необходимо заплатить.
Пример3. Необходимо рассчитать величину ежемесячного вложения под 6 % годовых, которое через 12 лет составит сумму вклада 50000 руб.
Решение.
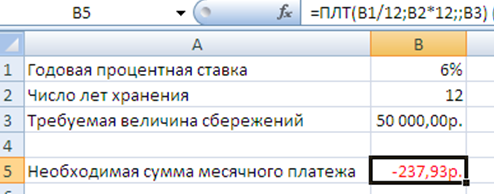
Рисунок 6.6. - Расчет процентных платежей.
Результат вычисления получается отрицательным (-237,95 руб.), поскольку эту сумму необходимо выплачивать.
При тех же условиях, но с начальным вкладом 10000 руб.
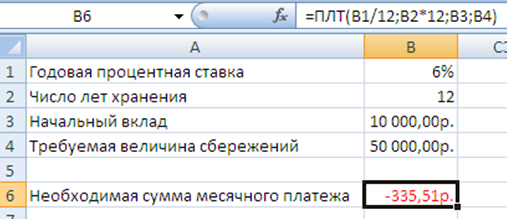
Рисунок 6.7. - Расчет процентных платежей
Результат вычисления получается отрицательным (-335,51 руб.), поскольку эту сумму необходимо выплачивать.
Эту же формулу (рис. 6.7.) можно использовать и при расчете платежей по займу. Например, необходимо рассчитать величину ежемесячной выплаты по займу в 50000 руб. под 6 % годовых на 12 лет. Результат будет тот же самый -237,95 руб.
Пример 4. Необходимо рассчитать количество ежемесячных платежей для погашения займа в 10000 руб., полученного под 10 % годовых, при условии ежемесячной выплаты 200 руб.
Решение.

Рисунок 6.14. Расчет количества платежей с использованием функции КПЕР. Результат вычисления – 42 ежемесячные выплаты.
Список задач.
1. На банковский счет под 11,5% годовых внесли 37000 руб. Определить размер вклада по истечении трех лет, если проценты начисляются каждые полгода.
2. Определить сколько денег окажется на банковском счете, если ежегодно в течение пяти лет под 17% годовых вносится 20000 руб. Взносы осуществляются в начале каждого года.
3. Достаточно ли положить на счет 85000 руб. для приобретения через пять лет легкового автомобиля стоимостью 160 000 руб.? Банк начисляет проценты ежеквартально, годовая ставка 12%. Определить необходимую сумму (с помощью «подбора параметра»).
4. По облигации номиналом 50000 руб., выпущенной на 6 лет, предусмотрен следующий порядок начисления процентов: в первый год – 10%, в следующие два года – 20%, в оставшиеся три года – 25%. Определить будущую стоимость облигации с учетом переменной процентной ставки.
5. По облигации, выпущенной на шесть лет, предусмотрен порядок начисления процентов, приведенный в задаче 4. Рассчитать номинал облигации, если известно, что ее будущая стоимость составила 216562,50 руб.
6. Фирме требуется 500 000 руб. через три года. Определить, какую сумму необходимо внести фирме сейчас, чтобы к концу третьего года вклад увеличился до 500 000 руб., если процентная ставка составляет 12% годовых.
7. Клиент заключает с банком договор о выплате ему в течение пяти лет ежегодной ренты в размере 5000 руб. в конце каждого года. Какую сумму необходимо внести клиенту в начале первого года, чтобы обеспечить эту ренту, исходя из годовой процентной ставки 20%?
8. Пусть инвестиции в проект к концу первого года его реализации составят 20000 руб. В последующие четыре года ожидаются годовые доходы по проекту: 6000 руб., 8200руб., 12600р. и 18800 руб. Рассчитать чистую текущую стоимость проекта к началу первого года, если процентная ставка составляет 10% годовых. 9. Инвестор с целью инвестирования рассматривает два проекта, рассчитанные на пять лет. Проекты характеризуются следующими данными:
· По первому проекту – начальные инвестиции составляют 550 000 руб., ожидаемые доходы за пять лет соответственно 100 000, 190 000, 270 000, 300 000 и 350 000 руб.;
· По второму проекту – начальные инвестиции составляют 650 000 руб., ожидаемые доходы за пять лет соответственно 150 000, 230 000,470 000,180 000 и 320 000 руб.
Определить, какой проект является наиболее привлекательным для инвестора при ставке банковского процента – 15% годовых.
10. Определите чистую текущую стоимость по проекту на 05.04.2005 при ставке дисконтирования 8%, если затраты по нему на 05.08.2005 со-ставят 90 млн. руб., а ожидаемые доходы в течение следующих месяцев будут: 10 млн. руб. на 10.01.2006; 10 млн. руб. на 10.01.2006; 20 млн. руб. на 01.03.2006; 30 млн. руб. на 15.04.2006; 40 млн. руб. на 25.07.2006.
11. Рассчитать через сколько лет вклад размером 100 000 руб. достигнет 1 000 000 руб., если годовая процентная ставка по вкладу 13,5% и начисление процентов производится ежеквартально.
12. Для покрытия будущих расходов фирма создает фонд. Средства в фонд поступают в виде годовой ренты в конце года. Сумма разового пла-тежа 16 000 руб. На поступившие взносы начисляются 11,2% годовых. Необходимо определить, когда величина фонда будет равна 100 000 руб.
13. Предположим, что для получения через два года суммы в 1 000 000 руб. предприятие готово вложить 250 000 руб. сразу и затем каждый месяц по 25 000 руб. Определить годовую процентную ставку.
14. Выдан кредит 500 000 руб. на 2,5 года. Проценты начисляются раз в полгода. Определить величину процентной ставки за период, если известно, что возврат составит 700 000 руб.
15. Клиент банка осуществляет заем в размере 5000 руб. под 6% годовых на 6 месяцев. Определите ежемесячные платежи клиента. Платежи осуществляются в конце месяца.
16. Клиенту банка необходимо накопить 200 000 руб. за два года. Клиент обязуется вносить в начале каждого месяца постоянную сумму под 9% годовых. Какой должна быть эта сумма?
17. Определите платежи по процентам за первый месяц от трехгодичного займа в 100 000 руб. из расчета 10% годовых.
18. Клиент ежегодно в течение пяти лет вносил деньги на свой счет в банке и накопил 40000 руб. Определите, какой доход получил клиент банка за последний год, если годовая ставка составила 13,5%.
19. Определите значение основного платежа для первого месяца двухгодичного займа в 60000 руб. под 12% годовых.
20. Организация взяла ссуду в банке в размере 500 000 руб. на 10 лет под 10,5% годовых, проценты начисляются ежемесячно. Определите сумму выплат по процентам за первый месяц и за третий год периода.
21. Ссуда размером 1 000 000 руб. выдана под 13% годовых сроком на три года; проценты начисляются ежеквартально. Определите величину общих выплат по займу за второй год.
22. Банком выдан кредит в 500 000 руб. под 10% годовых сроком на три года. Кредит должен быть погашен равными долями, выплачиваемыми в конце каждого года. Разработать план погашения кредита, представив его в виде следующей таблицы:

23. Рассчитать сумму процентов, начисленных на вклад в 750 000 тыс. руб. за два года, если банк начисляет проценты ежеквартально из расчета 28% годовых. Какова должна быть годовая депозитная ставка, если за два года необходимо удвоить первоначальный вклад.
24. Потребитель получает заем на покупку автомобиля 20 000$ под 8% годовых сроком на три года при ежемесячных выплатах. Какова будет сумма по процентам и основной платеж за первый и последний месяцы выплат?
25. Потребитель занимает сумму 250 000$, подлежащую выплате в течение 10 лет при 12% годовых на ежемесячной основе. Какова сумма процента и основного капитала на первом году займа?
26. Кредит в сумме 5 000 000 руб. предоставлен под 20% годовых сроком на 10 лет. Рассчитайте величину остатка основной суммы без учета
выплаченных процентов на начало третьего года.






