Шбұрыштар.
1.Үшбұрыштың периметрі 36 см, ал қабырғаларының ұзындықтарының қатынасы 2:3:4 қатынасындай. Үшбұрыштың қабырғаларын табыңдар.
А) 8;9;19; В) 10;6;20; С) 7;12;17; Д)10;12;14; Е) 8;12;16
2.АВС бұрышы шеңберге іштей сызылған. Оған сәйкес центрлік бұрыш 880. АВС бұрышын табыңдар.
А) 470; В) 450; С) 460; Д) 440; Е) 420
3. АВС үшбұрышында ЕD кесіндісі АС қабырғасына параллель орта сызығы болсын. ВЕD үшбұрышында  Берілген үшбұрыштың бұрыштарын табыңдар.
Берілген үшбұрыштың бұрыштарын табыңдар.
А)  ; В)
; В)  ; С)
; С) 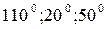
Д)  ; Е)
; Е) 
4. Үшбұрыштың сыртқы бұрышы 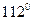 -қа тең. Осы бұрышпен сыбайлас емес екі ішкі бұрыштың бірі
-қа тең. Осы бұрышпен сыбайлас емес екі ішкі бұрыштың бірі  . Үшбұрыштың ішкі бұрыштарын есептеңіз.
. Үшбұрыштың ішкі бұрыштарын есептеңіз.
А)  ; В)
; В)  ; С)
; С) 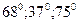
Д)  ; Е)
; Е) 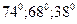
5.Тең бүйірлі үшбұрыштың табанындағы сыртқы бұрышының шамасы  .Үшбұрыштың барлық бұрыштарын табыңыз:
.Үшбұрыштың барлық бұрыштарын табыңыз:
А)  ; В)
; В)  ; С)
; С) 
Д)  ; Е)
; Е) 
6.Үшбұрыштың бұрыштары 3:7:8 сандарына пропорционал. Үшбұрыштың ең үлкен бұрышын табыңыз.
А) 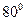 ; В)
; В)  ; С)
; С)  ; Д)
; Д)  ; Е)
; Е) 
7.Үшбұрыштың бұрыштары 7:5:6 сандарына пропорционал. үшбұрыштың ең кіші бұрышын табыңыз.
А)  ; В)
; В)  ; С)
; С)  ; Д)
; Д)  ; Е)
; Е) 
Квадрат. Тіктөртбұрыш.
1 Квадраттың диагоналы 6 см-ге тең. Оның ауданың табыңыз.
А) 24 см2; В) 16 см2; С) 18 см2; Д) 36 см2; Е) 12 см2
2. Квадраттың периметрі 24 см болса, оның қабырғасын табыңыз:
А) 8 см; В)  см; С)
см; С)  см; Д) 4 см; Е) 6 см
см; Д) 4 см; Е) 6 см
3.Тіктөртбұрыштың периметрі 56 см, ал бір қабырғасы келесінен 6 есе ұзын. Тіктөртбұрыштың ауданын табыңыз.
А) 144 см2; В) 48 см2; С) 196 см2; Д) 112 см2; Е) 96 см2
4.Диагоналі 10 см тең квадраттың қабырғасын табыңдар.
А)  см; В) 5см; С)
см; В) 5см; С)  см; Д)
см; Д) 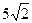 см; Е)
см; Е)  см
см
5.ABCD тік төртбұрышында 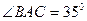 . Тік төртбұрыштың диагональдарының арасындағы бұрышты табыңдар.
. Тік төртбұрыштың диагональдарының арасындағы бұрышты табыңдар.
А)  ; В)
; В)  ; С)
; С)  ; Д)
; Д)  ; Е)
; Е) 
6. Квадраттың диагоналі 10 см болса, квадраттың ауданын табыңыз.
А) 100см2; В) 64 см2; С) 25 см2; Д) 36 см2; Е) 50 см2
Тест №9
Квадрат.Тіктөртбұрыш.
1.Тік төртбұрыштың ауданы 42см2. Егер оның ені 3 см болса, ұзындығы қанша болады?
А) 13 см; В) 11 см; С) 15 см; Д) 14 см; Е) 12 см
2.Квадраттың қабырғасы 9 см-ге тең.Ауданын табыңыз.
А) 81см2; В) 36 см2; С) 20,25 см2; Д) 72 см2; Е) 18 см2
3. Квадраттың диагоналі  см болса, квадрат қабырғасын табыңыз:
см болса, квадрат қабырғасын табыңыз:
А)  см; В)
см; В)  см; С) 6 см; Д) 4 см; Е) 3 см
см; С) 6 см; Д) 4 см; Е) 3 см
4.Бір қабырғасы 9 см, ал ауданы 108 см2 болатын тіктөртбұрыштың келесі қабырғасын табыңыз:
А) 42 см; В) 21 см; С) 45 см; Д) 36 см; Е) 12 см
5. Квадраттың диагоналі а-ға тең. Квадраттың қабырғасын табыңдар.
А)  ; В)
; В)  ; С)
; С)  ; Д) а; Е)
; Д) а; Е) 
6. Тік төртбұрыштың диагоналі оның қабырғаларының бірінен екі есе артық. Диагональдарының арасындағы бұрыштарын табыңдар.
А) 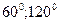 ; В)
; В)  ; С)
; С)  ; Д)
; Д)  ; Е)
; Е) 
7. Квадраттың ауданы 25 есе кемісе,онда оның қабырғалары
А) 5 есе артады; В) 5 есе кемиді; С) 10 есе артады
Д) 2 есе кемиді; Е) 10 есе кемиді.
8. Үшбұрыштың сыртқы екі бұрышы 100  -қа және 150
-қа және 150  -қа тең. Үшінші сыртқы бұрышын табыңдар.
-қа тең. Үшінші сыртқы бұрышын табыңдар.
А) 1800; В) 900; С) 3600; Д)450; Е) 1100
9. Тең қабырғалы үшбұрыштың ішкі және сыртқы бұрыштарын табыңдар.
А) 1000,800; В) 1350,450; С) 1100,700
Д) 600,1200; Е) 700,1100
10. Үшбұрыштың әрбір төбесінде неше сыртқы бұрыш болады?
А) 9; В) 1; С) 6; Д) 2; Е) 3
11. Тік төртбұрыштың периметрі 80см, ал қабырғаларының қатынасы 2:3 қатынасындай. Тік төртбұрыштың ауданын табыңдар.
A) 325 см2. B) 684см2. C) 384см2. D) 144см2. E) 524см2.
Алгебра
І нұсқа
1. Теңсіздікті графиктің көмегімен шешіңдер:
а) х2 − 7х – 5 < 0 ә) − х2 + 4х − 4 ≥ 0
2. Теңсіздікті шешіңдер:
а) (х – 1)(х + 2) > 0 ә) (х + 2)(х – 3) < 0
3. Интервалдар әдісімен теңсіздікті шешіңдер:
1) х2 – 7х + 6 < 0 2) (х + 3)(2х + 8) ≥ 0
х – 1
4. Теңсіддіктің оң шешімін қабылдайтын аралығын анықта:
 а)
а)
− 
 + −
+ −
х
− 1 2

 ә) + − + х
ә) + − + х

− 1/2 2
ІІ нұсқа
1. Теңсіздікті графиктің көмегімен шешіңдер:
а) z2 − 2z + 1 ≤ 0 ә) − t2 + 8t + 9 ≥ 0
2. Теңсіздікті шешіңдер:
а) (х – 5)(х − 4) > 0 ә) (х + 3)(х + 5) ≥ 0
3. Интервалдар әдісімен теңсіздікті шешіңдер:
1) х2 + 4х − 5 > 0 2) х2 – 3х – 4 ≤ 0
х – 3
4. Теңсіддіктің теріс шешімін қабылдайтын аралығын анықта:
 а)
а)

 + − +
+ − +
х
− 1 2

 ә) − + − х
ә) − + − х

− 3 5
І нұсқа
1. Теңдеулердің қайсысы квадрат теңдеу болады
1) 2х2 + 3х − 7 = 0; 2) х3 + 2х + 1 = 0 3) 1/2*х2 + 5 = 0
4) 4х2 + 6х = 0; 5) 3х4 + 11 = 0 6) 10х + 4 = 0
2. Теңдеуді шешіңдер:
1) х2 – 81 = 0 2) 3х2 = 27 3) 15х2 – 375 = 0
3. Теңдеудің шешімін табыңдар:
1) 2х2 + 5х + 4 = 0 2) 3х2 – 22х + 7 = 0
4. Берілген түбірлері бойынша квадрат теңдеу құрыңдар:
х1 = 7 және х2 = 8
5. Түбірлерінің қосындысы 3, көбейтіндісі − 2 болатын квадрат теңдеу құрыңдар
6. Теңдеудің түбірлерінің қосындысы мен көбейтіндісін табыңдар:
5х2 – 2х − 7 = 0
ІІ нұсқа
1. Теңдеулердің қайсысы квадрат теңдеу болады
1) 15х2 − 375 = 0; 2) х3 + 5х + 1 = 0 3) 2,5х2 − 3х + 7 = 0
4) 1/2*х2 − 7/2 = 0; 5) 5х4 + 3 = 0 6) 7х + 5 = 0
2. Теңдеуді шешіңдер:
1) х2 – 144 = 0 2) 2х2 = 8 3) 11х2 – 539 = 0
3. Теңдеудің шешімін табыңдар:
1) 3х2 − 5х − 2 = 0 2) 5х2 – 16х + 3 = 0
4. Берілген түбірлері бойынша квадрат теңдеу құрыңдар:
х1 = − 1,8 және х2 = 5
І нұсқа
1. Айнымалының қандай мәнінде
3х − 11 және х − 1
3х – 5 х + 2 бөлшектерінің көбейтіндісі 1-ге тең?
2. Биквадрат теңдеудің түбірлерін табыңдар:
1) х4 – х2 – 20 = 0 2) z4 − z2 − 6 = 0 3) х4 – 10х2 + 9 = 0
3. Тікбұрышты үшбұрыштың гипотенузасы 13 см-ге тең, катеттерінің бірі-екіншісінен 7 см-ге артық болса, онда тікбұрышты үшбұрыштың катеттерінің ұзындығын есептеңдер.
4. Теңдеуді шешіңдер:
1) 2х2 – 3х + 5 = 0 2) − 5х2 + 14х – 8 = 0
ІІ нұсқа
1. Айнымалының қандай мәнінде
5х + 1 және − 5х − 1
х2 – 9 3 – х бөлшектерінің бөліндісі 2-ге тең?
2. Биквадрат теңдеудің түбірлерін табыңдар:
1) х4 – 5х2 + 4 = 0 2) у4 − 6у2 + 9 = 0 3) z4 + 5z2 − 14 = 0
3. Егер тіктөртбұрыштың бір қабырғасы екіншісінен 4 см артық және ауданы 96 см2 болса, онда тіктөртбұрыштың қабырғаларын табыңдар.
4. Теңдеуді шешіңдер:
1) 4х2 – 2х + 13 = 0 2) − 7х2 + 13х – 6 = 0






