История открытия дружественных и совершенных чисел великими математиками

Таблица совершенных чисел

Совершенное число	Математик, открывший совершенное число	Значение p по формуле Евклида	Дата открытия	Кол-во цифр	Место открытия
					Др.Греция
					Др.Греция
	Евклид				Др.Греция
	Евклид				Др.Греция
			15 век
	Катальди				Италия
	Катальди				Италия

2305843009213693951∙2⁶⁰	Иван Михеевич Первушин		1883 г.		Пермь
618970019642690137449562111∙2⁸⁸			1911 г.
162259276829213363391578010288127∙2¹⁰⁶			1914 г.
2¹²⁶∙(2¹²⁷-1)			1914г.
2⁵²⁰∙(2⁵²¹-1)	Счетная машина		30 янв. 1952г		Калифорния
2⁶⁰⁶∙(2⁶⁰⁷-1)	Счетная машина		30 янв.1952г.		Калифорния
2¹²⁷⁸∙(2¹²⁷⁹-1)	Счетная машина		Июнь 1952г.		Калифорния
2²²⁰²∙(2²²⁰³-1)	Счетная машина		Октябрь 1952г.		Калифорния
2²²⁸⁰∙(2²²⁸¹-1)	Счетная машина		Октябрь 1952г.		Калифорния
2³²¹⁶∙(2³²¹⁷-1)	Г.Ризель		Сентябрь 1957г.	Около 2000	Швеция
2⁴²⁵²∙2⁴²⁵³-1)			1962г.
2⁴⁴²²∙(2⁴⁴²³-1)			1962г.
2⁹⁶⁸⁸∙(2⁹⁶⁸⁹-1)			1965г.
2⁹⁹⁴⁰∙(2⁹⁹⁴¹-1)			1965г.
2¹¹²¹²∙(2¹¹²¹³-10)			1965г.

Таблица дружественных чисел (меньше 100000)

Пара чисел	Математик(и), открывший(ие) пару дружественных чисел	Дата открытия
220 и 284	Пифагор	Около 500 до н.э.
1184 и 1210	Паганини
2620 и 2924	Эйлер
5020 и 5564	Эйлер
6232 и 6368	Эйлер
10744 и 10856	Эйлер
12285 и 14595	Браун
17296 и 18416	Аль-Банна	Около 1300
63020 и 76084	Эйлер
66928 и 66992	Эйлер
67095 и 71145	Эйлер
69615 и 87663	Эйлер
79750 и 88730	Рольф

Совершенные и дружественные числа. Числа близнецы.

История открытия дружественных и совершенных чисел великими математиками

Среди всех интересных натуральных чисел, издавна изучаемых математиками, особое место занимают совершенные и близко связанные с ними дружественные числа.

Числа 1, 2, 3, 4, 5…, использующиеся для счета предметов или для указания порядкового номера того или иного предмета среди однородных предметов, называются натуральными. Из огромного многообразия натуральных чисел ученые выделили дружественные и совершенные числа, обладающие рядом очень интересных свойств.

Дружественные числа – это два натуральных числа, для которых сумма всех делителей первого числа (кроме него самого) равна второму числу и сумма всех делителей второго числа (кроме него самого) равна первому числу. Дружественные числа были открыты последователями Пифагора. По свидетельству античного философа Ямвлиха, великий Пифагор на вопрос, кого считать своим другом, ответил: «Того, кто является моим вторым Я, как числа 220 и 284».

История дружественных чисел теряется в глубине веков. Эти удивительные числа были открыты последователями Пифагора. Правда пифагорейцы знали только одну пару дружественных чисел – 220 и 284. Проверим эту пару чисел на свойство дружественных чисел:

1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284, 1 + 2 + 4 + 71 + 142 = 220.

Для нахождения дружественных чисел арабский ученый Сабит ибн Курра (836-901) предложил хитроумный способ: задавшись натуральным числом n (n>1), подсчитать вспомогательные величины

p = 3 • 2^{n – 1} – 1, q = 3 • 2n – 1, r = 9 • 2^{2n – 1} – 1

Если окажется, что числа p, q, r простые, тогда числа А = 2ⁿpq и В = 2ⁿr – дружественные.
Но эта формула дает только 3 пары дружественных чисел: 220 и 284; 17296 и 184164; 9363584 и 9437056.
Пифагорова пара 220 и 284 получается по этому методу при n = 2. Следующую пару чисел – 17296 и 18416 – обнаружили независимо друг от друга марокканский ученый Ибн-аль-Банна (1256-1321), Фариси и три столетия спустя француз Пьер Ферма. В этом случае n = 4. Третью пару – 9363584 и 9437056 (при n = 7) – указал в 1638 г. Рене Декарт (1596-1650). Но дальнейшие попытки найти n к успеху не приводят. Более того, способ Сабита ибн Курры не выявляет ни одной пары дружественных чисел, если n увеличивать до 20000! Поэтому многие дружественные числа не могут быть получены по этой формуле.
Иногда частным случаем дружественных чисел считаются совершенные числа: каждое совершенное число дружественно себе. Никомах Герасский, знаменитый филосов и математик, писал: «Совершенные числа красивы. Но известно, что вещи редки и немногочисленны, безобразные встречаются в изобилии. Избыточными и недостаточными являются почти все числа, в то время как совершенных чисел немного» Но сколько их, Никомах, живший в первом столетии нашей эры не знал. Совершенным называется число, равное сумме всех своих делителей (включая 1, но исключая само число).
Первым прекрасным совершенным числом, о котором знали математики Древней Греции, было число «6». На шестом месте на званном пиру возлежал самый уважаемый, самый почетный гость. В библейских преданиях утверждается, что мир был создан в шесть дней, ведь более совершенного числа, среди совершенных чисел, чем «6», нет, поскольку оно первое среди них.
Рассмотрим число 6. Число имеет делители 1, 2, 3 и само число 6. Если сложить делители, отличные от самого числа 1 + 2 + 3 то мы получим 6. Значит, число 6 дружественно самому себе и является первым совершенным числом.
Следующим совершенным числом, известным древним, было «28». Мартин Гарднер усматривал в этом числе особый смысл. По его мнению, Луна обновляется за 28 суток, потому что число «28» – совершенное. В Риме в 1917 году при подземных работах было открыто странное сооружение: вокруг большого центрального зала расположены двадцать восемь келий. Это было здание неопифагорейской академии наук. В ней было двадцать восемь членов. До последнего времени столько же членов, часто просто по обычаю, причины которого давным-давно забыты, полагалось иметь во многих ученых обществах. До Евклида были известны только эти два совершенных числа, и никто не знал, существуют ли другие совершенные числа и сколько таких чисел вообще может быть. Великий основатель геометрии много занимался изучением свойств числа; конечно, его не могли интересовать совершенные числа. Евклид обнаружил, а Эйлер позднее строго доказал, что всякое число, которое может быть представлено в виде произведения множителей – 1, где 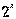– 1 – простое число, – совершенное число. Если в формулу Евклида подставить р = 2, то получим первое совершенное число: , а если подставить в нее р = 3, то получим второе совершенное число:

Проверим:

1 + 2 + 3 = 6 1 + 2 + 4 + 14 = 28

Благодаря своей формуле, Евклид сумел найти еще два совершенных числа: 496 (при р = 5) и 8128 (при р = 7). Почти полторы тысячи лет люди знали только четыре совершенных числа, и никто не знал, могут ли существовать еще числа, которые можно представить в евклидовской формуле, и никто не мог сказать, возможны ли совершенные числа, не удовлетворяющие формуле Евклида.