1. Скалярное произведение векторов – число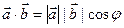 
; 1). проекция вектора на вектор 
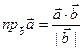; 2). если 
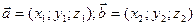, то 
.
Свойства: 1). 
; 2). 
; 3). скалярный квадрат 
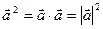, тогда 
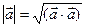; 4). 
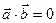; 5).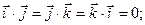 
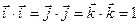. Условие перпендикулярности векторов: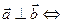 
.
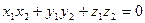Угол между векторами:
.
2. Векторное произведение - вектор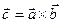 
, определяемый условиями:1). 
; 2). 
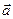перпендикулярен и 
, и 
; 3). вектор направлен так, что с его конца переход от первого сомножителя 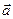ко второму виден как переход против часовой стрелки.
В координатах, если 
, 
, то
. 
.
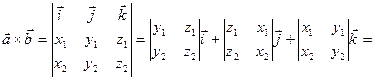
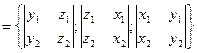Свойства векторного произведения: 1).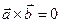 
; 2). 
; 3). 
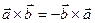; 4).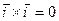 
, 
, 
; 
, 
, 
; 
, 
, 
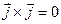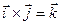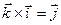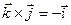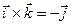. Геометрически модульвекторного произведения – площадь параллелограмма: 
.
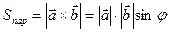3. Смешанное произведение векторов – число 
.
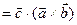Если 
; 
, то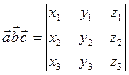 
.
Геометрически – объемы параллелепипеда и пирамиды: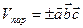 
, 
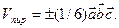
Условие компланарности векторов: 
.
Раздел 2. Аналитическая геометрия.
Простейшие задачи на плоскости.
Уравнение линии на плоскости 
.
Расстояние между двумя точками 
: 
.
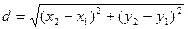Площадь треугольника ABC с вершинами в точках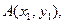 
:
.
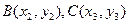Координаты точки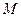 
, д елящий отрезок 
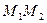в данном отношении 
:
.
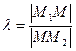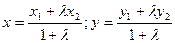Координаты середины отрезка (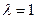
):
.
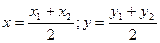Полярные координаты: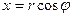 
, 
; 
, 
, 
.
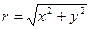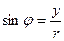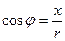Прямая на плоскости.
Уравнения прямой:
общее: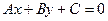 
, вектор 
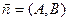перпендикулярен прямой;
с угловым коэффициентом: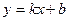 
;
проходящей через данную точку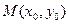 
с данным угловым коэффициентом 
: 
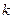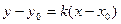; проходящей через две точки : 
;
в отрезках: 
.
Угол между двумя прямыми, заданными: общими уравнениям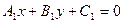и 
и 
:
;
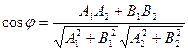уравнениями с угловым коэффициентом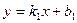 
, 
:
.
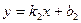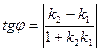Условия параллельности прямых: 
, 
.
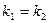Условия перпендикулярности прямых: 
, 
.
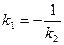Расстояние от точки 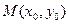до прямой :
.
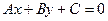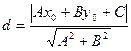Кривые 2 порядка.
Уравнение второго порядка 
задает: окружность при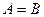 
; эллипс при 
; гиперболу при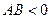 
; параболу, ес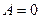ли 
или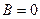 
. Уравнения окружности: с центром в т. 
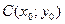и радиусом 
: 
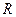; с центром в т.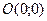 
: 
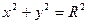. Каноническое уравнение эллипса: 
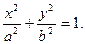Каноническое уравнение гиперболы: 
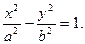Канонические уравнения параболы: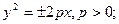 
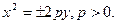
Плоскость в пространстве.
Уравнения плоскости:
проходящей через точку 
перпендикулярно вектору нормали 
:
;
общее:
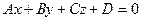; - вектор нормали;
в отрезках:
;
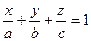проходящей через три данные точки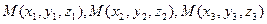 
:
.
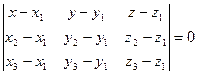Угол между плоскостями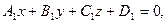 
:
.
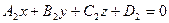Условие параллельности плоскостей: 
.
Условие перпендикулярности плоскостей 
.
Расстояние от точки 
до плоскости :
.
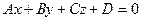Прямая в пространстве.
Уравнения прямой:
как линии пересечения двух плоскостей:
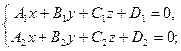
проходящей через точку параллельно вектору 
: 
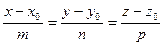- канонические уравнения прямой;
параметрические:
проходящей через две данные точки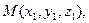 
:
.
Угол между прямыми:
.
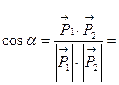
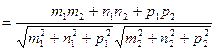Условие параллельности прямых: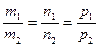 
.
Условие перпендикулярности прямых: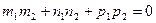 
.
Расстояние от точки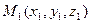 
до прямой :
.
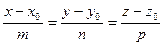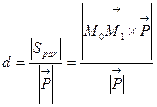Взаимное расположение плоскости и прямой в пространстве.
Условие параллельности прямой 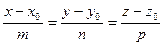и плоскости :
.
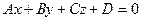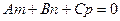Условие перпендикулярности прямой и плоскости:
.
Угол между прямой и плоскостью:
.
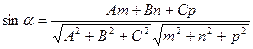Раздел 3. Пределы
Определенные выражения при нахождении пределов: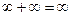 
; 
; 
; 
; 
; 
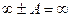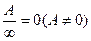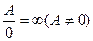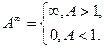
Неопределенности: 
, 
, 
, 
.
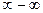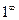