Определители.
1. Определитель второго порядка задается равенством
.
2. Определитель третьего порядка задается равенством
.
3. Свойства определителей. 1. Определитель равен нулю, если он содержит: две одинаковые или пропорциональные строки; строку (столбец) из нулей. 2. Определитель не изменится, если к любой его строке прибавить другую строку, умноженную на некоторое число. 3. Разложение определителя по любой строке (столбцу):
.
Способы вычисления определителя третьего порядка.
а). Правило Саррюса (дополнения): б). Правило треугольников:
в). Разложение определителя по первой строке:
.
Действия над матрицами. Обратная матрица.
1. Матрицей 
порядка 
называется прямоугольная таблица, составленная из действительных чисел и содержащая 
строк и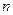 
столбцов:
.
2. Сумма (разность) матриц одного порядка 
= 
, 
.
3. Произведение матрицы на число 
.
4. Произведением 
матриц и 
называется матрица 
, элементы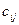 
которой равны сумме произведений соответствующих элементов 
-ой строки матрицы и 
-го столбца матрицы
:
.
При умножении матрицы порядка 
на матрицу порядка 
получится матрица порядка .
Некоммутативность (неперестановочность) умножения матриц: 
.
5. Если - невырожденная квадратная матрица (определитель матрицы 
), то существует единственная матрица 
, называемая обратной к матрице , такая, что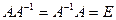 
, где 
- единичная матрица.
Чтобы найти необходимо: - вычислить определитель 
матрицы ; - найти алгебраические дополнения 
каждого элемента 
матрицы ; - составить из чисел матрицу 
; - транспонируя матрицу 
, составить матрицу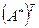 
; - умножить матрицу 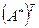на число 
: 
; - делаем проверку 
.
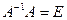Системы линейных алгебраических уравнений.
Система линейных уравнений третьего порядка имеет вид
1. Правило Крамера: если определитель матрицы системы не равен 0, то система имеет единственное решение, которое определяется по формулам
, 
, 
,
где 
определитель матрицы системы; 
определитель, получаемый из определителя 
заменой 
го столбца столбцом свободных членов, 
.
2. Матричный способ: система линейных уравнений в матричной форме имеет вид 
, где
, 
, 
.
Решение матричного уравнения определяется формулой 
.
3. Метод Гаусса заключается в последовательном исключении неизвестных из уравнений системы. Для краткости вместо системы рассматриваем расширенную матрицу ее коэффициентов, которую приводим к треугольному виду:
с помощью следующих, не меняющих решения, преобразований: 1. В 
можно менять местами строки.
2. Можно в менять местами столбцы слева от прямой черты. 3. К одной строке можно прибавить другую, умноженную на некоторое число.
Треугольную матрицу записываем в виде уравнений снизу вверх, последовательно находя неизвестные.
Векторы.
Вектором называется направленный отрезок.
Координаты вектора с началом в точке 
и концом в точке 
:
.
Длина вектора:
.
Проекция вектора на ось u: 
, 
- угол между осью 
и вектором 
. Направляющие косинусы: 
; 
; 
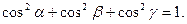Сумма (разность) векторов 
и 
: 
. Произведение вектора на число 
: 
.
Условие коллинеарности векторов: 
.
Разложение вектора 
по векторам 
: 
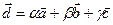, где 
- координаты вектора в системе координат 
.
