Предел числовой последовательности
Число А называется пределом числовой последовательности  , если для любого сколь угодно малого числа e > 0 найдется номер N > 0 такой, что для всех членов последовательности аn с номером n > N выполняется неравенство:
, если для любого сколь угодно малого числа e > 0 найдется номер N > 0 такой, что для всех членов последовательности аn с номером n > N выполняется неравенство: 
Обозначение предела: 
· Числовая последовательность, имеющая конечный предел, называется сходящейся, в противном случае – расходящейся.
· Числовая последовательность  называется бесконечно малой, если
называется бесконечно малой, если 
· Числовая последовательность  называется бесконечно большой, если для любого числа М > 0 найдется номер N такой, что для всех членов последовательности аn с номером n > N выполняется:
называется бесконечно большой, если для любого числа М > 0 найдется номер N такой, что для всех членов последовательности аn с номером n > N выполняется:  . Обозначение:
. Обозначение: 
……………………………………………………………………………………………………
Теорема 1.
1) Если  - бесконечно малая последовательность и все an ¹ 0, то
- бесконечно малая последовательность и все an ¹ 0, то  -
-
бесконечно большая последовательность.
2) Если  - бесконечно большая последовательность и все bn ¹ 0, то
- бесконечно большая последовательность и все bn ¹ 0, то  - бесконечно малая последовательность.
- бесконечно малая последовательность.
Формально эти утверждения выглядят так: 
Например, 
………………………………………………………………………………………………
Теорема 2 (о пределах последовательностей)
Если существуют пределы  , то
, то
1) существует 
2) существует 
3) существует 
…………………………………………………………………………………………………
Примеры.
Вычислим пределы, раскрывающие неопределенность вида  , пользуясь теоремами.
, пользуясь теоремами.

Для раскрытия неопределенности вида  использовали прием: числитель и знаменатель делим на старшую степень, т.е. на n2. Затем используются теоремы о пределах.
использовали прием: числитель и знаменатель делим на старшую степень, т.е. на n2. Затем используются теоремы о пределах.
2) 
3) 
Можно обобщить результаты:
Ø при равенстве старших степеней числителя и знаменателя в пределе всегда получается отношение числовых коэффициентов при этих старших степенях.
Ø если старшая степень числителя выше, то в пределе всегда получится бесконечность
Ø если старшая степень знаменателя выше, чем числителя, то в пределе всегда будет 0.
Пределы функции в точке
Пусть функция F(x) определена на множестве D.
· Число А называется пределом функции в точке х = х0, если для любого e >0 найдется число d >0 такое, что для всех х, удовлетворяющих неравенству 0<ôx - x0ô< d, выполняется неравенство ôF(x) -Aô< e
Обозначение: 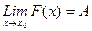
Для бесконечно малой в точке х0 функции: 
Для бесконечно большой в точке х0 функции: 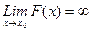
У функций существуют односторонние пределы:
· Левосторонний предел: 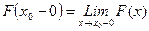
Число А называется пределом функции в точке х = х0 слева, если для любого e>0 найдется число d>0 такое, что для всех х, принадлежащих промежутку (х0 - d, х0), выполняется неравенство ôF(x) -Aô< e
· Правосторонний предел: 
Число А называется пределом функции в точке х = х0 справа, если для любого e>0 найдется число d>0 такое, что для всех х, принадлежащих промежутку (х0, х0+ d), выполняется неравенство ôF(x) -Aô< e
Например, 
Теорема 3 (о пределах функций)
Если существуют  , то
, то
1) существует 
2) существует 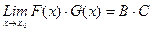
3) существует 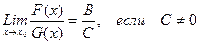
Примеры.
1) 
Этот пример решался непосредственно с помощью теорем о пределах, т.к. при подстановке х = 1 не возникало неопределенностей типа: 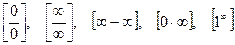 и т.п.
и т.п.
2)  В этом примере, в отличие от предыдущего, при подстановке числа 2 вместо х получаем неопределенность вида
В этом примере, в отличие от предыдущего, при подстановке числа 2 вместо х получаем неопределенность вида  , поэтому непосредственно применить теоремы о пределах нельзя. Необходим прием, избавляющий от неопределенности. Прием заключается в следующем: числитель и знаменатель раскладывают на множители, а затем сокращают множители, содержащие в себе эту неопределенность.
, поэтому непосредственно применить теоремы о пределах нельзя. Необходим прием, избавляющий от неопределенности. Прием заключается в следующем: числитель и знаменатель раскладывают на множители, а затем сокращают множители, содержащие в себе эту неопределенность.
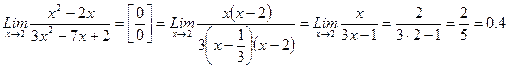
После сокращения множителя (х - 2) предел вычислялся непосредственной подстановкой
х = 2, т.е. с помощью теорем о пределах.
3)  - предел не содержит неопределенности и вычисляется непосредственной подстановкой.
- предел не содержит неопределенности и вычисляется непосредственной подстановкой.
4) 
5) 
6) 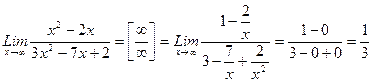
7) 
В данном примере прием, позволяющий избавиться от неопределенности – это домножение числителя и знаменателя на выражение, сопряженное выражению с корнем (отличается знаком). После этого, применив формулу разности квадратов, сокращаем множители, содержащие в себе неопределенность.
8)  - предел не содержит неопределенности и вычисляется непосредственной подстановкой х = 0.
- предел не содержит неопределенности и вычисляется непосредственной подстановкой х = 0.
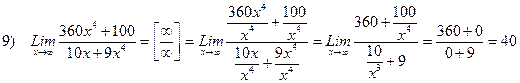

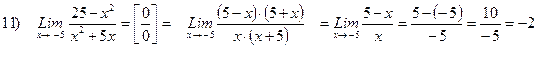
Для двух бесконечно малых или бесконечно больших функций существует понятие эквивалентности.
· Бесконечно малые или бесконечно большие в точке х0 функции a(х) и b(х) называются эквивалентными, если существует  .
.
Неопределенность, соответственно, 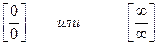
· Обозначение: 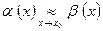
В этом случае справедливо следующее утверждение:
Теорема 4.
Если 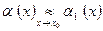 и
и  и существует
и существует  , то существует
, то существует  , причем пределы равны:
, причем пределы равны: 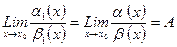
Например, 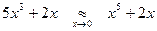 т.к.
т.к. 
 т.к.
т.к. 
Введем в рассмотрение 1-й замечательный предел:  .
.
Функция Sin x эквивалентна своему аргументу, если он бесконечно мал, т.е. в точке
х = 0.
Например, 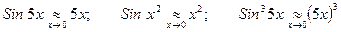
Легко получить еще два часто используемых предела:


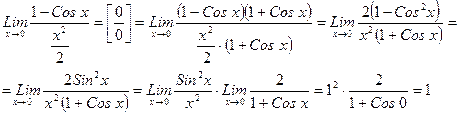
Таким образом, при вычислении пределов с тригонометрическими функциями, содержащими неопределенность вида  , можно использовать три основные эквивалентности:
, можно использовать три основные эквивалентности: 
Примеры.
1) 
2) 
3) 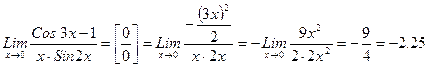
4) 
5) 
6) 
7)  - это не 1-й замечательный предел, т.к. аргумент не является
- это не 1-й замечательный предел, т.к. аргумент не является
бесконечно малым. Аналогично:
8) 
Методические указания для решения практической работы на тему
«Предел числовой последовательности и функции»
№ 1 Найдите пределы: 1.1  1.2
1.2 
1.3  1.4.
1.4.  1.5.
1.5. 
…………………………………………………………………………………………………..
Решение
1.1. 

1.2. 
1.3. 

1.4. 
1.5. 
…………………………………………………………………………………………………………………
№2 Найдите 
Решение



…………………………………………………………………………………………………………………
№ 3 Дана функция 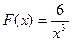 . Найдите
. Найдите 
Решение
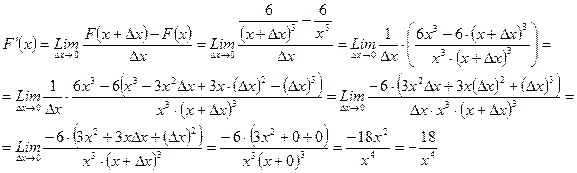
……………………………………………………………………………………………………………………..
№ 4 Исследовать функцию  н а непрерывность:
н а непрерывность:
Исследуем точку х0 = 1. Односторонние пределы в этой точке:

Пределы конечные, разные.
Следовательно, х0 = 1 является точкой разрыва 1-го рода.
………………………………………………………………………………………………






