При рассмотрении движения жидкости считают, что в потоке жидкость сплошь заполняет занимаемое ею пространство без образования пустот, т.е. движение жидкости происходит неразрывно. В этом случае справедливо уравнение неразрывности движения, выводимое на основе закона сохранения массы. Получим вначале уравнение неразрывности при установившемся движении жидкости для элементарной струйки.
Пусть имеем элементарную струйку (рис. 17). Возьмем сечение 1-1 с площадью 
искоростью движения частиц жидкости и1. Элементарный расход через сечение 1-1 [по формуле (67а), § 2.2 ]равен
.
Затем возьмем сечение 2-2 в этой же струйке с площадью сечения 
и скоростью u1. Элементарный расход через сечение 2-2 равен
.
Но по свойству элементарной струйки приток и отток жидкости через ее боковую поверхность невозможен (см. § 2.1); кроме того, в отсеке 12, который сохраняет неизменные размеры, не образуется пустот и не происходит переуплотнений; значит количества жидкости, протекающей н единицу времени через сечения 1-1 и 2-2, должны быть одинаковы, т.е. 
. Принимая во внимание, что сечения 1-1 и 2-2 приняты произвольно, можно в общем случае для элементарной струйки написать
,
или
. (69)
Это и есть уравнение неразрывности (сплошности) для элементарной струйки, которое читается так: элементарный расход жидкости 
при установившемся движении есть величина постоянная для всей элементарной струйки.
Пусть теперь имеем поток жидкости (рис. 18). Взяв в потоке два произвольных сечения 1-1 и 2-2 и представив живые сечения их состоящими из суммы элементарных струек, можно написать 
–расход жидкости в сечении 1-1; 
– расход жидкости в сечении 2-2.
Но поскольку скорости касательны к боковой поверхности потока, то в отсек между сечениями 1-1 и 2-2 через боковую поверхность движения жидкости не происходит; не изменяется и объем отсека. Следовательно, в отсек через сечение 1-1 поступает столько же жидкости, сколько за то же время выходит 
. Но так как сечения 1-1 и 2-2 взяты произвольно, то можно написать, что 
или, выражая расход жидкости в сечениях через среднюю скорость v, получим
. (69')
Это и есть уравнение неразрывности для потока жидкости, которое читается так: р асход жидкости через любое сечение потока при установившемся движении есть величина постоянная. Из уравнения (69) для двух сечений можно написать
, (70)
т.е. средние скорости потока обратно пропорциональны площадям соответствующих живых сечений.
Уравнение Д. Бернулли
Уравнение Даниила Бернулли является основным уравнением гидродинамики. Ниже разбирается это уравнение для установившегося плавно изменяющегося движения жидкости, с помощью которого решаются основные задачи гидродинамики. Введем понятия удельной энергии элементарной струйки и потока жидкости.
Удельная энергия элементарной струйки. Напомним, что удельная энергия есть энергия, отнесенная к единице силы тяжести жидкости. Пусть имеем в элементарной струйке частицу массой m, которая обладает некоторой скоростью и, находится под гидродинамическим давлением р, занимает некоторый объем V и находится от произвольной плоскости сравнения о-о на некоторой высоте z (рис. 20). Масса частицы обладает запасом удельной потенциальной энергии еп, которая складывается из удельных потенциальных энергий положения епол, и давления едав. В самом деле, масса жидкости, поднятая на высоту z, имеет запас потенциальной энергии, равный mgz, где g – ускорение свободного падения. Удельная потенциальная энергия положения равна потенциальной энергии, деленной на силу тяжести жидкости (
)
. (а)
Масса жидкости занимает некоторый объем V, находящийся под давлением р. Потенциальная энергия давления равна р V. Удельная же потенциальная энергия давления равна потенциальной энергии pV, деленной на силу тяжести данного объема gV, т. е.
. (б)
Полный запас удельной потенциальной энергии массы жидкости равен их сумме, т. е. 
и, учитывая выражения (а) и (б), напишем
. (в)
Кроме того, масса жидкости т движется со скоростью и и обладает кинетической энергией 
; но сила тяжести этой массы равна mg, и удельная кинетическая энергия струйки равна
. (г)
Складывая выражения (в) и (г), получим выражение полной удельной энергии элементарной струйки
. (71)
Здесь 
– удельная кинетическая энергия;
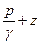– удельная потенциальная энергия давления и положения.
Полная удельная энергия потока Е складывается из удельной потенциальной энергии 
и удельной кинетической энергии Ек потока.
Для случая установившегося плавно изменяющегося движения жидкости удельная потенциальная энергия во всех точках живого сечения одинакова и равна
. (д)
Поток жидкости рассматривается как совокупность п элементарных струек, каждая из которых обладает своей удельной кинетической энергией . Эта величина различна для разных струек, образующих поток.
Определим среднее значение этой величины в сечении потока. Для этого действительные скорости элементарных струек u1, u2,..., ип заменим средней скоростью потока v;тогда среднее значение удельной кинетической энергии потока в данном сечении равно
. (е)
Здесь a – коэффициент Кориолиса, учитывающий неравномерность распределения скоростей по сечению потока (или корректив кинетической энергии).
Безразмерный коэффициент a представляет собой отношение действительной кинетической энергии потока к кинетической энергии, вычисленной по средней скорости. Если эпюра скоростей в сечении потока близка к прямоугольной, т.е. скорости в разных точках близки к средней, то коэффициент Кориолиса a близок к единице. Если же скорости в сечении значительно различаются между собой, то и коэффициент a оказывается значительно больше единицы.
Рассмотрим, например, поток глубиной Н = 6м, в сечении которого скорости распределены по треугольнику, т.е. у дна скорость равна нулю и к поверхности нарастает по закону прямой до наибольшего значения ипов = 3 м/сек. Средняя скорость v = 1,5 м/сек, а соответствующая ей кинетическая энергия
м.
Оценим кинетическую энергию потока точнее. Для этого возьмем три точки на высоте h1 = 1м; h2 = 3 м и h3 = 5 м, которые лежат посредине слоев равной высоты по 2 м каждый. Скорость в этих точках соответственно и1 = 0,5; и2 = 1,5 и и3 = 2,5 м/сек. Вычислим кинетическую энергию по этим трем скоростям
м,
что больше, чем по средней скорости.
Коэффициент Кориолиса получается
.
На основе обработки многочисленных данных, полученных на реках и каналах, установлено, что для больших открытых потоков 
. При равномерном движении в трубах и каналах практически 
.
В дальнейшем, за исключением особо оговоренных случаев, для упрощения расчетов будем принимать 
. Однако следует помнить, что в некоторых случаях при неравномерном распределении скоростей значения a могут быть значительно больше 1 (2 и более).
 |
Складывая удельную кинетическую и удельную потенциальную энергии потока, получим формулу полной удельной энергии потока
,
а учитывая выражения (е) и (д), имеем
, (72)
т.е. полная удельная энергия потока равна сумме удельной кинетической и удельной потенциальной (давления и положения) энергий потока. Напомним, что все выводы сделаны для установившегося, плавно изменяющегося движения жидкости.
Уравнение Д. Бернулли для элементарной струйки. Выделим в установившемся потоке реальной жидкости элементарную струйку (рис. 21) и определим удельную энергию жидкости в двух произвольных сечениях 1-1 и 2-2. Высоты положения центров первого и второго сечений будут соответственно z1 и z2; гидродинамическое давление и этих же точках р1 и р2 скорости течения – и1 и и2. Тогда полная удельная энергия элементарной струйки в сечении 1-1 на основании формулы (71) равна
, (ж)
а в сечении 2-2
. (з)
Практически всегда 
,так как часть полной энергии затрачивается на преодоление сил сопротивления (трения) при движении жидкости от сечения 1-1 к сечению 2-2. Обозначим эти потери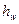 
. Тогда в соответствии с законом сохранения энергии можно написать, что 
,и, учитывая выражения (ж) и (з), получим
. (73)
Уравнение (73) и есть уравнение Д. Бернулли для элементарной струйки реальной жидкости при установившемся движении, которое устанавливает связь между скоростью движения, давлением в жидкости и положением точки в пространстве. Оно справедливо для любых двух сечений, так как сечения 1-1 и 2-2 были взяты произвольно. Уравнение (73) можно изобразить и графически (рис. 21). Если соединить уровни жидкости в пьезометрах, присоединенных к нескольким сечениям, получим некоторую линию р-р, которая называется пьезометрической линией и показывает изменение удельной потенциальной энергией по длине элементарной струйки. Если соединить точки, которые в каждом сечении вертикали изображают полную удельную энергию (а такие точки действительно можно получить, о чем см. ниже), получим некоторую линию N-N, которая называется напорной линией или линией энергии; она показывает изменение полной удельной энергии по длине струйки. Тогда расстояние по вертикали в любом сечении между горизонтальной плоскостью I - I, соответствующей начальному запасу удельной энергии в первом сечении, и напорной линией N-N дает величину потерь энергии hw на преодоление сил сопротивления на участке от первого сечения до данного сечения, а расстояние между напорной и пьезометрической линиями – удельную кинетическую энергию в данном сечении u2/2g.
Для идеальной жидкости, где отсутствуют силы трения, в уравнении (IV.7) hw= 0 и уравнение Бернулли принимает вид
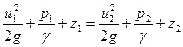. (73 /)
Но так как сечения 1-1 и 2-2 взяты произвольно, то в общем виде уравнение Бернулли для элементарной струйки идеальной жидкости записывается так:
. (73")
Уравнение Д. Бернулли для потока. Рассмотрим поток при установившемся, плавно изменяющемся движении (рис. 22). Выберем произвольно два сечения 1-1 и 2-2, по осям которых соответственно имеем z1 и z2 – вертикальные координаты оси потока над произвольной плоскостью сравнения о-о, р1 и p2 гидродинамические давления, в тех же точках v1 и v2 – средние скорости в сечениях 1-1 и 2-2.
Полную удельную энергию потока определяем по формуле (72): сечение 1-1
,
сечение 2-2
.
Очевидно 
, так как часть энергии потратится на преодоление сил сопротивления (трения). Обозначим потерю энергии на этом участке – 
. Тогда можно написать, что 
и, подставляя значения 
и 
, получим
. (74)
Уравнение (74) называется уравнением Д. Бернулли для потока жидкости и является основным уравнением гидродинамики; с его помощью получены многие расчетные формулы и решается ряд практических задач. Уравнение Бернулли устанавливает математическую связь между основными элементами движения жидкости, т. е. средней скоростью и гидродинамическим давлением.
