ТЕМА: Вимірювання ємності конденсатора, та дослідження накопичення заряду в ньому.
НАВЧАЛЬНА МЕТА: Ознайомитись з вимірюванням ємності конденсатора методом балістичного гальванометра.
ОБЛАДНАННЯ ТА ОСНАЩЕННЯ: ПЕОМ; ПЗ: Electronics Workbench.
ОСНОВНІ ТЕОРЕТИЧНІ ПЛОЖЕННЯ
Якщо двом ізольованим один від одного провідникам надати заряди q1 і q2, то між ними виникає деяка різниця потенціалів 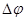 , залежна від величин зарядів і геометрії провідників. Різниця потенціалів
, залежна від величин зарядів і геометрії провідників. Різниця потенціалів 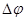 між двома точками в електричному полі часто називають напругою і означають буквою U. Найбільший практичний інтерес представляє випадок, коли заряди провідників однакові по модулю і протилежні по знаку: q1 = - q2 = q. В цьому випадку можна ввести поняття електричної ємності.
між двома точками в електричному полі часто називають напругою і означають буквою U. Найбільший практичний інтерес представляє випадок, коли заряди провідників однакові по модулю і протилежні по знаку: q1 = - q2 = q. В цьому випадку можна ввести поняття електричної ємності.
Електроємністю системи з двох провідників називається фізична величина, визначувана як відношення заряду q одного з провідників до різниці потенціалів 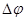 між ними:
між ними:
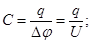 (1)
(1)
У системі СІ одиниця електроємності називається фарад (Ф):
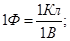 (2)
(2)
Величина електроємності залежить від форми і розмірів провідників і від властивостей діелектрика, що розділяє провідники. Існують такі конфігурації провідників, при яких електричне поле виявляється зосередженим (локалізованим) лише в деякій області простору. Такі системи називаються конденсаторами, а провідники, що складають конденсатор, - обкладаннями.
Величина електроємності залежить від форми і розмірів провідників і від властивостей діелектрика, що розділяє провідники. Існують такі конфігурації провідників, при яких електричне поле виявляється зосередженим (локалізованим) лише в деякій області простору. Такі системи називаються конденсаторами, а провідники, що становлять конденсатор, - обкладаннями.
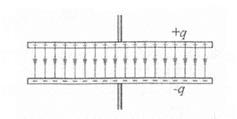
Простий конденсатор - система з двох плоских пластин, розташованих паралельно один одному на малій в порівнянні з розмірами пластин відстані і розділених шаром діелектрика. Такий конденсатор називається плоским. Електричне поле плоского конденсатора в основному локалізоване між пластинами (мал. 1); проте, поблизу країв пластин і в навколишньому просторі також виникає порівняно слабке електричне поле, яке називають полем розсіяння. У цілому ряду задач приблизно можна нехтувати полем розсіяння і вважати, що електричне поле плоского конденсатора цілком зосереджене між його обкладаннями (мал. 2). Але в інших задачах знехтуванням полем розсіяння може привести до грубих помилок, оскільки при цьому порушується потенційний характер електричного поля.
 |
Малюнок 1 - Поле плоского конденсатора.
|
Малюнок 2 - Представлення поля плоского конденсатора, що ідеалізується.
Таке поле не має властивості потенційності.
Кожна із заряджених пластин плоского конденсатора створює поблизу поверхні електричне поле, модуль напруженості якого виражається співвідношенням:
 (3)
(3)
Згідно з принципом суперпозиції, напруженість поля, що створюється обома пластинами, дорівнює сумі напруженості полів кожної з пластин:
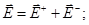 (4)
(4)
Усередині конденсатора вектора паралельні; тому модуль напруженості сумарного поля рівний
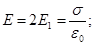 (5)
(5)
Поза пластинами вектора спрямовані в різні боки, і тому Е = 0. Поверхнева щільність 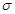 заряду пластин рівна q/S, де q - заряд, а S - площа кожної пластини. Різниця потенціалів
заряду пластин рівна q/S, де q - заряд, а S - площа кожної пластини. Різниця потенціалів 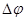 між пластинами в однорідному електричному полі рівна Еd, де d - відстань між пластинами. З цих співвідношень можна отримати формулу для електроємності плоского конденсатора:
між пластинами в однорідному електричному полі рівна Еd, де d - відстань між пластинами. З цих співвідношень можна отримати формулу для електроємності плоского конденсатора:
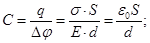 (6)
(6)
Таким чином, електроємність плоского конденсатора прямо пропорційна площі пластин і назад пропорційна відстані між ними. Якщо простір між обкладаннями заповнений діелектриком, електроємність конденсатора збільшується в є раз:
 (7)
(7)
Прикладами конденсаторів з іншою конфігурацією обкладань можуть служити сферичний і циліндричний конденсатори. Сферичний конденсатор - це система з двох концентричних сфер радіусів R1 і R2. Циліндричний конденсатор - система з двох співісних циліндрів радіусів R1 і R2 і довжини L. Ємності цих конденсаторів, заповнених діелектриком з діелектричною проникністю є, виражаються формулами:
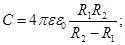 (8)
(8)
Вимірювання ємності конденсатора методом балістичного гальванометра, проводять за допомогою еталонного конденсатора(конденсатора ємність якого відома).
Якщо еталонний і досліджуваний конденсатор зарядити до однакової різниці потенціалів, то з формули 1 маємо:
 (9)
(9)
де: С - ємність еталонного конденсатора, Сх - ємність досліджуваного конденсатора, q1, qx - відповідно їх заряди.
З формули 9:
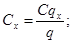 (10)
(10)
Заряд конденсатора можна виміряти за допомогою міліамперметра, розрядивши конденсатор на міліамперметр 2 мал. 3. Показання міліамперметра тим більше, чим більший заряд проходить через міліамперметр:
q=kn (11)
де: k - стала яка залежить від міліамперметра та кола, n - максимальне значення струму що проходить через міліамперметр.
З формул 10-11 отримуємо остаточну формулу для розрахунку.
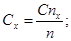 (12)
(12)
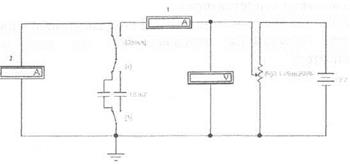 Малюнок З - Схема дослідження
Малюнок З - Схема дослідження
|
ХІД РОБОТИ
1 Запустити Electronics Workbench, відкрити схему для дослідження обравши меню File\Open, та обрати «Конденсатор.ewb».
2 Вивчити схему, розібратися з керуванням схеми, натиснувши на клавішу «Space» перемкнути ключ переключання конденсаторів з заряду на розряд, натиснувши клавішу «1» перемкнути ключ зміни конденсатора.
3 Включити схему в правому верхньому кутку екрану натиснувши відповідну кнопку.
4 За допомогою ключа «1» обрати конденсатор відомої ємності (С=10мкФ).
5 За допомогою ключа «Space» включити заряджання конденсатора.
6 Після закінчення заряджання конденсатора (покази амперметра 1 рівні 0, мал. 3) ключем «Space» перемкнути конденсатор на розряд, та записати максимальний показ амперметра 2 до таблиці 1.
7 Повторити пункти 5-6 двічі.
8 За допомогою ключа «1» обрати конденсатор невідомої ємності (Сх).
9 Повторити для конденсатора Сх пункти 5-6 тричі.
10 Обчислити ємність невідомого конденсатора за формулою 12.
11 Розрахувати абсолютну похибку ДСХ та відносну - є за формулами:
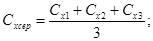
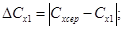
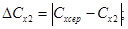
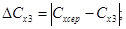
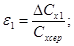
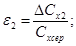
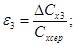
12. Дані обчислень занести до таблиці 1.
13. Дати відповідь на контрольні запитання.
Таблиця 1
| № досліду | Ємність C, мкФ | Сила струму n | Сила струму nх | Ємність Сх, мкФ | ΔСx | ε |
ЗМІСТ ЗВІТУ
1 Мета роботи
2 Обладнання
3 Таблиці з дослідженнями та розрахунками
4 Розрахунки
5 Висновки
КОНТРОЛЬНІ ЗАПИТАННЯ ДО ЗАХИСТУ:
1 Що називають ємністю конденсатора?
2 Якими одиницями вимірюється ємність конденсатора?
3 Що таке заряд конденсатора?
4 Чому під час вимірювання ємності конденсатора потрібно підтримувати таку напругу заряджання конденсаторів, до якої заряджали еталонний конденсатор?






