Цель экономико-статистического анализа производительности труда – выявить причины (факторы), повлиявшие на формирование среднего уровня, характер и темпы изменения производительности труда, для подготовки, обоснования и принятия экономических решений. Существуют несколько методов экономико-статистического анализа производительности труда, каждый из которых обладает самостоятельным значением, условиями и сферой применения. Рассмотрим каждый из них в отдельности.
Для анализа динамики производительности труда может применяться разновидность индексного метода – метод цепных подстановок. Этот метод используют для факторного анализа производительности труда. Сущность его состоит в том, что производительность труда выражают в виде произведения факторов, влияющих на нее, и находят влияние каждого фактора на изменение производительности труда.
Если уровень производительности труда зависит от трех факторов – а,b,с, то 
.
Для характеристики влияния каждого фактора на изменение производительности труда вычисляют частные (факторные) индексы. При этом возможны две системы вычисления:
– по схеме обособленных частных индексов;
– по схеме взаимосвязанных частных индексов.
В первом случае (т.е. по схеме обособленных частных индексов) исходят из предположения, что изменяется только данный фактор, а значения всех остальных сохраняются на базисном уровне, то есть расчеты производятся по формулам:
– влияние фактора а; (15)
– влияние фактора b; (16)
– влияние фактора с. (17)
Или в абсолютном выражении:
– влияние фактора а; (18)
– влияние фактора b; (19)
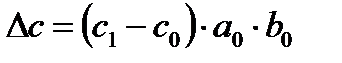– влияние фактора с; (20)
Сумма этих изменений 
не совпадает с общим изменением производительности труда. Это объясняется тем, что влияние каждого фактора было рассмотрено изолированно от влияния других факторов. Реально факторы влияют на изменение производительности труда совместно. Эту взаимосвязь факторов выявляют путем построения системы взаимосвязанных частных индексов.
Исследуя влияние факторов в их взаимосвязи, надо расположить сами факторы в определенной последовательности, полагая при этом, что влияние взаимодействия всех факторов будет отражено в основном ведущем факторе.
Изучая на предприятии динамику или выполнение плана производительности труда можно с помощью индексного метода определить влияние изменения средней часовой производительности труда, использования рабочего времени внутри дня и использования рабочих по числу дней работы на общую динамику
Взаимосвязь факторов можно выявить путем построения по схеме взаимосвязанных частных индексов.
При построении таких индексов следует исходить из следующего положения: индекс качественного фактора надо строить применительно к объемному фактору на уровне отчетного периода, а индекс объемного фактора при сохранении качественного фактора на уровне базисного периода. Причем при выделении трех и более факторов необходимо исходить из попарного разложения факторов.
Например, можно начать с двух факторов – средней часовой выработки (а) и среднего числа часов работы (b–c). Так как первый фактор качественный, то его влияние надо изучать при величине второго фактора на уровне отчетного периода, то есть:
. (21)
Но число часов работы одного рабочего состоит из двух факторов, причем по отношению к этому произведению b – средняя продолжительность рабочего дня – качественный, а фактор с – среднее число дней работы одного рабочего – объемный. Отсюда индекс фактора b:
, (22)
а индекс фактора с:
. (23)
При такого рода построениях важно, чтобы каждый укрупненный фактор представлял собой экономически осмысленную величину. Размер абсолютного влияния каждого фактора рассчитывается следующим образом:
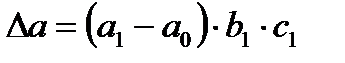– влияние фактора a, (24)
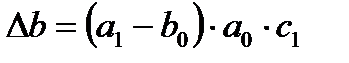– влияние фактора b, (25)
– влияние фактора c. (26)
Обособленное изучение факторов и построение системы взаимосвязанных частных индексов дополняют друг друга и дают возможность анализировать влияние ряда факторов на выполнение плана и динамику производительности труда. Число этих факторов может быть значительно увеличено по сравнению с рассмотренным выше примером, и тем самым анализ может быть углублен.
Индексный метод анализа производительности труда можно применять только в тех случаях, когда установлено наличие функциональной зависимости между производительностью труда и ее факторами. Для нахождения связи между факторами и результативным признаком (производительностью труда) применяют метод статистических группировок, в частности аналитические группировки. Суть их состоит в том, что все элементы изучаемой совокупности разбиваются на группы по степени силы действия изучаемого фактора. В пределах каждой группы влияние изучаемого фактора можно считать одинаковым или почти одинаковым для всех элементов совокупности, попавших в данную группу.
Дисперсионный анализ дает возможность установить влияние группировочного признака и влияние случайных величин на результативный признак. При этом общая дисперсия результативного признака 
расчленяется на факторную 
и остаточную (или случайную)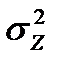 
; факторную дисперсию сравнивают со случайной с учетом степеней свободы. Число степеней свободы: для общей дисперсии – число значений варьирующего результативного признака без одного (n–1), для факторной дисперсии – число групп без одной (I–1), для случайной дисперсии – число значений результативного признака без числа групп (n–1). Обозначив сумму квадратов отклонений через D2, получим дисперсию на одну степень свободы:
– общую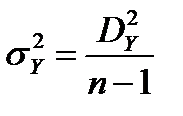 
; (24)
– факторную 
; (25)
– случайную 
. (26)
Общая дисперсия определяется по формуле 
. (27)
Далее вся совокупность делится на однородные группы. Для каждой группы рассчитывают среднюю и дисперсию. В результате получают внутригрупповую и межгрупповую дисперсии. Общая дисперсия показывает влияние всех условий (факторов) на вариацию признака Внутригрупповая (случайная) дисперсия показывает влияние случайных, не учитываемых условий (факторов) на вариацию признака, то есть зависит от группировочного признака. Она представляет собой среднюю из частных (групповых) дисперсий (
) и рассчитывается по формуле:
, (28)
а частные (групповые) дисперсии рассчитываются следующим образом:
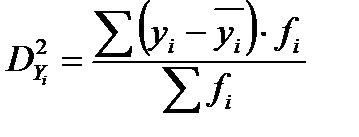. (29)
Межгрупповая дисперсия характеризует вариацию признака под влиянием определяющих условий, связанных с группировочным признаком. Она представляет собой средний квадрат отклонения групповых средних от общей средней и вычисляется по формуле:
. (30)
Оценка достоверности влияния факторного признака на результативный производится с помощью рассчитанного значения F-критерия (критерия Фишера). Критерий Фишера есть отношение факторной и случайной дисперсий, рассчитанных на одну степень свободы:
. (31)
Величина рассчитанного критерия сравнивается с его табличным значением, установленным для 1- и 5-процентного уровня значимости, если значение FФАКТ < FТАБЛ.
Регрессионный анализ позволяет определить меру интенсивности направленного влияния факторов при формировании уровня производительности труда в конкретных условиях места и времени. Вначале устанавливается тип и вид функции уравнения связи. Конкретное выражение формы связи зависит от характера объективно существующей зависимости исследуемых явлений, т.е. определяется материальной природой объекта.
Количественная определенность параметров уравнения связи устанавливается чаще всего по методу наименьших квадратов. При этом находятся такие численные значения коэффициентов при факторных признаках в уравнении регрессии, при которых сумма квадратов отклонений эмпирических значений результативного показателя от аналогичных им величин, рассчитанных по теоретическому уравнению регрессии, давала бы минимальную величину.
Корреляционный анализ дает возможность измерить взаимосвязь (тесноту связи) факторного и результативного признаков. Для этого предварительно устанавливается для каждой группы центр интервала по размеру производительности труда, а затем рассчитывается коэффициент корреляции по формуле:
, (32)
где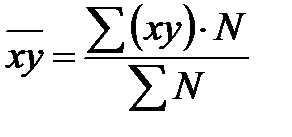 
; 
; 
;
;
;
X – группировочный (факторный) признак;
Y – результативный признак;
N – численность совокупности;
M – математическое ожидание;
h – среднее квадратичное отклонение.
Вычисление коэффициента корреляции является наиболее точным, если оно проводится по всему массиву не сгруппированных первичных данных.
Расчетная часть
Краткая характеристика предприятия
Объект исследования. Лениногорское управление тампонажных работ.
Юридический адрес. 423250, Татарстан г. Лениногорск, ул. Чайковкого, д.29 д.
Лениногорское управление тампонажных работ является одним из подразделений ОАО «Татнефть».
Лениногорское управление тампонажных работ создано в целях удовлетворения общественных потребностей в товарах и услугах и извлечения прибыли и в своей деятельности руководствуется уставом, законодательством Российской Федерации для исполнения актами исполнительных органов власти.
Основным видом деятельности компании является разработка и геодезическое изучение нефтяных месторождений, расположенных на территории Республики Татарстан.
Предприятие также занимается сервисным обслуживанием объектов предприятий ОАО «Татнефть»; эксплуатацией производств и объектов нефтяной и газовой промышленности; а также производит техобслуживание и ремонт оборудования для нефтяной и газовой промышленности по договорам с предприятиями ОАО «Татнефть».
Методика расчета
Для расчета показателей динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисляемые при этом показатели называются базисными.
Для расчета показателей динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким способом показатели динамики называются цепными.
Важнейшим статистическим показателем динамики является абсолютный прирост, который определяется в разностном сопоставлении двух уровней ряда динамики в единицах измерения исходной информации.
Абсолютный прирост
цепной прирост: ∆y ц = y i - y i-1
базисный прирост: ∆y б = y i - y 1
Темпы прироста характеризуют абсолютный прирост в относительных величинах. Исчисленный в процентах темп прироста показывает, на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения.
Темп прироста
цепной темп прироста: T прцi = ∆yi / y i-1
базисный темп прироста: T пpб = ∆yбi / y 1
Распространенным статистическим показателем динамики является темп роста. Он характеризует отношение двух уровней ряда и может выражаться в виде коэффициента или в процентах.
Темп роста
цепной темп роста: T pцi = y i / y i-1
базисный темп роста: T pб = yбi / y 1
Абсолютное значение 1% прироста
цепной: 1% цi = y i-1 / 100%
базисный: 1% б = yб / 100%
Темп наращения
Важным статистическим показателем динамики социально-экономических процессов является темп наращивания, который в условиях интенсификации экономики измеряет наращивание во времени экономического потенциала
T н = ∆yцi / y 1
| Цепные показатели ряда динамики Период | выполненный объем тампонажных работ заказчика | Абсолютный прирост | Темп прироста, % | Темпы роста, % | Абсолютное содержание 1% прироста | Темп наращения, % |
| 3643.23 | ||||||
| 5.26 | 105.26 | 3643.23 | 5.26 | |||
| 13.64 | 113.64 | 3834.98 | 14.35 | |||
| 7.53 | 107.53 | 4357.93 | ||||
| 11.11 | 111.11 | 4685.95 | 14.29 | |||
| 8.7 | 108.7 | 5206.61 | 12.43 | |||
выполненный объем тампонажных работ заказчика в 2010 составил 565936
Отобразим динамику выполненных работ на графике 1
В 2010 по сравнению с 2009 выполненный объем тампонажных работ заказчика увеличилось на 45275 или на 8.7%
В 2010 выполненный объем тампонажных работ заказчика составила 565936 и за прошедший период увеличилось на 45275, или на 8.7%
Максимальный прирост наблюдается в 2007 (52295)
Минимальный прирост зафиксирован в 2006 (19175)
Темп наращения показывает, что тенденция ряда возрастающая, что свидетельствует об ускорении выполненный объем тампонажных работ заказчика
| Базисные показатели ряда динамики Период | выполненный объем тампонажных работ заказчика | Абсолютный прирост | Темп прироста, % | Темпы роста, % |
| 5.26 | 105.26 | |||
| 19.62 | 119.62 | |||
| 28.62 | 128.62 | |||
| 42.91 | 142.91 | |||
| 55.34 | 155.34 |
выполненный объем тампонажных работ заказчика в 2010 составил 565936
В 2010 по сравнению с 2005 выполненный объем тампонажных работ заказчика увеличилось на 201613 или на 55.34%
В 2010 выполненный объем тампонажных работ заказчика составила 565936 и за прошедший период увеличилось на 201613, или на 55.34%
Максимальный прирост наблюдается в 2010 (201613)
Минимальный прирост зафиксирован в 2006 (19175)
Расчет средних характеристик рядов
Средний уровень ряда y динамики характеризует типическую величину абсолютных уровней
Средний уровень ряда динамики
Среднее значение выполненный объем тампонажных работ заказчика с 2005 по 2010 составило 456467.67
Средний темп роста
В среднем за весь период с 2005 по 2010 рост выполненный объем тампонажных работ заказчика составил 1.0921
Средний темп прироста
В среднем каждый период выполненный объем тампонажных работ заказчика изменялось 9.21%
Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики.
Средний абсолютный прирост
В среднем за весь период выполненный объем тампонажных работ заказчика увеличивалось на 40322.6 за каждый период
Расчет за 12 месяцев 2010 года
| Цепные показатели ряда динамикиПериод | объем выполненных тампонажных работ | Абсолютный прирост | Темп прироста, % | Темпы роста, % | Абсолютное содержание 1% прироста | Темп наращения, % |
| 1.01 | 405.35 | |||||
| 1.02 | 18.5 | 118.5 | 405.35 | 18.5 | ||
| 1.03 | -2227 | -4.64 | 95.36 | 480.32 | -5.49 | |
| 1.04 | 4.58 | 104.58 | 458.05 | 5.17 | ||
| 1.05 | 6.56 | 106.56 | 479.02 | 7.75 | ||
| 1.06 | -446 | -0.87 | 99.13 | 510.44 | -1.1 | |
| 1.07 | 14.83 | 114.83 | 505.98 | 18.51 | ||
| 1.08 | -7699 | -13.25 | 86.75 | 581.01 | -18.99 | |
| 1.09 | 0.4 | 100.4 | 504.02 | 0.5 | ||
| 1.10 | -12669 | -25.04 | 74.96 | 506.03 | -31.25 | |
| 1.11 | -6168 | -16.26 | 83.74 | 379.34 | -15.22 | |
| 1.12 | 3.68 | 103.68 | 317.66 | 2.89 | ||
объем выполненных тампонажных работ в 1.12 составил 32936
Динамика выполненных работ изображена на графике 2
В 1.12 по сравнению с 1.11 объем выполненных тампонажных работ увеличилось на 1170 или на 3.68%
В 1.12 объем выполненных тампонажных работ составила 32936 и за прошедший период увеличилось на 1170, или на 3.68%
Максимальный прирост наблюдается в 1.07 (7503)
Минимальный прирост зафиксирован в 1.10 (-12669)
Темп наращения показывает, что тенденция ряда возрастающая, что свидетельствует об ускорении объем выполненных тампонажных работ
| Базисные показатели ряда динамикиПериод | объем выполненных тампонажных работ | Абсолютный прирост | Темп прироста, % | Темпы роста, % |
| 1.01 | ||||
| 1.02 | 18.5 | 118.5 | ||
| 1.03 | ||||
| 1.04 | 18.17 | 118.17 | ||
| 1.05 | 25.93 | 125.93 | ||
| 1.06 | 24.83 | 124.83 | ||
| 1.07 | 43.34 | 143.34 | ||
| 1.08 | 24.34 | 124.34 | ||
| 1.09 | 24.84 | 124.84 | ||
| 1.10 | -2601 | -6.42 | 93.58 | |
| 1.11 | -8769 | -21.63 | 78.37 | |
| 1.12 | -7599 | -18.75 | 81.25 |
объем выполненных тампонажных работ в 1.12 составил 32936
В 1.12 по сравнению с 1.01 объем выполненных тампонажных работ уменьшилось на 7599 или на 18.75%
В 1.12 объем выполненных тампонажных работ составила 32936 и за прошедший период увеличилось на 7599, или на 18.75%
Максимальный прирост наблюдается в 1.07 (17566)
Минимальный прирост зафиксирован в 1.11 (-8769)
Расчет средних характеристик рядов
Средний уровень ряда y динамики характеризует типическую величину абсолютных уровней
Средний уровень ряда динамики
Среднее значение объем выполненных тампонажных работ с 1.01 по 1.12 составило 45471.5
Средний темп роста
В среднем за весь период с 1.01 по 1.12 рост объем выполненных тампонажных работ составил 0.9813
Средний темп прироста
В среднем каждый период объем выполненных тампонажных работ изменялось -1.87%
Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики.
Средний абсолютный прирост
В среднем за весь период объем выполненных тампонажных работ уменьшалось на 690.82 за каждый период
Рассчитанные значения индекса сезонности сравниваются со значением 100 %. Если индекс сезонности превышает 100 % — это свидетельствует о влиянии сезонного фактора в сторону увеличения уровней динамического ряда.
Если индекс сезонности меньше 100 % — то сезонный фактор вызывает снижение уровней динамического ряда.
Определим наличие сезонных колебаний для динамического ряда.
| Период | ∆сез | ∆отн,% | Iсез, % | |||
| Январь | 38771.5 | -4904.96 | -11.23 | 88.77 | ||
| Февраль | 45942.5 | 2266.04 | 5.19 | 105.19 | ||
| Март | 43812.5 | 136.04 | 0.3115 | 100.31 | ||
| Апрель | 2141.54 | 4.9 | 104.9 | |||
| Май | 48823.5 | 5147.04 | 11.78 | 111.78 | ||
| Июнь | 50593.5 | 6917.04 | 15.84 | 115.84 | ||
| Июль | 55573.5 | 11897.04 | 27.24 | 127.24 | ||
| Август | 48209.5 | 4533.04 | 10.38 | 110.38 | ||
| Сентябрь | 48401.5 | 4725.04 | 10.82 | 110.82 | ||
| Октябрь | -7392.46 | -16.93 | 83.07 | |||
| Ноябрь | -13292.46 | -30.43 | 69.57 | |||
| Декабрь | 31503.5 | -12172.96 | -27.87 | 72.13 | ||
| 43676.46 |
Линейное уравнение тренда имеет вид y = bt + a
1. Находим параметры уравнения методом наименьших квадратов.
Система уравнений МНК:
a0n + a1∑t = ∑y
a0∑t + a1∑t2 = ∑y•t
Для наших данных система уравнений имеет вид:
12a0 + 78a1 = 545658
78a0 + 650a1 = 3413778
Из первого уравнения выражаем а0 и подставим во второе уравнение
Получаем a0 = -930.06, a1 = 51516.91
Уравнение тренда:
y = -930.06 t + 51516.91
Эмпирические коэффициенты тренда a и b являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
Коэффициент тренда b = -930.06 показывает среднее изменение результативного показателя (в единицах измерения у) с изменением периода времени t на единицу его измерения. В данном примере с увеличением t на 1 единицу, y изменится в среднем на -930.06.
Ошибка аппроксимации.
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.
Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения тренда к исходным данным.
Поскольку ошибка больше 7%, то данное уравнение не желательно использовать в качестве тренда.
Однофакторный дисперсионный анализ.
Средние значения
Дисперсия
Среднеквадратическое отклонение
Коэффициент эластичности.
Коэффициент эластичности представляет собой показатель силы связи фактора t с результатом у, показывающий, на сколько процентов изменится значение у при изменении значения фактора на 1%.
Коэффициент эластичности меньше 1. Следовательно, при изменении t на 1%, Y изменится менее чем на 1%. Другими словами - влияние t на Y не существенно.
Эмпирическое корреляционное отношение.
Эмпирическое корреляционное отношение вычисляется для всех форм связи и служит для измерение тесноты зависимости. Изменяется в пределах [0;1].
где
В отличие от линейного коэффициента корреляции он характеризует тесноту нелинейной связи и не характеризует ее направление. Изменяется в пределах [0;1].
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < η < 0.3: слабая;
0.3 < η < 0.5: умеренная;
0.5 < η < 0.7: заметная;
0.7 < η < 0.9: высокая;
0.9 < η < 1: весьма высокая;
Полученная величина свидетельствует о том, что изменение временного периода t умеренно влияет на y.
Коэффициент детерминации.
т.е. в 17.52% случаев влияет на изменение данных. Другими словами - точность подбора уравнения тренда - низкая.
Заключение
Общий уровень производительности определяют два типа факторов:
1) краткосрочные -- объективные (например, изменение номенклатуры сырья и видов энергии в связи с авариями, цикличные колебания качества сырья); субъективные (например, колебание уровня трудоспособности в течение дня, недели, года);
2) долгосрочные (например, цены на материалы, энергию, качество оборудования).
Как видно, производительность связана с количеством (количеством часов, трудозатратами) и качеством труда (особенностями технологии, объемом капитальных вложений, качеством персонала).
Список использованной литературы
1. Елисеева И.И., Юзбашева М.М. Общая теория статистики, – М.,1995 г.
2. Статистика промышленности, под ред. Адамова В.Е., – М., 1987 г.
3. Савицкая Г. В. Анализ хозяйственной деятельности предприятия. – М.: Инфра‑М, 2001
4. Шеремет А.Д., Сайфулин Р.С. Методика финансового анализа – М.: ИНФРА‑М, 1999.
5. Анализ трудовых показателей: Учеб. Пособие для вузов / А.В. Никитин, Н.А. Кольцов, И.А. Самарина и др.; Под ред. П.Ф. Петроченко. – М.: Экономика, 1989.
