Показатели анализа ряда динамики. Средние показатели ряда динамики.

При изучении динамики общественных ''явлений возникает проблема описания интенсивности изменения и расчета средних показателей динамики. Анализ интенсивности изменения во времени осуществляет­ся с помощью показателей, получаемых в результате сравнения уровней, к таким показателям относятся: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процен­та прироста. Система средних показателей включает средний уровень ря­да, средний абсолютный прирост, средний темп роста, средний темп прироста. Показатели анализа динамики могут вычисляться на постоянной и переменных базах сравнения. При этом принято называть сравниваемый уровень отчетным, а уровень, с которым производится сравнение, — базисным. Для расчета показателей анализа динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же ба­зисным уровнем. В качестве базисного выбирается либо началь­ный уровень в ряду динамики, либо уровень, с которого начи­нается какой-то новый этап развития явления. Исчисляемые при этом показатели называются базисными. Для расчета показателей анализа динамики на переменной базе каждый последующий уровень ряда сравнивается с преды­дущим. Вычисленные таким образом показатели анализа дина­мики называются цепными.

Важнейшим статистическим показателем анализа динамики яв­ляется абсолютный прирост (сокращение), т.е. абсолютное изменение, характеризующее увеличение или уменьшение уровня ряда за оп­ределенный промежуток времени. Абсолютный прирост с пере­менной базой называют скоростью роста.

Абсолютный прирост (цепной) -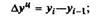

Абсолютный прирост (базисный)-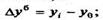

где Уi — уровень сравниваемого периода; Уi-1— уровень предшествующего периода; У0 — уровень базисного периода.

Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, т. е. общему приросту за весь промежуток вре­мени (∑∆y^Ц=∆y^Б). Для оценки интенсивности, т. е. относительного изменения уровня динамического ряда за какой-либо период времени ис­числяют темпы роста (снижения).

Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному.

Показатель интенсивности изменения уровня ряда, выра­женный в долях единицы, называется коэффициентом роста, а в процентах — темпом роста. Эти показатели интенсивности из­менения отличаются только единицами измерения.

Коэффициент роста (снижения ) показывает, во сколько раз сравниваемый уровень больше уровня, с которым произ­водится сравнение (если этот коэффициент больше единицы) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). Темп роста всегда представляет собой положительное число.

Коэффициент роста:(цепной)

Коэффициент роста: (базисный)

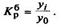
Темп роста (цепной):

Темп роста (базисный):

Итак, Т_Р =К_Р *100

Между цепными и базисными коэффициентами роста суще­ствует взаимосвязь (если базисные коэффициенты исчислены по отношению к начальному уровню ряда динамики): произведе­ние последовательных цепных коэффициентов роста равно базис­ному коэффициенту роста за весь период (П.К£ = К%), а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.

Относительную оценку скорости измерения уровня ряда.в еди­ницу времени дают показатели темпа прироста (сокращения).

Темп прироста (сокращения) показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения, и вычисляется как отношение абсолютного при­роста к абсолютному уровню, принятому за базу сравнения. Темп прироста может быть положительным» отрицательным или равным нулю, выражается он в процентах и долях единицы (коэффициенты прироста).

Темп прироста (цепной):

Темп прироста (базисный):

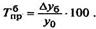
Темп прироста (сокращения) можно получить и из темпа роста, выраженного в процентах, если из него вычесть 100%. Коэффициент прироста получается вычитанием единицы из ко­эффициента роста:

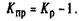
При анализе динамики развития следует также знать, какие абсолютные значения скрываются за темпами роста и прироста. Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывает, что при снижении (замедле­нии) темпов прироста абсолютный прирост не всегда уменьша­ется, в отдельных случаях он может возрастать. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением (содержанием) одного процента прироста и рассчитывают как отношение абсолютного прироста к темпу прироста за тот же период времени, %:

Абсолютное значение одного процента прироста равно сотой части предыдущего (или базисного) уровня. Оно показывает, какое абсолютное значение скрывается за относительным пока­зателем — одним процентом прироста.В тех случаях, когда сравнение производится с отдалением периода времени, принятого за базу сравнения, рассчитывают так называемые пункты роста, которые представляют собой разность базисных темпов роста, %, двух смежных периодов.В отличие от темпов прироста, которые нельзя ни суммиро­вать, ни перемножать, пункты роста можно суммировать, в ре­зультате получаем темп прироста соответствующего периода по сравнению с базисным.

Для обобщающей характеристики динамики исследуемого явления определяют средние показатели: средние уровни ряда и средние показатели изменения уровней ряда.

СРЕДНИЕ ПОКАЗАТЕЛИ РЯДА ДИНАМИКИ характеризует обобщённую вели­чину абсолютных уровней. Он рассчитывается по средней хро­нологической, т. е. по средней исчисленной из значений, изме­няющихся во времени.

Ряд динамики (или динамический ряд) представляет собой ряд расположенных в хронологической последовательности чи­словых значений статистического показателя, характ-их изменение общественных явлений во времени. В каждом ряду динамики имеются два основных элемента: время t и конкретное значение показателя (уровень ряда). Уровни ряда — это показатели, числовые значения которых составляют динамический ряд. Время — это моменты или перио­ды, к которым относятся уровни. Построение и анализ рядов динамики позволяют выявить и измерить закономерности развития общественных явлений во времени. Эти закономерности не проявляются четко на каждом конкретном уровне, а лишь в тенденции, в достаточно дли­тельной динамике. На основную закономерность динамики на­кладываются другие, прежде всего случайные, иногда сезонные влияния. Выявление основной тенденции в изменении уров­ней, именуемой трендом, является одной из главных задач ана­лиза рядов динамики. По времени, отраженному в динамических рядах, они разде­ляются на моментные и интервальные. Моментным рядом динамики называется такой ряд, уровни которого характери

Методы расчета среднего уровня интервального и моментного рядов динамики различны. Для интервальных рядов динамики из абсолютныхуровней средний уровень за период времени определяется по формуле средней арифметической: • при равных интервалах применяется средняя арифметиче­ская простая:

где у - абсолютные уровни ряда; n —число уровней ряда.

• при неравных интервалах — средняя арифметическая взве­шенная:

где У 1..... Уn — уровни ряда динамики, сохраняющиеся без изме­нения в течение промежутка времени t;

t1....tn — веса, длительность интервалов времени (дней, ме­сяцев) между смежными датами.

Средний уровень моментных рядов с неравностоящими уровнями определяется по формуле средней хронологической взвешенной:

где уi, уn - уровни рядов динамики; t — интервал времени между смежными уровнями.

Использование в расчетах формулы (7.10) рассмотрим на следую­щем примере.

Обобщающий показатель скорости изменения уровней во времени — средний абсолютный прирост (убыль ), представляющий собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. По цепным данным об абсолютных приростах за ряд лет можно рассчитать средний абсолютный при­рост как среднюю арифметическую простую:

где п - число цепных абсолютных приростов (∆у ^Ц) в изучаемом периоде. Средний абсолютный прирост определим через накопленный (базисный) абсолютный прирост (Ау,⁶). Для случая равных ин­тервалов применим следующую формулу:

где m - число уровней ряда динамики в изучаемом периоде, •' включая базисный. Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит средний темп роста (снижения), показывающий, во сколько раз в среднем за едини­цу времени изменяется уровень ряда динамики.

Средний темп роста (снижения) — обобщенная характеристика индивидуальных темпов роста ряда динамики. В качестве основы и критерия правильности исчисления среднего темпа роста (сни­жения) применяется определяющий показатель — произведение цепных темпов роста, равное темпу роста за весь рассматривае­мый период. Следовательно, если значение признака образуется как произведение отдельных вариантов, то согласно общему пра­вилу нужно применять среднюю геометрическую.

Поскольку средний темп роста представляет собой средний коэффициент роста, выраженный в процентах (Г = К 100), то для равностоящих рядов динамики расчеты по средней геомет­рической сводятся к исчислению средних коэффициентов роста I из цепных коэффициентов роста (по щепному способу»):

где n — число цепных коэффициентов роста;

Если известны уровни динамического ряда, то расчет сред­него коэффициента роста упрощается. Так как произведение цепных коэффициентов роста равно базисному, то в подкорен­ное выражение подставляется базисный коэффициент роста. Ба­зисный коэффициент, как известно, получается непосредственно как частное от деления уровня последнего периода у„ на уровень базисного периода у₀. Тогда формула для расчета среднего коэффициента роста для равностоящих рядов динамики (по «базисному способу»):

Средние темпы прироста (сокращения) рассчитываются на основе средних темпов роста, вычитанием из последних 100 %. Соответственно при исчислении средних коэффициентов прирос­та из значений коэффициентов роста вычитается единица:

где Тпр — средний темп прироста, Кпр_пр — средний коэффициент прироста

Если уровни ряда динамики снижаются, то средний темп роста будет меньше 100%, а средний темп прироста — отрица­тельной величиной. Отрицательный темп прироста Т_пр пред­ставляет собой средний темп сокращения и характеризует сред­нюю относительную скорость снижения уровня.

Сравнительные характеристики направления и интенсивно­сти роста одновременно развивающихся во времени явлений определяются приведением рядов динамики к общему (единому) р основанию и расчетом коэффициентов опережения (отставания).

Ряды динамики (в которых возникают, например, про­блемы сопоставимости цен сравниваемых стран, методики рас­чета сравниваемых показателей и т.п.) обычно приводят к одно­му основанию, если они не могут быть решены другими метода-f ми. По исходным уровням нескольких рядов динамики определяют относительные величины — базисные темпы роста или прироста. Принятый при этом за базу сравнения период време­ни (дата) выступает в качестве постоянной базы расчетов тем­пов роста для каждого из изучаемых рядов динамики. В зависи­мости от целей исследования базой может быть начальный, средний или другой уровень ряда.

Сравнение интенсивности изменений уровней рядов во вре­мени возможно с помощью коэффициентов опережении (отставания) представляющих собой отношение базисных темпов роста (или при­роста) двух рядов динамики за одинаковые отрезки времени:

где Т’р, Т'пр, Т’’р, Т’’пр ~ базисные темпы роста и прироста первого и второго рядов динамики (соответственно).

Коэффициенты опережения (отставания ) могут быть исчислены на основе сравнения средних темпов роста (или прироста) двух ди­намических рядов за одинаковый период времени:

где Тр", Тр"^п - средние темпы роста первого и второго ря­дов динамики соответственно; я — число лет в периоде.

Коэффициент опережения (отставания) показывает, во сколько раз быстрее растет (отстает) уровень одного ряда динамики по сравнению с другим. При этом сравнении темпы должны характе­ризовать тенденцию одного направления.

7. Методы сглаживания рядов динамики. Одной из важнейших задач статистики является определение в рядах динамики общей тенденции развития явления В некоторых случаях закономерность изменения явления, общая тенденция его развития явно и отчетливо отражается уровнями динамического ряда (уровни на изучаемом периоде непрерывно растут или непрерывно снижаются).Однако часто приходится встречаться с такими рядами ди­намики, в которых уровни ряда претерпевают самые различные изменения (то возрастают, то убывают), и общая тенденция раз­вития неясна.На развитие явления во времени оказывают влияние факто­ры, различные по характеру и силе воздействия. Одни из них оказывают практически постоянное воздействие и формируют в рядах динамики определенную тенденцию развития. Воздействие же других факторов может быть кратковременным или носить случайный характер. Поэтому при анализе динамики речь идет не просто о тен­денции развития, а об основной тенденции, достаточно стабиль­ной (устойчивой) на протяжении изученного этапа развития.

Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний.

Задача состоит в том, чтобы выявить общую тенденцию в изменении уровней ряда, освобожденную от действия различ­ных случайных факторов. С этой целью ряды динамики подвергаются обработке методами укрупнения ин­тервалов, скользящей средней и аналитического выравнивания.

* Одним из наиболее простых методов изучения основной тенденции в рядах динамики является укрупнение интервалов. Он основан на укрупнении периодов времени, к которым отно­сятся уровни ряда динамики (одновременно уменьшается коли­чество интервалов). Например, ряд ежесуточного выпуска про­дукции заменяется рядом месячного выпуска продукции и т.д. Средняя, исчисленная по укрупненным^ интервалам, позволяет выявлять направление и характер (ускорение или замедление роста) основной тенденции развития.

* Выявление основной тенденции может осуществляться также методом скользящи (подвижной) средней. Сущность его заключается в том, что исчисляется средний уровень из опреде­ленного числа, обычно нечетного (3, 5, 7 и т.д.), первыхтю сче­ту уровней ряда, затем — из такого же числа уровней, но начи­ная со второго по счету, далее — начиная с третьего и т.д. Таким образом, средняя как бы «скользит» по ряду динамики, пере­двигаясь на один срок.

на два члена в начале и конце ряда. Он меньше, чем фактиче­ский подвержен колебаниям из-за случайных причин, и четче, в виде некоторой плавной линии на графике, выражает основную тенденцию роста урожайности за изучаемый период, связанную с действием долговременно существующих причин и условий развития.

Недостатком сглаживания ряда является «укорачивание» сглаженного ряда по сравнению с фактическим, а следователь­но, потеря информации.

Рассмотренные приемы сглаживания динамических рядов (укрупнение интервалов и метод скользящей средней) дают воз­можность определить лишь общую тенденцию развития явле­ния, более или менее освобожденную от случайных и волнооб­разных колебаний. Однако получить обобщенную статистиче­скую модель тренда посредством этих методов нельзя.

* Для того чтобы дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во вре­мени, используется аналитическое выравнивание ряда динамики.

Основным содержанием метода аналитического выравнива­ния в рядах динамики является то, что общая тенденция разви­тия рассчитывается как функция времени:

где yt — уровни динамического ряда, вычисленные по соответст­вующему аналитическому уравнению на момент времени t.

Определение теоретических (расчетных) уровней y_t произ­водится на основе так называемой адекватной математической модели, которая наилучшим образом отображает (аппроксимиру­ет) основную тенденцию ряда динамики. Выбор типа модели зависит от цели исследования и должен быть основан на теоретическом анализе, выявляющем характер развития явления, а также на графическом изображении ряда динамики (линейной диаграмме).

Например, простейшими моделями (формулами), выражаю­щими тенденцию развития, являются:

линейная функция — прямая yt = a0 + a1t,

где a0,a1 — параметры уравнения; t — время;

показательная функция yt = A0A_1t

степенная функция - кривая второго порядка (парабола)

В тех случаях, когда требуется особо точное изучение тен­денции развития (например, модели тренда для прогнозирова­ния), при выборе вида адекватной функции можно использовать специальные критерии математической статистики.

Расчет параметров функции обычно производится методом наименьших квадратов, в котором в качестве решения принима­ется точка минимума суммы квадратов отклонений между тео­ретическими и эмпиричесими уровнями:

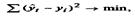
где y_t - выравненные (расчетные) уровни; y_t - фактические уровни.

Параметры уравнения а,-, удовлетворяющие этому условию, могут быть найдены решением системы нормальных уравнений. На основе найденного уравнения тренда вычисляются выравненные уровни. Таким образом, выравнивание ряда динамики заключается в замене фактических уровней у,- плавно изменяю­щимися уровнями У(, наилучшим образом аппроксимирующилми статистические данные.

• Выравнивание по прямой используется, как правило, в тех случаях, когда абсолютные приросты практически постоянны, т. е. когда уровни изменяются в арифметической прогрессии (или близко к ней).

• Выравнивание по показательной функции используется в тех случаях, когда ряд отражает развитие в геометриче­ской прогрессии, т. е. когда цепные коэффициенты рос­та практически постоянны.

Рассмотрим «технику» выравнивания ряда динамики по прямой: yt=a0+a1t

Параметры а0, а1согласно методу наименьших квадратов находятся решением следующей системы нор­мальных уравнений, полученной путем алгебраического преобразования условия

где у - фактические (эмпирические) уровни ряда; t - время (порядковый номеа периода или момента времени).

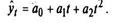
В обоих случаях ∑ t = 0, так что система нормальных урав­нений принимает вид:

Из первого уравнения

Из второго уравнения