Вариация — это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Например, работники фирмы различаются по доходам, затратам времени на работу, росту, весу, любимому занятию в свободное время и т.д. Вариация возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Таким образом, величина каждого варианта объективна. Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не раскрывает строения совокупности, которое весьма существенно для ее познания. Средняя не показывает, как располагаются около нее варианты осредняемого признака, сосредоточены ли они вблизи средней или значительно отклоняются от нее. Средняя величина признака в двух совокупностях может бьпъ одинакрвои, но в одном случае все индивидуальные значения отличаются от нее мало, а в другом — эти отличия велики, т.е. в одном случае вариация признака мала, а в другом - велика, это имеет весьма важное значение для характеристики надежности средней величины. К показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение, коэффициент вариации. Самым элементарным показателем вариации признака является размах вариации R, представляющий собой разность между максимальным и минимальным значениями признака: R=Xmax-Xmin
Среднее линейное отклонение d‾ представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической (при этом всегда предполагают, что среднюю вычитают из варианта: (х - x‾).
Среднее линейное отклонение: для несгруппированных данных d = ∑ | x-x‾| / n
где п — число членов ряда; для сгруппированных данных d ‾ =∑ | x-x‾| f / ∑ f
где ∑f - сумма частот вариационного ряда.
Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных):1) простая дисперсия для несгруппированных данных σ2=∑(X-X‾)2 / n 2)взвешенная дисперсия для вариационного ряда σ2=∑(X-X‾)2 f / ∑f Cвойства дисперсии: 1)если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А, то дисперсия от этого не изменится; 2) если все значения признака уменьшить или увеличить в одно и то же число раз (i раз), то дисперсия соответственно уменьшится или увеличится в i2 раз.Используя второе свойство дисперсии, разделив все варианты на величину интервала, получим следующую формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:

где а — дисперсия, исчисленная по способу моментов; i— величина интервала; x1=x-A/ i новые (преобразованные) значения вариантов
(А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой);
— момент второго порядка;
— квадрат момента первого порядка
Среднее квадратическое отклонение σ равно корню квад-| ратному из дисперсии:
для несгруппированных данных

для вариационного ряда
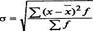
Среднее квадратическое отклонение — это обобщающая характеристика размеров вариации признака в совокупности; оно показывает, на сколько в среднем отклоняются конкретные ва- рианты от их среднего значения; является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, поэтому экономически хорошо интерпретируется.
Обозначим: 1 — наличие интересующего нас признака; 0 — его отсутствие; р — доля единиц, обладающих данным признаком; q — доля единиц, не обладающих данным признаком; р + q =1. Исчислим среднее значение альтернативного признака и его дисперсию. Среднее значение альтернативного признака так как p + q = l.,то







